
家庭值亚 第2课时 比例的其他性质
第2课时 比例的其他性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基出自主梳理 1.如果号=合…b+++0),那么g什牛m b+d+…+n 温馨提示 该性质我们称之为比例的等比性质.比例的性质是比例变形 的重要依据和手段在运用等比性质时,要注意“各分母的和不 为零”的前提条件
基础自主梳理 1.如果𝒂 𝒃 = 𝒄 𝒅 =…= 𝒎 𝒏 (b+d+…+n≠0),那么𝒂+𝒄+…+𝒎 𝒃+𝒅+…+𝒏 = 𝐚 𝐛 . 温馨提示 该性质我们称之为比例的等比性质.比例的性质是比例变形 的重要依据和手段.在运用等比性质时,要注意“各分母的和不 为零”的前提条件

2若号=子,且a+c=4,则+(C1 A.12 B降 D.4 知识拓展 磐=两边同时加或减1时等号不变,即可得结论 =± d 于是我们得到比例的合比性质: 如果8=那么== c-d d 合
2.若 𝒂 𝒃 = 𝒄 𝒅 =3,且 a+c=4,则 b+d=( ). A.12 B. 𝟑 𝟒 C. 𝟒 𝟑 D.4 C 知识拓展 由 𝒂 𝒃 = 𝒄 𝒅 两边同时加或减 1 时等号不变,即可得结论𝒂±𝒃 𝒃 = 𝒄±𝒅 𝒅 , 于是我们得到比例的合比性质: 如果𝒂 𝒃 = 𝒄 𝒅 ,那么𝒂+𝒃 𝒃 = 𝒄+𝒅 𝒅 , 𝒂-𝒃 𝒃 = 𝒄-𝒅 𝒅
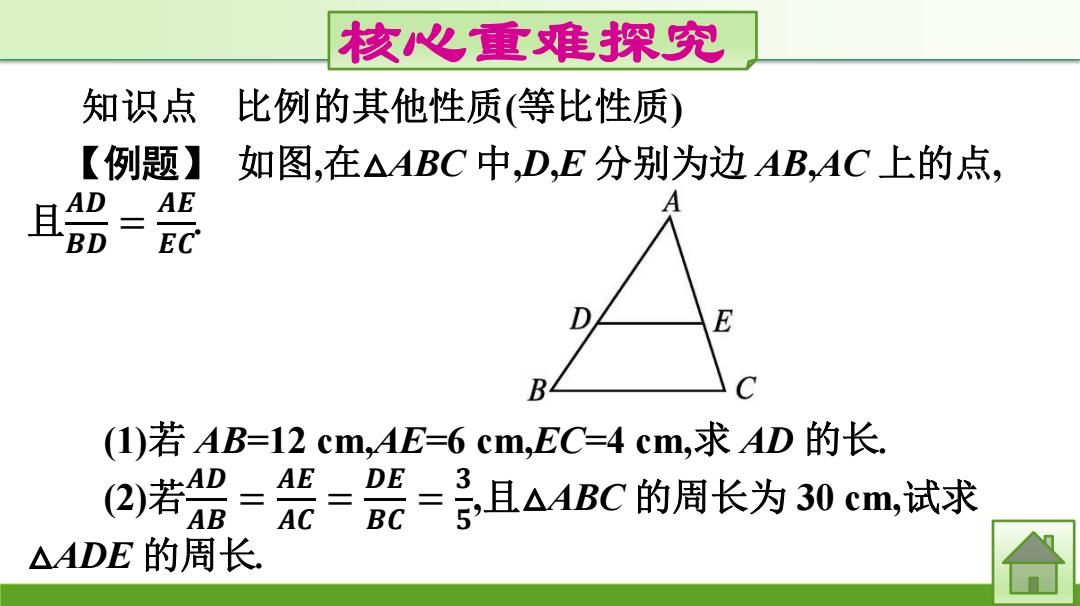
核心重难探究 知识点 比例的其他性质(等比性质) 【例题】 如图,在△ABC中,D,E分别为边AB,AC上的点, 且 AD = EC E B (1)若AB=12cm,AE=6cm,EC=4cm,求AD的长. (2)若 3 AB AC =号,且△ABC的周长为30cm,试求 BC △ADE的周长
核心重难探究 知识点 比例的其他性质(等比性质) 【例题】 如图,在△ABC 中,D,E 分别为边 AB,AC 上的点, 且 𝑨𝑫 𝑩𝑫 = 𝑨𝑬 𝑬𝑪 . (1)若 AB=12 cm,AE=6 cm,EC=4 cm,求 AD 的长. (2)若 𝑨𝑫 𝑨𝑩 = 𝑨𝑬 𝑨𝑪 = 𝑫𝑬 𝑩𝑪 = 𝟑 𝟓 ,且△ABC 的周长为 30 cm,试求 △ADE 的周长

思路点拨:)选AD为未知量,根据已知比例式可列方程求解; (2)直接利用比例的等比性质易于获解 解:)淡ADcm,根据意意,得=系鲜得 =7.2. 径检验,x=7.2是原方程的解,即AD的长为7.2cm. (2由比例的等比性质,得A0+A+P= AB+AC+BC 所以△ADE的周长为×30=18(cm
思路点拨:(1)选AD为未知量,根据已知比例式可列方程求解; (2)直接利用比例的等比性质易于获解. 解:(1)设 AD=x cm,根据题意,得 𝐱 𝟏𝟐-𝐱 = 𝟔 𝟒 ,解得 x=7.2. 经检验,x=7.2 是原方程的解,即 AD 的长为 7.2 cm. (2)由比例的等比性质,得 𝐀𝐃+𝐀𝐄+𝐃𝐄 𝐀𝐁+𝐀𝐂+𝐁𝐂 = 𝟑 𝟓 . 所以△ADE 的周长为𝟑 𝟓 ×30=18(cm)

【方法归纳】 成比例线段与比例的性质是进行线段求值问题的重要依据 与途径根据比例的性质,得到如下结论: 如果号=那么=b±0)也成立 合
【方法归纳】 成比例线段与比例的性质是进行线段求值问题的重要依据 与途径.根据比例的性质,得到如下结论: 如果𝒂 𝒃 = 𝒄 𝒅 ,那么𝒂±𝒄 𝒃±𝒅 = 𝒂 𝒃 (b±d≠0)也成立

新知训川练巩固 1.若 成立,则下列式子一定成立的是(D1 a+1 c+1 ac A -1 d+1 B. C d a D.ad=bc 2.若 =月=6+d40.则(+)》= = 3己知号==号=则2(+)= (b+0);若-c+e=10,则 b-d+f
新知训练巩固 1.若 𝒂 𝒃 = 𝒄 𝒅 成立,则下列式子一定成立的是( ). A. 𝒂+𝟏 𝒃+𝟏 = 𝒄+𝟏 𝒅+𝟏 B. 𝒂𝒄 𝒃𝒄 = 𝒄 𝟐 𝒅𝒄 C. 𝒃 𝒂 = 𝒅 𝒄 D.ad=bc 2.若 𝒂 𝒃 = 𝒄 𝒅 = 𝒆 𝒇 = 𝟑 𝟒 (b+d+f≠0),则 𝒂+𝒄+𝒆 𝒃+𝒅+𝒇 𝟐 = 𝟗 𝟏𝟔 . 3.已知𝒂 𝒃 = 𝒄 𝒅 = 𝒆 𝒇 = 𝟐 𝟑 ,则 2 𝒂+𝒆 𝒃+𝒇 = 𝟒 𝟑 (b+f≠0);若 a-c+e=10,则 b-d+f=15 . D

4已知a6c为△ABC的三边,且tb+-60,g冬写试求 △ABC的面积 解:由比例性质,得号== a+b+c 6 3+4+5 0=5, 1 ∴.a=15,b=20,c=25.又152+202=252, 即a2+b2=c2,∴.△ABC是直角三角形, ∴.S△ABc=15×20÷2=150
4.已知a,b,c为△ABC的三边,且a+b+c=60, ,试求 △ABC的面积. 𝒂 𝟑 = 𝒃 𝟒 = 𝒄 𝟓 解:由比例性质,得 𝐚 𝟑 = 𝐛 𝟒 = 𝐜 𝟓 = 𝐚+𝐛+𝐜 𝟑+𝟒+𝟓 = 𝟔𝟎 𝟏𝟐 =5, ∴a=15,b=20,c=25.又152+202=252 , 即a 2+b2=c2 ,∴△ABC是直角三角形, ∴S△ABC=15×20÷2=150

素能演练提升 1.已知 b+c += 5 6 则a+h+c的值为D人 2 A 2 B. 3 C.12 D.6 2.已知+也 b+c c+a 15 17 16 则a.bc=(A) A.78.9 B.987 C.87.9 D.9.7.8 3若=号=台设4x++t0,BC-Y则4,B,C 的大小顺序为(B) A.A>B>C B.AA>B D.A<C<B
素能演练提升 1.已知𝒂+𝒃 𝟓 = 𝒃+𝒄 𝟔 = 𝒄+𝒂 𝟕 = 𝟐 𝟑 ,则 a+b+c 的值为( ). A. 𝟐 𝟐𝟕 B. 𝟐 𝟑 C.12 D.6 2.已知𝒂+𝒃 𝟏𝟓 = 𝒃+𝒄 𝟏𝟕 = 𝒄+𝒂 𝟏𝟔 ,则 a∶b∶c=( ). A.7∶8∶9 B.9∶8∶7 C.8∶7∶9 D.9∶7∶8 3.若 𝒙 𝟐 = 𝒚 𝟕 = 𝒛 𝟓 ,设 A= 𝒚 𝒙+𝒚+𝒛 (x+y+z≠0),B=𝒙+𝒛 𝒚 ,C=𝒙+𝒚-𝒛 𝒙 ,则 A,B,C 的大小顺序为( ). A.A>B>C B.AA>B D.A<C<B D A B