
家庭猴伞 第2课时 估算一元二次方程的近以解
第2课时 估算一元二次方程的近似解

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基出自主梳理 1.使一元二次方程x2+bx+c=0(呋0)的左、右两边 的 未知数x的值,叫做这个一元二次方程的解,也称为这个一元二 次方程的根. 2.若关于x的一元二次方程x2+px-2=0的一个根为2,则侧p的值 为(C). A.1 B.2 C.-1 D.-2 3.对一元二次方程解的估算,应先根据实际确定它的解的大 致..,再通过具体代值计算进行两边“夹逼”,逐步求得其 解的近似值
基础自主梳理 1.使一元二次方程ax2+bx+c=0(a≠0)的左、右两边相等 的 未知数x的值,叫做这个一元二次方程的解,也称为这个一元二 次方程的根. 2.若关于x的一元二次方程x 2+px-2=0的一个根为2,则p的值 为( ). A.1 B.2 C.-1 D.-2 3.对一元二次方程解的估算,应先根据实际确定它的解的大 致范围 ,再通过具体代值计算进行两边“夹逼”,逐步求得其 解的近似值. C

温馨提示 与估算一个无理数(如2)的近似值类似,我们通常采用“夹 逼法”估算一元二次方程的近似解.估计一元二次方程的解,只 是估计“解”的取值范围,比如在哪两个数之间.当相邻的两个 数,一个使x2+bx+c0(0)时,则关 于x的一元二次方程x2+bx+c=0(0)的解就介于这两个数之 间.认真观察代数式x2+bx+c(呋0)的特点和取值走向,就能很 快地找到这样相邻的两个数
温馨提示 与估算一个无理数(如 )的近似值类似,我们通常采用“夹 逼法”估算一元二次方程的近似解.估计一元二次方程的解,只 是估计“解”的取值范围,比如在哪两个数之间.当相邻的两个 数,一个使ax2+bx+c0(a≠0)时,则关 于x的一元二次方程ax2+bx+c=0(a≠0)的解就介于这两个数之 间.认真观察代数式ax2+bx+c(a≠0)的特点和取值走向,就能很 快地找到这样相邻的两个数. 𝟐

核心重难探究 知识点 估算一元二次方程的近似解 【例题】写出一个一元二次方程,使其二次项系数为1,一次 项系数为-2,常数项为-4,并求出该方程的近似解精确到个位) 思路点拨:先根据题意列出方程,再列表求值进行“夹逼”,进 而确定方程的近似解
核心重难探究 知识点 估算一元二次方程的近似解 【例题】写出一个一元二次方程,使其二次项系数为1,一次 项系数为-2,常数项为-4,并求出该方程的近似解.(精确到个位) 思路点拨:先根据题意列出方程,再列表求值进行“夹逼”,进 而确定方程的近似解

解:一元二次方程为x2-2x-4=0. 根据方程可列表如下: 4 -4 3 2 -1 0 1 2 3 4 x2.2x-4 20 11 4 1 4 5 4 1 4 ∴.方程的解应在-2到-1或3到4之间. 因此再列表计算: 1.4 1.3 -1.2 -1.1 3.1 3.2 3.3 3.4 x2-2x-40.76 0.29 -0.16 -0.59 -0.59 -0.16 0.29 0.76 .方程的解为x≈-1或x≈3
解:一元二次方程为x 2 -2x-4=0. 根据方程可列表如下: x -4 -3 -2 -1 0 1 2 3 4 x 2 -2x-4 20 11 4 -1 -4 -5 -4 -1 4 ∴方程的解应在-2到-1或3到4之间. 因此再列表计算: x -1.4 -1.3 -1.2 -1.1 3.1 3.2 3.3 3.4 x 2 -2x-4 0.76 0.29 -0.16 -0.59 -0.59 -0.16 0.29 0.76 ∴方程的解为x≈-1或x≈3

【方法归纳】 利用列表法估算关于x的一元二次方程x2+bx+c=O(≠0)近 似解的步骤: ()将方程化为一般形式; (2)根据实际情况确定方程解的大致范围; (3)列表,分别计算ax2+bx+c的值; (4)在表中找出当x2+bx+c的值可能等于0的未知数的范围; (⑤)进一步在(4)的范围内列表、计算、估计范围,直到找出 符合要求的解
【方法归纳】 利用列表法估算关于x的一元二次方程ax2+bx+c=0(a≠0)近 似解的步骤: (1)将方程化为一般形式; (2)根据实际情况确定方程解的大致范围; (3)列表,分别计算ax2+bx+c的值; (4)在表中找出当ax2+bx+c的值可能等于0的未知数的范围; (5)进一步在(4)的范围内列表、计算、估计范围,直到找出 符合要求的解
新知川练织固 1输入一组数据,按下列程序进行计算,输出结果如下表: 输入x +8 平方 -826 输出 比 20.5 20.6 20.7 20.8 20.9 输出 13.75 -8.04 -2.31 3.44 9.21
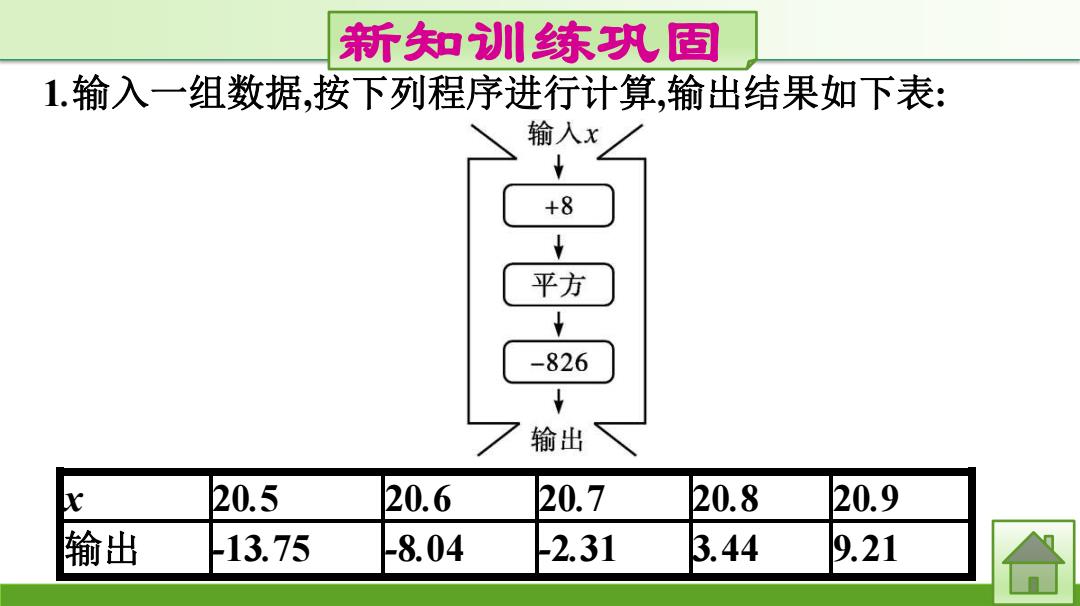
新知训练巩固 1.输入一组数据,按下列程序进行计算,输出结果如下表: x 20.5 20.6 20.7 20.8 20.9 输出 -13.75 -8.04 -2.31 3.44 9.21

分析表格中的数据,估计方程x+8)2-826=0的一个正数解x的 大致范围为(C). A.20.5<x<20.6 B.20.6<x<20.7 C.20.7<x<20.8 D.20.8<x<20.9
分析表格中的数据,估计方程(x+8)2 -826=0的一个正数解x的 大致范围为( ). A.20.5<x<20.6 B.20.6<x<20.7 C.20.7<x<20.8 D.20.8<x<20.9 C

2.已知实数a是一元二次方程x2-1016x+1=0的根,则代数式2- a2+1 1015-1016 的值为 合
2.已知实数a是一元二次方程x 2 -1 016x+1=0的根,则代数式a 2 - 1 015a- 的值为-1 . 𝒂 𝟐 + 𝟏 𝟏 𝟎𝟏𝟔