
家庭猴伞 第1课时 应用一元二次方程解快几何问题
第1课时 应用一元二次方程解决几何问题

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.列一元二次方程解应用题的一般步骤 审:读懂题目,弄清题意,明确哪些是已知量,哪些是未知量,以 及它们之间的等量关系; 设:设元,也就是设未知数,主要有直接设元法与间接设元法, 因题而异; 列:列方程,一般先找出能够表达应用题全部含义的一个等 量关系,再列代数式表示相等关系中的各个量,即得方程; 解:解方程,求出未知数的值; 验:检验方程的解能否保证实际问题有意义; 答:作答
基础自主梳理 1.列一元二次方程解应用题的一般步骤 审:读懂题目,弄清题意,明确哪些是已知量,哪些是未知量,以 及它们之间的等量关系; 设:设元,也就是设未知数,主要有直接设元法与间接设元法, 因题而异; 列:列方程,一般先找出能够表达应用题全部含义的一个等 量关系,再列代数式表示相等关系中的各个量,即得方程; 解:解方程,求出未知数的值; 验:检验方程的解能否保证实际问题有意义; 答:作答

2.如图,某幼儿园有一面长为16m的墙,计划用32m长的围 栏靠墙围成一个面积为120m的矩形草坪ABCD,则该矩形草 坪BC边的长为 m. 16m A 草坪 B C
2.如图,某幼儿园有一面长为16 m的墙,计划用32 m长的围 栏靠墙围成一个面积为120 m2的矩形草坪ABCD,则该矩形草 坪BC边的长为12 m
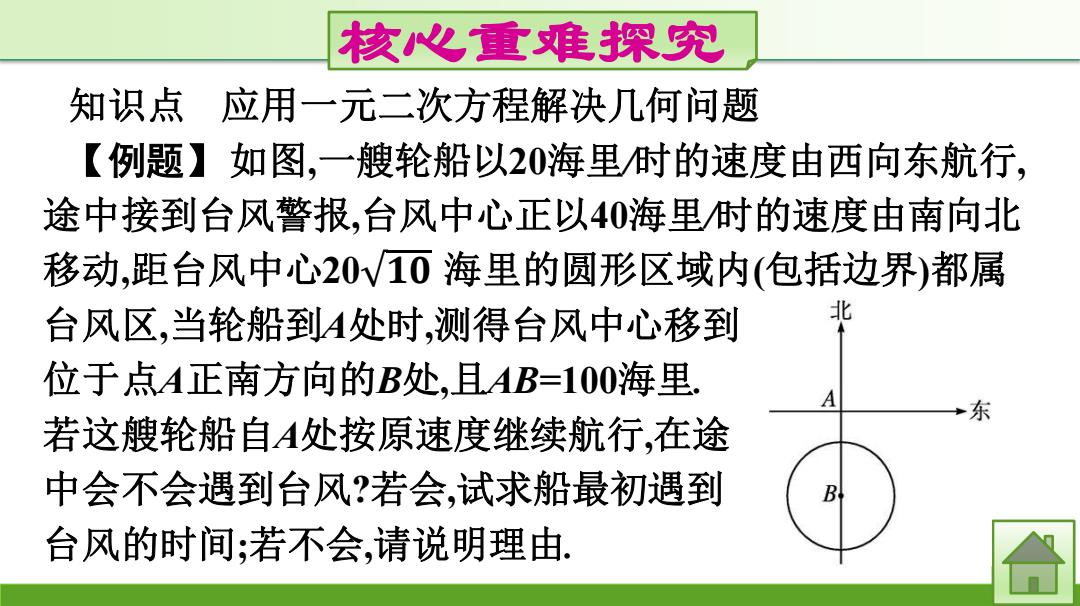
核心重难探究 知识点 应用一元二次方程解决几何问题 【例题】如图,一艘轮船以20海里付的速度由西向东航行, 途中接到台风警报,台风中心正以40海里时的速度由南向北 移动,距台风中心20v10海里的圆形区域内(包括边界)都属 台风区,当轮船到4处时,测得台风中心移到 北 位于点A正南方向的B处,且AB=100海里 A +东 若这艘轮船自A处按原速度继续航行,在途 中会不会遇到台风?若会,试求船最初遇到 B 台风的时间;若不会,请说明理由
核心重难探究 知识点 应用一元二次方程解决几何问题 【例题】如图,一艘轮船以20海里/时的速度由西向东航行, 途中接到台风警报,台风中心正以40海里/时的速度由南向北 移动,距台风中心 海里的圆形区域内(包括边界)都属 台风区,当轮船到A处时,测得台风中心移到 位于点A正南方向的B处,且AB=100海里. 若这艘轮船自A处按原速度继续航行,在途 中会不会遇到台风?若会,试求船最初遇到 台风的时间;若不会,请说明理由. 20 𝟏𝟎

思路点拨:先假设会遇到台风,用关于时间的代数式分别表 示参考答案图中AE,AC的长度,再利用勾股定理列出方程,如 果这个方程有符合题意的正数解,说明会遇到台风,否则不会 遇到台风
思路点拨:先假设会遇到台风,用关于时间t的代数式分别表 示参考答案图中AE,AC的长度,再利用勾股定理列出方程,如 果这个方程有符合题意的正数解,说明会遇到台风,否则不会 遇到台风

解:设途中会遇到台风,且最初遇到台风的时间为轮船自A处 航行t小时时,此时轮船位于C处,台风中心移到E处, 连接CE(如图),则有AC=20t,BE=40t,EC=20V10. 北 '.AE=AB-BE=100-40t 在Rt△AEC中,AC2+AE2=EC2, A 东 ∴.(20t)2+(100-40t)2=(20V10)2. 整理,得24+3=0,解得t=1,t2=3. '途中会遇到台风,且最初遇到台风的时间为轮船自A处航 行1小时时
解:设途中会遇到台风,且最初遇到台风的时间为轮船自A处 航行t小时时,此时轮船位于C处,台风中心移到E处, 连接 CE(如图),则有 AC=20t,BE=40t,EC=20 𝟏𝟎. ∴AE=AB-BE=100-40t. 在 Rt△AEC 中,AC2 +AE2 =EC2 , ∴(20t)2 +(100-40t)2 =(20 𝟏𝟎) 2 . 整理,得 t 2 -4t+3=0,解得 t1=1,t2=3. ∴途中会遇到台风,且最初遇到台风的时间为轮船自A处航 行1小时时

【方法归纳】 在直角三角形中,如果三边的长度可以用只含一个未知数的 代数式来表示,或者某条边的长度可以求出,那么就可以利用 勾股定理来列一元二次方程求解,这是一种常用的解题方法
【方法归纳】 在直角三角形中,如果三边的长度可以用只含一个未知数的 代数式来表示,或者某条边的长度可以求出,那么就可以利用 勾股定理来列一元二次方程求解,这是一种常用的解题方法
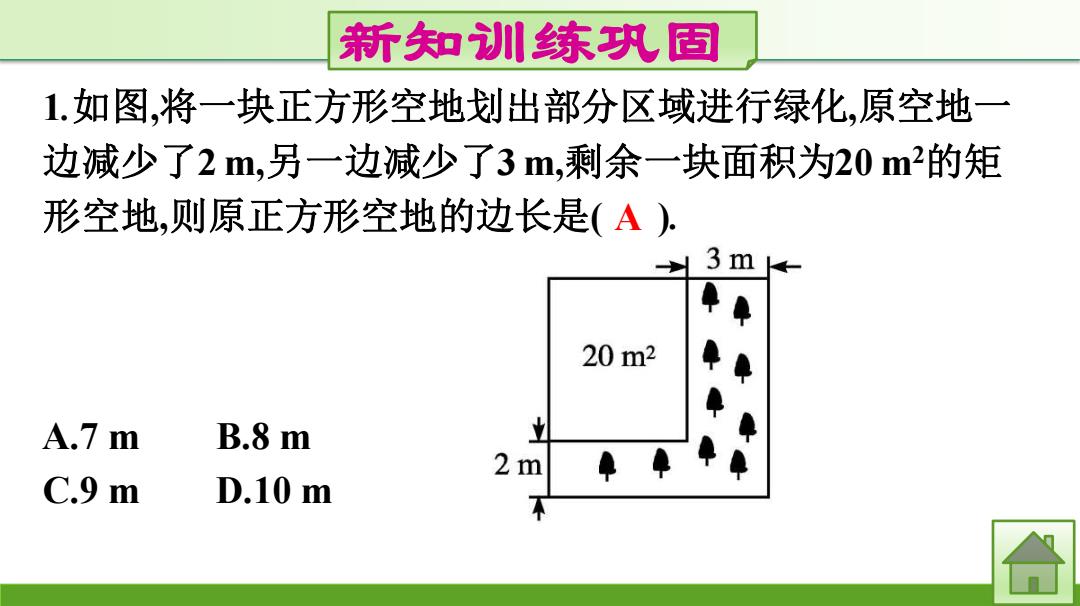
新知训川练织固 1.如图,将一块正方形空地划出部分区域进行绿化,原空地一 边减少了2m,另一边减少了3m,剩余一块面积为20m的矩 形空地,则原正方形空地的边长是(A) 3m 20m2 A.7 m B.8 m 2 m C.9 m D.10m
新知训练巩固 1.如图,将一块正方形空地划出部分区域进行绿化,原空地一 边减少了2 m,另一边减少了3 m,剩余一块面积为20 m2的矩 形空地,则原正方形空地的边长是( ). A.7 m B.8 m C.9 m D.10 m A
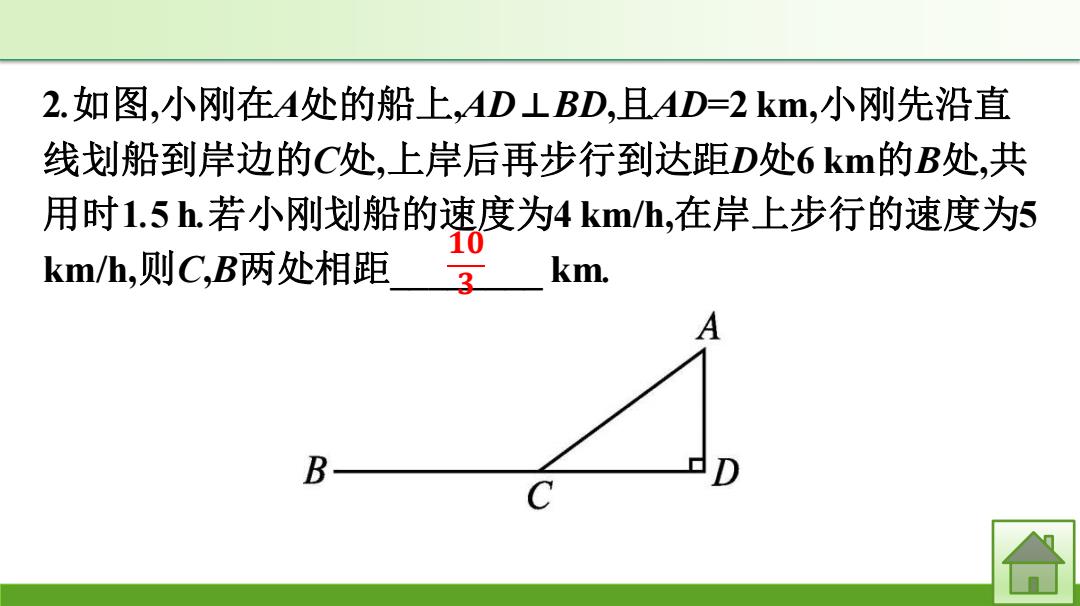
2.如图,小刚在A处的船上,AD LBD,且AD=2km,小刚先沿直 线划船到岸边的C处,上岸后再步行到达距D处6km的B处,共 用时1.5h.若小刚划船的速度为4km/h,在岸上步行的速度为5 10 km/h,则C,B两处相距 3 km. A B 合
2.如图,小刚在A处的船上,AD⊥BD,且AD=2 km,小刚先沿直 线划船到岸边的C处,上岸后再步行到达距D处6 km的B处,共 用时1.5 h.若小刚划船的速度为4 km/h,在岸上步行的速度为5 km/h,则C,B两处相距________ km. 𝟏𝟎 𝟑