
家庭值四 6 利用相以三确形测高
6 利用相似三角形测高

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基出自主梳理 1.利用相似三角形测量旗杆高度的方法 (1)利用阳光下的 (2)利用 3)利用镜子的 合
基础自主梳理 1.利用相似三角形测量旗杆高度的方法 (1)利用阳光下的影子 ; (2)利用标杆 ; (3)利用镜子的反射

名师指导 方法(1)的原理是同一时刻物高与影长成比例;方法(2)的原 理是构造相似三角形,把被测物体分成两部分求解,使用这种 方法时,注意人眼、标杆顶端和被测物体的顶端三点要共线, 即人眼恰好看不见被测物体;方法(3)的原理是利用“入射角等 于反射角”的物理知识构造相似三角形求解
名师指导 方法(1)的原理是同一时刻物高与影长成比例;方法(2)的原 理是构造相似三角形,把被测物体分成两部分求解,使用这种 方法时,注意人眼、标杆顶端和被测物体的顶端三点要共线, 即人眼恰好看不见被测物体;方法(3)的原理是利用“入射角等 于反射角”的物理知识构造相似三角形求解
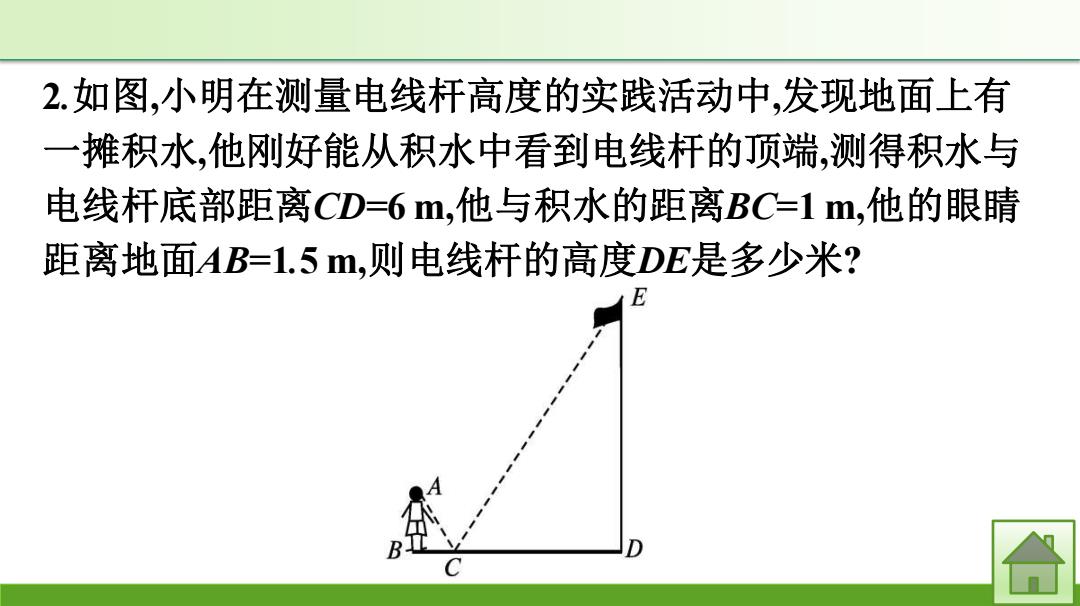
2.如图,小明在测量电线杆高度的实践活动中,发现地面上有 一摊积水,他刚好能从积水中看到电线杆的顶端,测得积水与 电线杆底部距离CD=6m,他与积水的距离BC=1m,他的眼睛 距离地面AB=1.5m,则电线杆的高度DE是多少米?
2.如图,小明在测量电线杆高度的实践活动中,发现地面上有 一摊积水,他刚好能从积水中看到电线杆的顶端,测得积水与 电线杆底部距离CD=6 m,他与积水的距离BC=1 m,他的眼睛 距离地面AB=1.5 m,则电线杆的高度DE是多少米?

解:由题意可知∠ABC=∠EDC=90°,∠ACB=∠ECD, △ABC∽AEDC,S BC DC .'CD=6 m,BC=1 m,AB=1.5 m, 。1.5 =名DE=9m ED
解:由题意可知∠ABC=∠EDC=90°,∠ACB=∠ECD, ∴△ABC∽△EDC,∴ 𝐀𝐁 𝐄𝐃 = 𝐁𝐂 𝐃𝐂 . ∵CD=6 m,BC=1 m,AB=1.5 m, ∴ 𝟏.𝟓 𝐄𝐃 = 𝟏 𝟔 ,∴DE=9 m
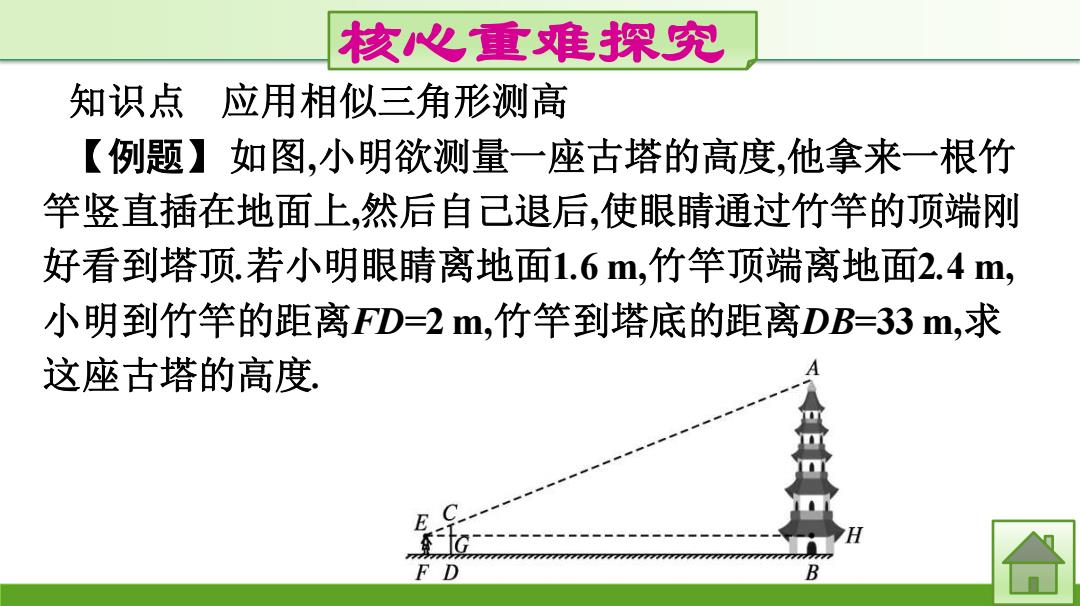
核心重难探究 知识点 应用相似三角形测高 【例题】如图,小明欲测量一座古塔的高度,他拿来一根竹 竿竖直插在地面上,然后自己退后,使眼睛通过竹竿的顶端刚 好看到塔顶.若小明眼睛离地面1.6m,竹竿顶端离地面2.4m, 小明到竹竿的距离FD=2m,竹竿到塔底的距离DB=33,求 这座古塔的高度! B
核心重难探究 知识点 应用相似三角形测高 【例题】如图,小明欲测量一座古塔的高度,他拿来一根竹 竿竖直插在地面上,然后自己退后,使眼睛通过竹竿的顶端刚 好看到塔顶.若小明眼睛离地面1.6 m,竹竿顶端离地面2.4 m, 小明到竹竿的距离FD=2 m,竹竿到塔底的距离DB=33 m,求 这座古塔的高度

思路点拨:(1)图中线段CG的长是多少?塔高AB等于哪两条 线段的和? 2)△EGC与△EHA相似吗?为什么? 合
思路点拨:(1)图中线段CG的长是多少?塔高AB等于哪两条 线段的和? (2)△EGC与△EHA相似吗?为什么?

解:,'小明、竹竿、古塔均与地面垂直,EH⊥AB, .'BH=DG=EF=1.6 m,EG=DF,GH=DB. 小明眼睛离地面1.6m,竹竿项端离地面2.4m, '.CG=CD-EF=2.4-1.6=0.8(m). ,'CDIIAB,,△EGC~△EHA. 。AHI 即A= CG EG' T0.8 轻,解得AH14m .'.AB=AH+BH=14+1.6=15.6(m). 答:古搭的高度是15.6m. 合
解:∵小明、竹竿、古塔均与地面垂直,EH⊥AB, ∴BH=DG=EF=1.6 m,EG=DF,GH=DB. ∵小明眼睛离地面1.6 m,竹竿顶端离地面2.4 m, ∴CG=CD-EF=2.4-1.6=0.8(m). ∵CD∥AB,∴△EGC∽△EHA. ∴ 𝐀𝐇 𝐂𝐆 = 𝐄𝐇 𝐄𝐆 ,即 𝐀𝐇 𝟎.𝟖 = 𝟑𝟑+𝟐 𝟐 ,解得 AH=14 m. ∴AB=AH+BH=14+1.6=15.6(m). 答:古塔的高度是15.6 m

【方法归纳】 1.借助标杆来测量物体的高度的一般思路是:从人眼所在的 位置向物体作垂线,根据人、标杆、物体都与地面垂直构造 相似三角形这一数学模型,结合相似三角形对应边成比例求 解 2.利用三角形相似解决实际问题的一般步骤:(1)根据题意画 出示意图;2)将题目中的已知量或已知关系转化为示意图中 的已知线段或角;3)利用相似三角形建立线段之间的关系,求 出未知量;(4)写出答案
【方法归纳】 1.借助标杆来测量物体的高度的一般思路是:从人眼所在的 位置向物体作垂线,根据人、标杆、物体都与地面垂直构造 相似三角形这一数学模型,结合相似三角形对应边成比例求 解. 2.利用三角形相似解决实际问题的一般步骤:(1)根据题意画 出示意图;(2)将题目中的已知量或已知关系转化为示意图中 的已知线段或角;(3)利用相似三角形建立线段之间的关系,求 出未知量;(4)写出答案