
家庭们亚 5】 三角函数的应用 第1课时 方向角
5 三角函数的应用 第1课时 方向角

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
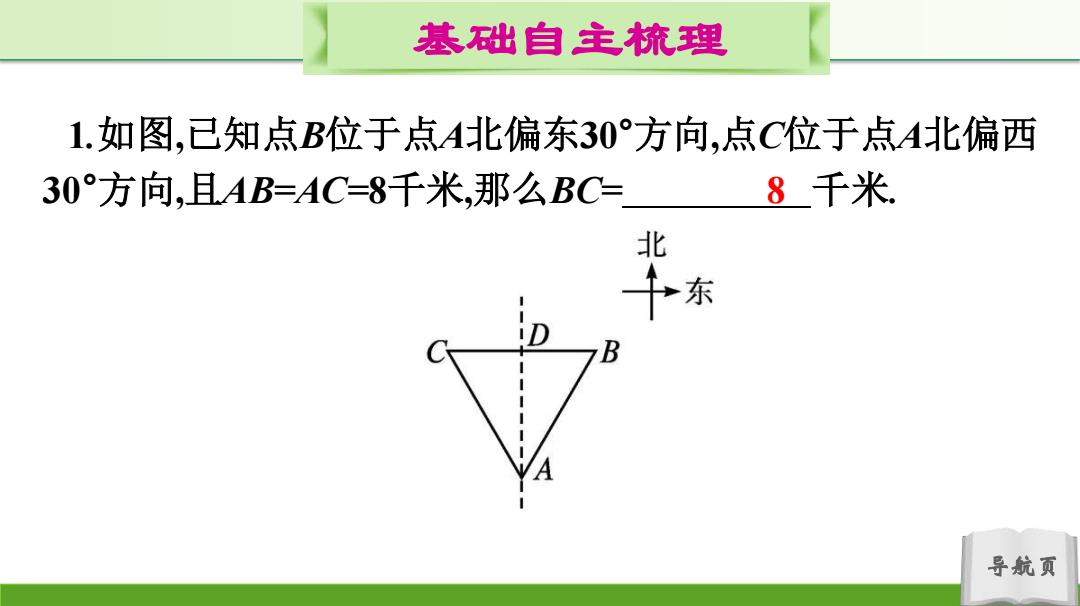
基础自主梳理 1.如图,已知点B位于点A北偏东30°方向,点C位于点A北偏西 30°方向,且AB=AC=8千米,那么BC= 8千米 北 东 导航页
导航页 基础自主梳理 1.如图,已知点B位于点A北偏东30°方向,点C位于点A北偏西 30°方向,且AB=AC=8千米,那么BC= 8 千米

基础自主梳理 2.如图,小明从A处出发,要到北偏东60°方向的C处,他先沿正 东方向走了200米到达B处,再沿北偏东30°方向走恰好能到达 目的地C处则B,C两地的距离为 200米 牛东 60° 396 导航页
导航页 基础自主梳理 2.如图,小明从A处出发,要到北偏东60°方向的C处,他先沿正 东方向走了200米到达B处,再沿北偏东30°方向走恰好能到达 目的地C处.则B,C两地的距离为 200米

核心重难探究 知识点一:求路程问题 【例1】如图,一艘海监船在某岛附近海域 北 巡航,某一时刻海监船在A处测得该岛上某一 东 目标C在它的北偏东45°方向,海监船沿北偏 西30°方向航行60海里后到达B处,此时测得 北 该目标C在它的南偏东75°方向,求此时该船 东 与目标C之间的距离CB的长度.(结果保留根号) 思路点拨:(1)利用BC所在的△ABC能否直接求出BC的长? (2)怎样构造直角三角形求解? 导航页
导航页 核心重难探究 知识点一:求路程问题 【例1】如图,一艘海监船在某岛附近海域 巡航,某一时刻海监船在A处测得该岛上某一 目标C在它的北偏东45°方向,海监船沿北偏 西30°方向航行60海里后到达B处,此时测得 该目标C在它的南偏东75°方向,求此时该船 与目标C之间的距离CB的长度.(结果保留根号) 思路点拨:(1)利用BC所在的△ABC能否直接求出BC的长? (2)怎样构造直角三角形求解?

核心重难探究 解:由题意,得∠EBA=∠FAB=30°, .∴.∠ABC=∠EBC-∠EBA=75°-30°=45°. 北 ..∠C=180°-45°-75°=60°. B 东 D 过点A作AD⊥BC于点D, 则BD=AD=AB:sin∠ABD=60×30V2, 东 CD-AD =3 0Z-10N6. tanC .CB=BD+CD=30v2+10V6)海里. '.该船与岛上目标C之间的距离为(30V2+10V6)海里. 导航页
导航页 核心重难探究 解:由题意,得∠EBA=∠FAB=30° , ∴∠ABC=∠EBC-∠EBA=75°-30° =45° . ∴∠C=180°-45°-75° =60° . 过点A作AD⊥BC于点D, 则 BD=AD=AB·sin∠ABD=60× 𝟐 𝟐 =30 𝟐, CD= 𝑨𝑫 𝐭𝐚𝐧𝑪 = 𝟑𝟎 𝟐 𝟑 =10 𝟔. ∴CB=BD+CD=(30 𝟐+10 𝟔)海里. ∴该船与岛上目标 C 之间的距离为(30 𝟐+10 𝟔)海里

核心重难探究 【方法归纳】 在解决有关方向角的问题中,一般要根据题意理清图形中各 角的关系,有时所给的方向角并不一定在直角三角形中,需要 用到两直线平行内错角相等或两个角互余等知识转化为所需 要的角 导航页
导航页 核心重难探究 【方法归纳】 在解决有关方向角的问题中,一般要根据题意理清图形中各 角的关系,有时所给的方向角并不一定在直角三角形中,需要 用到两直线平行内错角相等或两个角互余等知识转化为所需 要的角

核心重难探究 知识点二:求时间问题 【例2】如图,一巡逻艇在A处执行任务时,发 现在A处的北偏东30°方向有一岛屿C,在A处的 B东 西AE东 北偏东75方向、相距60海里的B处有一不明 南 船只,正以15海里时的速度向位于B处西北方向的C岛航行, 于是巡逻艇马上以20海里时的速度开向C岛去拦截,问巡逻 艇与不明船只谁先到达C岛?(参考数据:v2≈1.4,V3≈1.7) 思路点拨:)怎样构造直角三角形才能利用上两个已知角? (2)利用什么来比较谁先到达C岛? 导航页
导航页 核心重难探究 知识点二:求时间问题 【例2】如图,一巡逻艇在A处执行任务时,发 现在A处的北偏东30°方向有一岛屿C,在A处的 北偏东75°方向、相距60海里的B处有一不明 船只,正以15海里/时的速度向位于B处西北方向的C岛航行, 于是巡逻艇马上以20海里/时的速度开向C岛去拦截,问巡逻 艇与不明船只谁先到达C岛?(参考数据: ≈1.4, ≈1.7) 思路点拨:(1)怎样构造直角三角形才能利用上两个已知角? (2)利用什么来比较谁先到达C岛? 𝟐 𝟑

核心重难探究 解:如图,过点C作CH⊥AB于点H, 由题可得,∠DAB=75°,∠DAC=30°,∠CBF=45°. ∴.∠BAC=45°,∠BAE=∠ABF=15°.∴.∠ABC=60°. 设BH=x海里,则CH=AH=V3x,BC=2x G .AB=60,∴.V3x+x=60, 解得x=30(√3-1). 东 H 西AE东 南 ∴.BH=303-1),AH=30(3-V3), 南 导航页
导航页 核心重难探究 解:如图,过点C作CH⊥AB于点H, 由题可得,∠DAB=75° ,∠DAC=30° ,∠CBF=45° . ∴∠BAC=45° ,∠BAE=∠ABF=15° .∴∠ABC=60° . 设 BH=x 海里,则 CH=AH= 𝟑x,BC=2x. ∵AB=60,∴ 𝟑x+x=60, 解得 x=30( 𝟑-1). ∴BH=30( 𝟑-1),AH=30(3- 𝟑)

核心重难探究 在Rt△ACH中,AC=V2AH=V2×30(3-V3)=30V2(3-V3). 在Rt△BCH中,BC=2BH=60(V3-1). 则巡逻艇到达C岛所用的时间为30V2(3-V3)÷20≈2.7(小时), 不明船只到达C岛所用的时间为60(3-1)÷15≈2.8(小时) 2.8>2.7,.巡逻艇先到达C岛. 【方法归纳】 解决这类问题关键是在不破坏已知角的情况下构造直角三 角形,正确利用勾股定理和三角函数求解 导航页
导航页 核心重难探究 在 Rt△ACH 中,AC= 𝟐AH= 𝟐×30(3- 𝟑)=30 𝟐(3- 𝟑). 在 Rt△BCH 中,BC=2BH=60( 𝟑-1). 则巡逻艇到达 C 岛所用的时间为 30 𝟐(3- 𝟑)÷20≈2.7(小时), 不明船只到达 C 岛所用的时间为 60( 𝟑-1)÷15≈2.8(小时). 2.8>2.7,∴巡逻艇先到达 C 岛. 【方法归纳】 解决这类问题关键是在不破坏已知角的情况下构造直角三 角形,正确利用勾股定理和三角函数求解