
家庭值四 1 锐角三角区数 第1课时 正勿
1 锐角三角函数 第1课时 正切

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
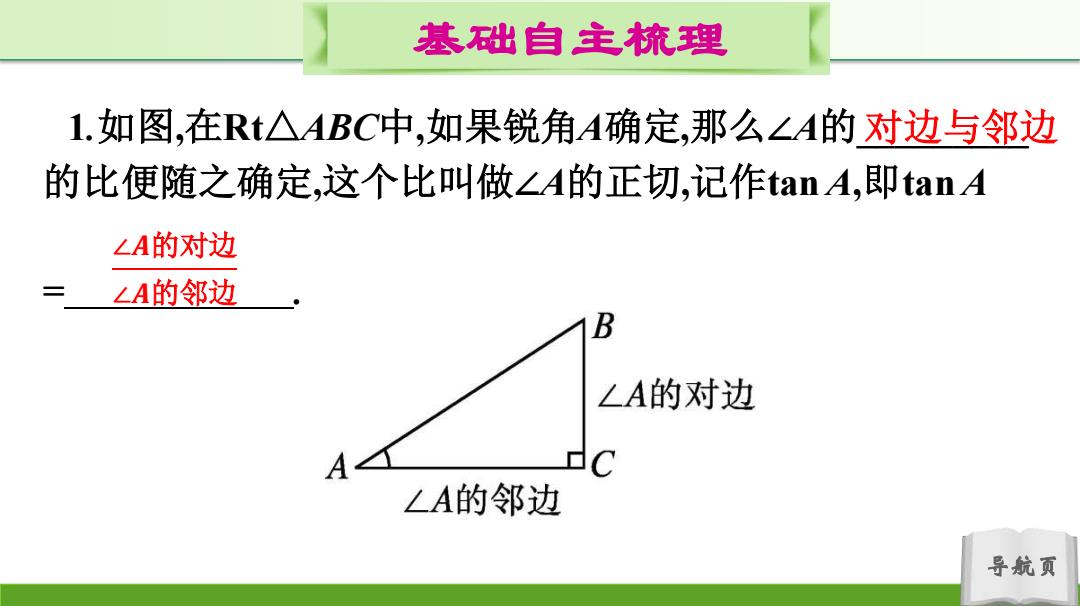
基础自主梳理 1.如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边 的比便随之确定,这个比叫做∠A的正切,记作tanA,即tanA LA的对边 LA的邻边 B ∠A的对边 C ∠A的邻边 导航页
导航页 基础自主梳理 1.如图,在Rt△ABC中,如果锐角A确定,那么∠A的_________ 的比便随之确定,这个比叫做∠A的正切,记作tan A,即tan A = . 对边与邻边 ∠𝑨的对边 ∠𝑨的邻边

基础自主梳理 温馨提示 1.tanA是一个完整的符号,它表示∠A的正切,记号里习惯省 去角的符号“∠.tanA不能写成tanA,也不能理解成tan与∠A 的乘积 2.对三个大写字母表示成的角(如∠ABC),其正切应写成 tan∠ABC,不能写成tan ABC.同样地,tan∠1也不能写成tan1. 3.tan A.tan A=(tanA)2,(tanA2常写成tanA,而不能写成tan A2. 导航页
导航页 基础自主梳理 温馨提示 1.tan A是一个完整的符号,它表示∠A的正切,记号里习惯省 去角的符号“∠” .tanA不能写成tan·A,也不能理解成tan与∠A 的乘积. 2.对三个大写字母表示成的角(如∠ABC),其正切应写成 tan∠ABC,不能写成tanABC.同样地,tan∠1也不能写成tan 1. 3.tan A·tan A=(tan A) 2 ,(tan A) 2常写成tan2A,而不能写成tan A2
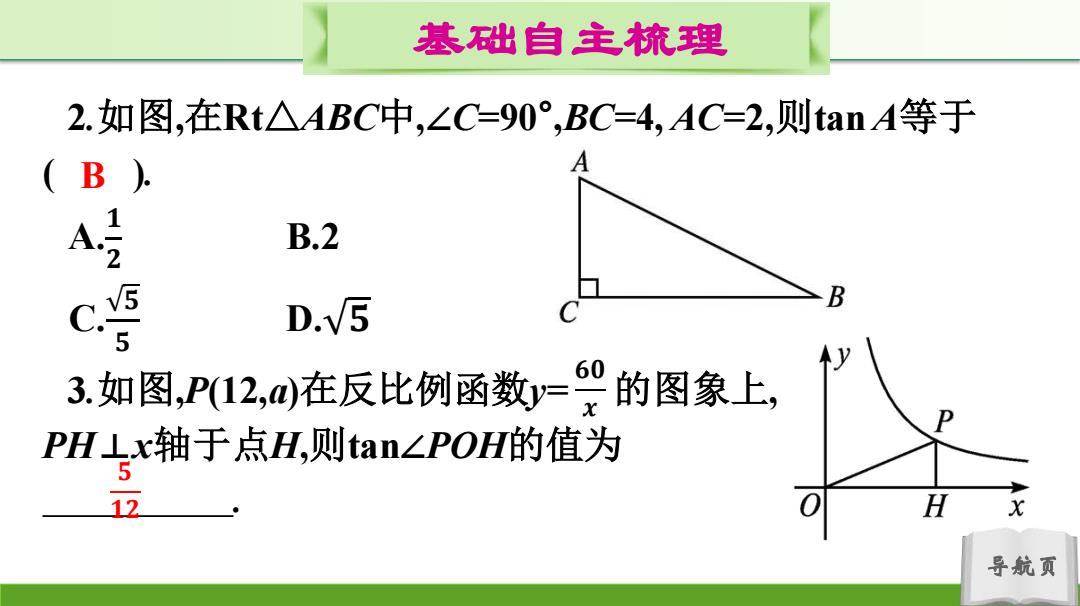
基础自主梳理 2.如图,在Rt△ABC中,∠C=90°,BC=4,AC=2,则tanA等于 B.2 D.V5 5 3如图,P12,在反比例函数=0 的图象上, PHLx轴于点H,则tan∠POH的值为 12 导航页
导航页 基础自主梳理 2.如图,在Rt△ABC中,∠C=90° ,BC=4, AC=2,则tan A等于 ( ). A. 𝟏 𝟐 B.2 C. 𝟓 𝟓 D. 𝟓 3.如图,P(12,a)在反比例函数y= 的图象上, PH⊥x轴于点H,则tan∠POH的值为 . 𝟔𝟎 𝒙 B 𝟓 𝟏𝟐

基础自主梳理 4.坡面的铅直高度与水平宽度的比称为坡度 (或坡比) 导航页
导航页 基础自主梳理 4.坡面的铅直高度与 的比称为坡度 (或 ). 水平宽度 坡比
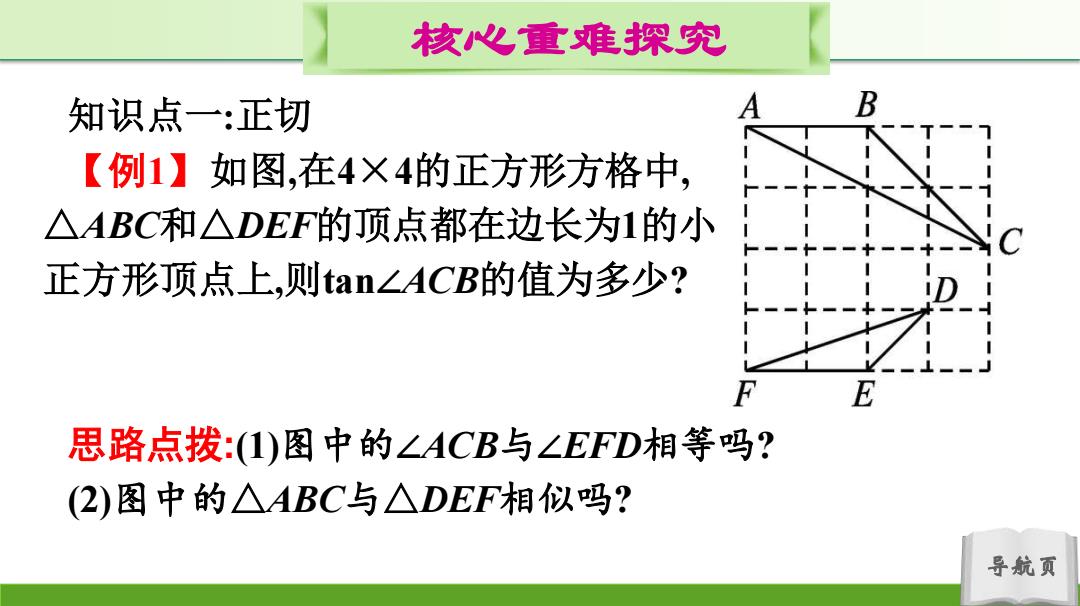
核心重难探究 知识点一:正切 B 【例1】如图,在4×4的正方形方格中, △ABC和△DEF的顶点都在边长为1的小 正方形顶点上,则tan∠ACB的值为多少? F 思路点拨:(1)图中的∠ACB与∠EFD相等吗? (2)图中的△ABC与△DEF相似吗? 导航页
导航页 核心重难探究 知识点一:正切 【例1】如图,在4×4的正方形方格中, △ABC和△DEF的顶点都在边长为1的小 正方形顶点上,则tan∠ACB的值为多少? 思路点拨:(1)图中的∠ACB与∠EFD相等吗? (2)图中的△ABC与△DEF相似吗?

核心重难探究 解:由勾股定理,得BC=2V2,AC=2V√5,DF=V10,DE=V2, ·DF ED FE AC AB BC .'.△FDEC∽△CAB. '.∠DFE=∠ACB ∴tan∠ACB=tan∠DFE号 导航页
导航页 核心重难探究 解:由勾股定理,得 BC=2 𝟐,AC=2 𝟓,DF= 𝟏𝟎,DE= 𝟐, ∴ 𝑫𝑭 𝑨𝑪 = 𝑬𝑫 𝑨𝑩 = 𝑭𝑬 𝑩𝑪 = 𝟐 𝟐 . ∴△FDE∽△CAB. ∴∠DFE=∠ACB. ∴tan ∠ACB=tan ∠DFE=𝟏 𝟑

核心重难探究 【方法归纳】 求一个锐角正切值的方法: (1)若已知两直角边,则直接根据锐角的正切的定义求出正 切值 (2)若已知斜边和一条直角边,则先利用勾股定理求出另一 条直角边,再根据锐角的正切的定义求出正切值, 3)若直接求锐角的正切值有困难,则可利用“相等的角的正 切值相等”转化为求另一个直角三角形的锐角的正切值, 导航页
导航页 核心重难探究 【方法归纳】 求一个锐角正切值的方法: (1)若已知两直角边,则直接根据锐角的正切的定义求出正 切值. (2)若已知斜边和一条直角边,则先利用勾股定理求出另一 条直角边,再根据锐角的正切的定义求出正切值. (3)若直接求锐角的正切值有困难,则可利用“相等的角的正 切值相等”转化为求另一个直角三角形的锐角的正切值
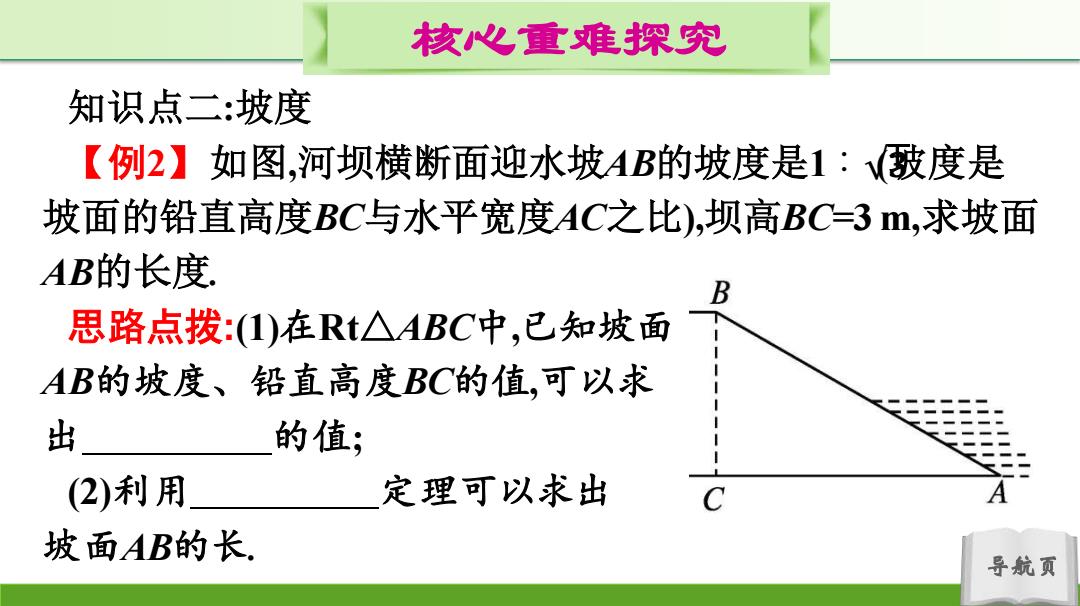
核心重难探究 知识点二:坡度 【例2】如图,河坝横断面迎水坡AB的坡度是1:發度是 坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,求坡面 AB的长度 B 思路点拨:(1)在Rt△ABC中,已知坡面 AB的坡度、铅直高度BC的值,可以求 出 的值; (2)利用 定理可以求出 坡面AB的长. 导航页
导航页 核心重难探究 知识点二:坡度 【例2】如图,河坝横断面迎水坡AB的坡度是1∶ (坡度是 坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 m,求坡面 AB的长度. 思路点拨:(1)在Rt△ABC中,已知坡面 AB的坡度、铅直高度BC的值,可以求 出 的值; (2)利用 定理可以求出 坡面AB的长. 𝟑