
家庭馆亚 4探索三角形相似的条件 第2课时 三角形相似的判定条件(2)
4 探索三角形相似的条件 第2课时 三角形相似的判定条件(2)

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自住梳理 1.相似三角形的判定定理 两边 且夹角 的两个三角形相似 合
基础自主梳理 1.相似三角形的判定定理 两边成比例 且夹角相等 的两个三角形相似

名师指导 1.应用该判定定理证明两个三角形相似时,注意相等的角必 须是已知两对应边的夹角,不要误认为是任意一角对应相等, 这与全等三角形的判定条件“SAS”类似 2.判定两三角形相似,当已知一对角相等时,首先要考虑利用 两角对应相等,两三角形相似的判定方法;然后考虑找夹相等 角的两对对应边的比是否相等.解决此类问题的关键是熟练 掌握相似三角形的判定方法
名师指导 1.应用该判定定理证明两个三角形相似时,注意相等的角必 须是已知两对应边的夹角,不要误认为是任意一角对应相等, 这与全等三角形的判定条件“SAS”类似. 2.判定两三角形相似,当已知一对角相等时,首先要考虑利用 两角对应相等,两三角形相似的判定方法;然后考虑找夹相等 角的两对对应边的比是否相等.解决此类问题的关键是熟练 掌握相似三角形的判定方法

2.能说明△ABC~△A'B'C的条件是(C) AB AC A A'B' A'C AB B. 且∠A=∠C AC A' BC B'C' 且∠B=∠B' D BC ,且∠A=∠A 3.在△ABC与△A'B'C中,∠A=45°,AB=12,AC=15, ∠A'=45°,AB=16,A'C=20,则△ABC与△A'B'C相 (填 “相似”或“不相似”)
2.能说明△ABC∽△A'B'C'的条件是( ). A. 𝑨𝑩 𝑨'𝑩' = 𝑨𝑪 𝑨'𝑪' B. 𝑨𝑩 𝑨𝑪 = 𝑨'𝑩' 𝑨'𝑪' ,且∠A=∠C' C. 𝑨𝑩 𝑨'𝑩' = 𝑩𝑪 𝑩'𝑪' ,且∠B=∠B' D. 𝑨𝑩 𝑨'𝑩' = 𝑩𝑪 𝑨'𝑪' ,且∠A=∠A' 3.在△ABC与△A'B'C'中,∠A=45° ,AB=12,AC=15, ∠A'=45° ,A'B'=16,A'C'=20,则△ABC与△A'B'C'相似 .(填 “相似”或“不相似”) C
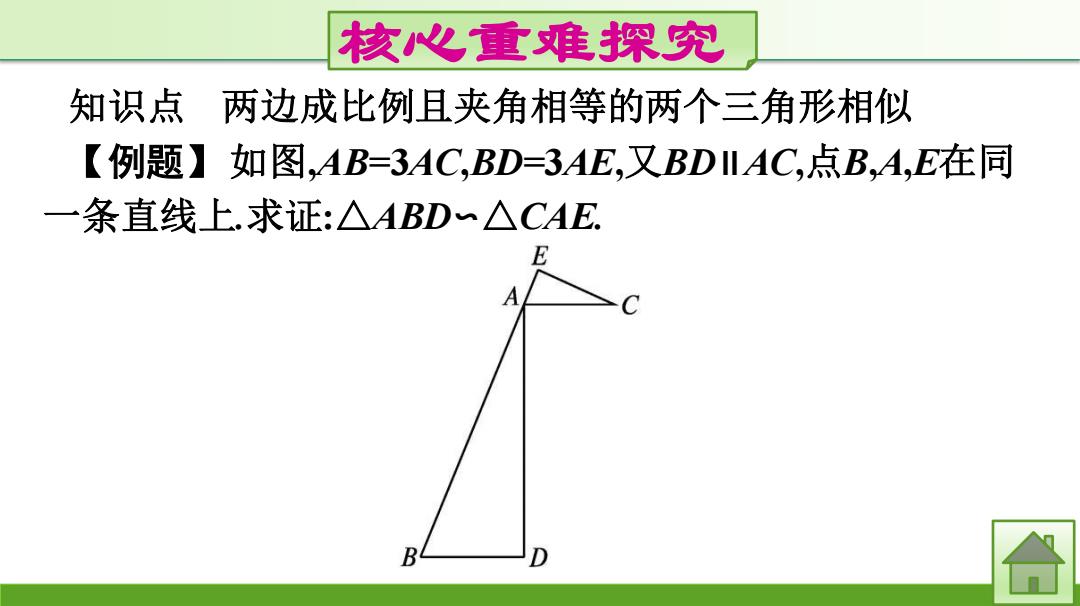
核心重难探究 知识点 两边成比例且夹角相等的两个三角形相似 【例题】如图,AB=3AC,BD=3AE,又BDILAC,点B,A,E在同 一条直线上.求证:△ABD~△CAE. E B D 合
核心重难探究 知识点 两边成比例且夹角相等的两个三角形相似 【例题】如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同 一条直线上.求证:△ABD∽△CAE

思路点拨:1)△ABD与△CAE中有哪组角对应相等?为什么? (2)△ABD与△CAE中有哪组对应边成比例?为什么? 证明:BDIIAC,点B,A,E在同一条直线上, .∴.∠B=∠CAE. .AB=3AC,BD=3AE, ·AB BD =3. ·AC-AE .‘.△ABDSACAE
思路点拨:(1)△ABD与△CAE中有哪组角对应相等?为什么? (2)△ABD与△CAE中有哪组对应边成比例?为什么? 证明:∵BD∥AC,点B,A,E在同一条直线上, ∴∠B=∠CAE. ∵AB=3AC,BD=3AE, ∴ 𝐀𝐁 𝐀𝐂 = 𝐁𝐃 𝐀𝐄 =3. ∴△ABD∽△CAE

【方法归纳】 利用该判定定理判定三角形相似的条件时,要注意以下两点 (1)角:相等的角必是两组对应边的夹角 (2)边:夹角的两边要注意对应,即长边与长边对应、短边与 短边对应
【方法归纳】 利用该判定定理判定三角形相似的条件时,要注意以下两点. (1)角:相等的角必是两组对应边的夹角. (2)边:夹角的两边要注意对应,即长边与长边对应、短边与 短边对应

新知训川练织固 1.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在 图上标注,图(2)中AB,CD交于O点,对于各图中的两个三角形 而言,下列说法正确的是(C), 75° 70° 35° 759 6 8 (1) B A.只有(1)相似 B.只有(2)相似 (2) C.都相似 D.都不相似
新知训练巩固 C 1.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在 图上标注,图(2)中AB,CD交于O点,对于各图中的两个三角形 而言,下列说法正确的是( ). A.只有(1)相似 B.只有(2)相似 C.都相似 D.都不相似 (1) (2)

2.在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,要使 △ABC与△DEF相仪,可以添加条件∠A=∠D(或s=2) (写出一种情况即可) 合
∠A=∠D 或 𝐁𝐂 𝐄𝐅 = 𝟐 2.在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,要使 △ABC与△DEF相似,可以添加条件____________________ (写出一种情况即可)