
家庭缠亚 3 确定二次函数的表达式 第2课时 已知三点确定二次函数表达式(一般式,交点式)
3 确定二次函数的表达式 第2课时 已知三点确定二次函数表达式(一般式,交点式)

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.若给出抛物线上任意三点的坐标,通常可设一般式求表达 式.一般解题思路如下: (1)设二次函数的表达式为y=x2+bx+c(0); (2)把已知的A,B,C三点的坐标代入所设的表达式中,转化为 关于,b,c的三元一次方程组; (3)解方程组求出4,bc的值; (4)把,b,c的值代入所设的表达式中,得出二次函数的 表达式 导航页
导航页 基础自主梳理 1.若给出抛物线上任意三点的坐标,通常可设一般式求表达 式.一般解题思路如下: (1)设二次函数的表达式为 ; (2)把已知的A,B,C三点的坐标代入所设的表达式中,转化为 关于a,b,c的 元一次方程组; (3)解方程组求出 的值; (4)把 的值代入所设的表达式中,得出二次函数的 表达式. y=ax2+bx+c(a≠0) 三 a,b,c a,b,c

基础自主梳理 2.一个二次函数的图象经过(0,0),(-1,-1),(1,9)三点,则这个二 次函数的表达式为y=4x2+5 3.若给出抛物线与x轴的两个交点坐标(c1,0),(化2,0),通常可设 交点式求表达式.一般解题思路如下: (1)设二次函数的表达式为y=a(x-xx-x)(0); (2)把x1x2 的值代入所设的表达式中,转化成关于的 一元一次方程; 导航页
导航页 基础自主梳理 2.一个二次函数的图象经过(0,0),(-1,-1),(1,9)三点,则这个二 次函数的表达式为 . 3.若给出抛物线与x轴的两个交点坐标(x1 ,0),(x2 ,0),通常可设 交点式求表达式.一般解题思路如下: (1)设二次函数的表达式为 ; (2)把 的值代入所设的表达式中,转化成关于a的 一元一次方程; y=4x 2+5x y=a(x-x1 )(x-x2 )(a≠0) x1 ,x2

基础自主梳理 3)解方程求得 a 的值; (4)把 的值代入所设的表达式中,得出二次函数 的表达式 4.经过A(4,0),B(-2,0),C(0,3)三点的抛物线表达式 是厂2++3 导航页
导航页 基础自主梳理 (3)解方程求得 的值; (4)把 的值代入所设的表达式中,得出二次函数 的表达式. 4.经过A(4,0),B(-2,0),C(0,3)三点的抛物线表达式 是 . a a y=- 𝟑 𝟖 x 2 + 𝟑 𝟒 x+3

核心重难探究 知识点一:一般式(已知三点) 【例1】已知二次函数的图象经过点(0,3),(-3,0),(2,-5), (1)试确定此二次函数的表达式; (2)请你判断点P(-2,3)是否在这个二次函数的图象上? 思路点拨:()已知三点的坐标怎样利用待定系数法求出二 次函数表达式? (2)怎样判定所给的点是否在函数的图象上? 导航页
导航页 核心重难探究 知识点一:一般式(已知三点) 【例1】已知二次函数的图象经过点(0,3),(-3,0),(2,-5). (1)试确定此二次函数的表达式; (2)请你判断点P(-2,3)是否在这个二次函数的图象上? 思路点拨:(1)已知三点的坐标怎样利用待定系数法求出二 次函数表达式? (2)怎样判定所给的点是否在函数的图象上?

核心重难探究 解:(1)设此二次函数的表达式为y=x2+bx+c(0), 将(0,3),(-3,0),(2,-5)代入y=x2+bx+c, C=3, (a=-1, 得{9a-3b+3=0,解得{b =-2, 4a+2b+3=-5, c=3. 此二次函数的表达式是y=-x2-2x+3. (2)当x=-2时y=-(-2)2-2X(-2)+3=3,.点P(-2,3)在此二次函数 的图象上 导航页
导航页 核心重难探究 解:(1)设此二次函数的表达式为y=ax2+bx+c(a≠0), 将(0,3),(-3,0),(2,-5)代入y=ax2+bx+c, 得 𝒄 = 𝟑, 𝟗𝒂-𝟑𝒃 + 𝟑 = 𝟎, 𝟒𝒂 + 𝟐𝒃 + 𝟑 = -𝟓, 解得 𝒂 = -𝟏, 𝒃 = -𝟐, 𝒄 = 𝟑. ∴此二次函数的表达式是y=-x 2 -2x+3. (2)当x=-2时,y=-(-2)2 -2×(-2)+3=3,∴点P(-2,3)在此二次函数 的图象上

核心重难探究 【方法归纳】 当知道二次函数图象上三个点的坐标时,通常选用二次函数 的一般式来求函数的关系式 导航页
导航页 核心重难探究 【方法归纳】 当知道二次函数图象上三个点的坐标时,通常选用二次函数 的一般式来求函数的关系式
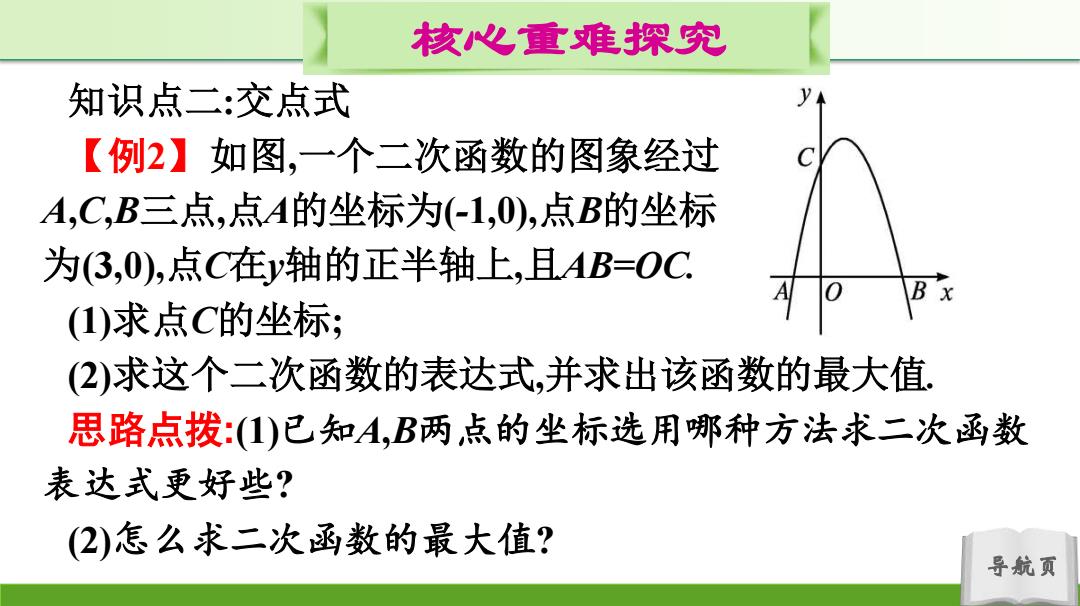
核心心重难探究 知识点二:交点式 【例2】如图,一个二次函数的图象经过 A,C,B三点,点A的坐标为(-1,0),点B的坐标 为(3,0),点C在y轴的正半轴上,且AB=OC ()求点C的坐标; (2)求这个二次函数的表达式,并求出该函数的最大值 思路点拨:(1)已知A,B两点的坐标选用哪种方法求二次函数 表达式更好些? (2)怎么求二次函数的最大值? 导航页
导航页 核心重难探究 知识点二:交点式 【例2】如图,一个二次函数的图象经过 A,C,B三点,点A的坐标为(-1,0),点B的坐标 为(3,0),点C在y轴的正半轴上,且AB=OC. (1)求点C的坐标; (2)求这个二次函数的表达式,并求出该函数的最大值. 思路点拨:(1)已知A,B两点的坐标选用哪种方法求二次函数 表达式更好些? (2)怎么求二次函数的最大值?

核心心重难探究 解:1).A(-1,0),B3,0), .∴AO=1,OB=3,即AB=AO+OB=1+3=4. .0C=4,即点C的坐标为(0,4). (2).A(-1,0),B(3,0), .设二次函数的表达式为y=(c+1)心-3) C0,4),.a0+1)0-3)=4,解得含 4 二次函数的表达式为厂c+1)-3)2+骨+4-等-l+ “一0,当1时y有最大值曾 导航页
导航页 核心重难探究 解:(1)∵A(-1,0),B(3,0), ∴AO=1,OB=3,即AB=AO+OB=1+3=4. ∴OC=4,即点C的坐标为(0,4). (2)∵A(-1,0),B(3,0), ∴设二次函数的表达式为y=a(x+1)(x-3). ∵C(0,4),∴a(0+1)(0-3)=4,解得 a=- 𝟒 𝟑 . ∴二次函数的表达式为 y=- 𝟒 𝟑 (x+1)(x-3)=- 𝟒 𝟑 x 2 + 𝟖 𝟑 x+4=- 𝟒 𝟑 (x-1)2 + 𝟏𝟔 𝟑 . ∵a=- 𝟒 𝟑 <0,∴当 x=1 时,y 有最大值𝟏𝟔 𝟑