
家庭值亚 第1课时 正方形的性质
第1课时 正方形的性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.正方形的定义 有一组邻边 ,并且有一个角是 的平行四边形叫 做正方形 2.正方形的性质定理 (1)正方形的四个角都是 ,四条边 (2)正方形的对角线 且互相 合
基础自主梳理 1.正方形的定义 有一组邻边相等 ,并且有一个角是直角 的平行四边形叫 做正方形. 2.正方形的性质定理 (1)正方形的四个角都是直角 ,四条边相等 . (2)正方形的对角线相等 且互相垂直平分

3.区分平行四边形、矩形、菱形、正方形的性质 (1)从边来看,它们都具有对边平行且相等的性质,而菱形和 正方形还具有四条边相等的性质; (2)从角来看,它们都具有对角相等且邻角互补的性质,而矩 形和正方形还具有四个角都是 的性质; (3)从对角线来看,它们都具有对角线互相平分的性质,而矩 形与正方形的对角线还具有相等的性质,菱形与正方形的对 角线还具有互相垂直的性质!
3.区分平行四边形、矩形、菱形、正方形的性质 (1)从边来看,它们都具有对边平行且相等的性质,而菱形和 正方形还具有四条边相等的性质; (2)从角来看,它们都具有对角相等且邻角互补的性质,而矩 形和正方形还具有四个角都是直角 的性质; (3)从对角线来看,它们都具有对角线互相平分的性质,而矩 形与正方形的对角线还具有相等的性质,菱形与正方形的对 角线还具有互相垂直的性质
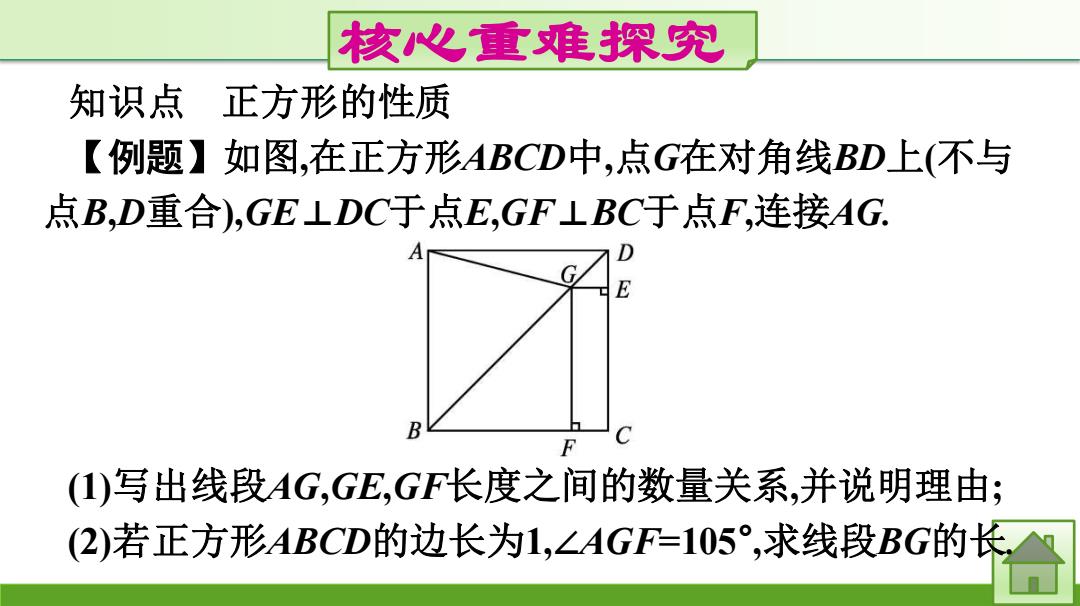
核心重难探究 知识点 正方形的性质 【例题】如图,在正方形ABCD中,点G在对角线BD上(不与 点B,D重合),GE⊥DC于点E,GF LBC于点F,连接AG. B (1)写出线段AG,GE,GF长度之间的数量关系,并说明理由; (2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长
核心重难探究 知识点 正方形的性质 【例题】如图,在正方形ABCD中,点G在对角线BD上(不与 点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG. (1)写出线段AG,GE,GF长度之间的数量关系,并说明理由; (2)若正方形ABCD的边长为1,∠AGF=105° ,求线段BG的长

思路点拨:(1)连接GC,△ADG与△CDG全等吗?由此可得线 段AG与CG具有什么数量关系?在Rt△GEC中,线段CG,GE, EC有什么数量关系? (2)作AH⊥BD于点H,则△ABH与△AGH有何特点?BH,HG 与BG有何数量关系?
思路点拨:(1)连接GC,△ADG与△CDG全等吗?由此可得线 段AG与CG具有什么数量关系?在Rt△GEC中,线段CG,GE, EC有什么数量关系? (2)作AH⊥BD于点H,则△ABH与△AGH有何特点?BH,HG 与BG有何数量关系?
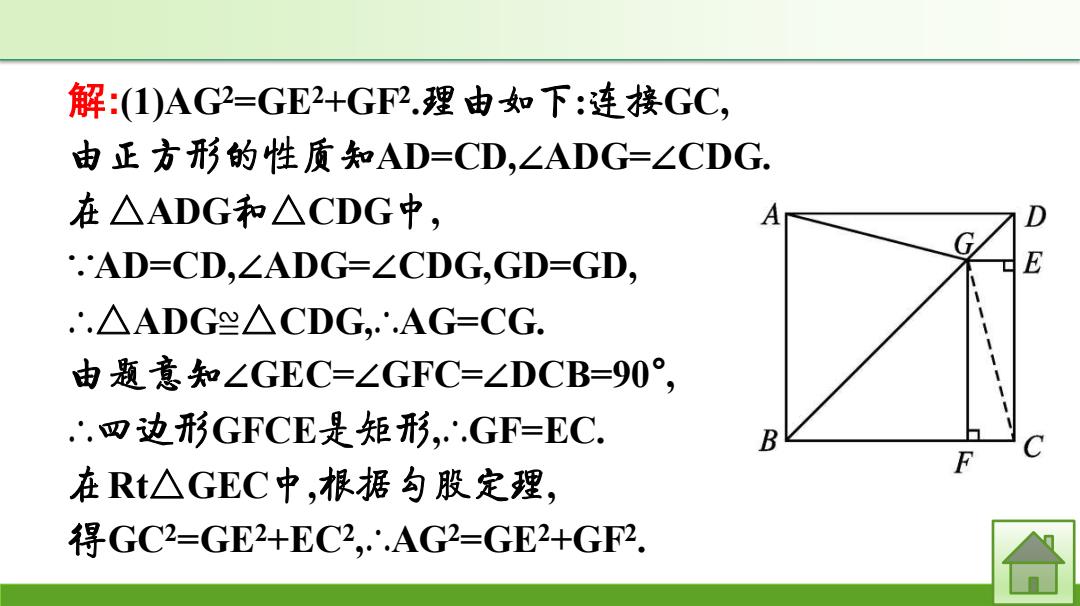
解:1)AG2=GE2+GF2.理由如下:连接GC, 由正方形的性质知AD=CD,∠ADG=∠CDG. 在△ADG和△CDG中, A G .AD=CD,∠ADG=∠CDG,GD=GD, E .△ADG≈△CDG,∴AG=CG. 由题意知∠GEC=∠GFC=∠DCB=0°, .四边形GFCE是矩形,.GF=EC B F 在Rt△GEC中,根据勾股定理, 得GC2=GE2+EC2,∴.AG2=GE2+GF2
解:(1)AG2=GE2+GF2 .理由如下:连接GC, 由正方形的性质知AD=CD,∠ADG=∠CDG. 在△ADG和△CDG中, ∵AD=CD,∠ADG=∠CDG,GD=GD, ∴△ADG≌△CDG,∴AG=CG. 由题意知∠GEC=∠GFC=∠DCB=90° , ∴四边形GFCE是矩形,∴GF=EC. 在Rt△GEC中,根据勾股定理, 得GC2=GE2+EC2 ,∴AG2=GE2+GF2

(2)作AH⊥BD于点H,由题意知∠AGB=60°,∠ABG=45°, ',△ABH为等腰直角三角形,△AGH为含30°角的直角三角 形. G E .AB=1, ∴AH=BH= 2 HG- H BG 6 LV6 21 6 B F C
(2)作AH⊥BD于点H,由题意知∠AGB=60° ,∠ABG=45° , ∴△ABH为等腰直角三角形,△AGH为含30°角的直角三角 形. ∵AB=1, ∴AH=BH= 𝟐 𝟐 ,HG= 𝟔 𝟔 , ∴BG= 𝟐 𝟐 + 𝟔 𝟔
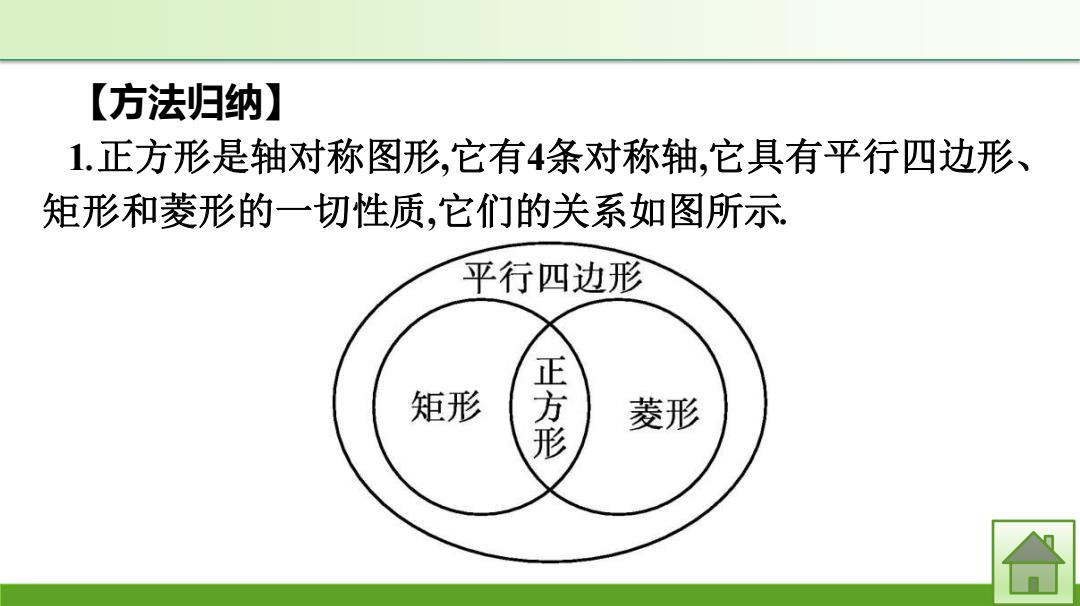
【方法归纳】 1.正方形是轴对称图形,它有4条对称轴,它具有平行四边形、 矩形和菱形的一切性质,它们的关系如图所示 平行四边形 矩形 正方形 菱形 合
【方法归纳】 1.正方形是轴对称图形,它有4条对称轴,它具有平行四边形、 矩形和菱形的一切性质,它们的关系如图所示

2.正方形常与直角三角形、等腰三角形与全等三角形等知 识相联系,综合应用它们解决问题
2.正方形常与直角三角形、等腰三角形与全等三角形等知 识相联系,综合应用它们解决问题