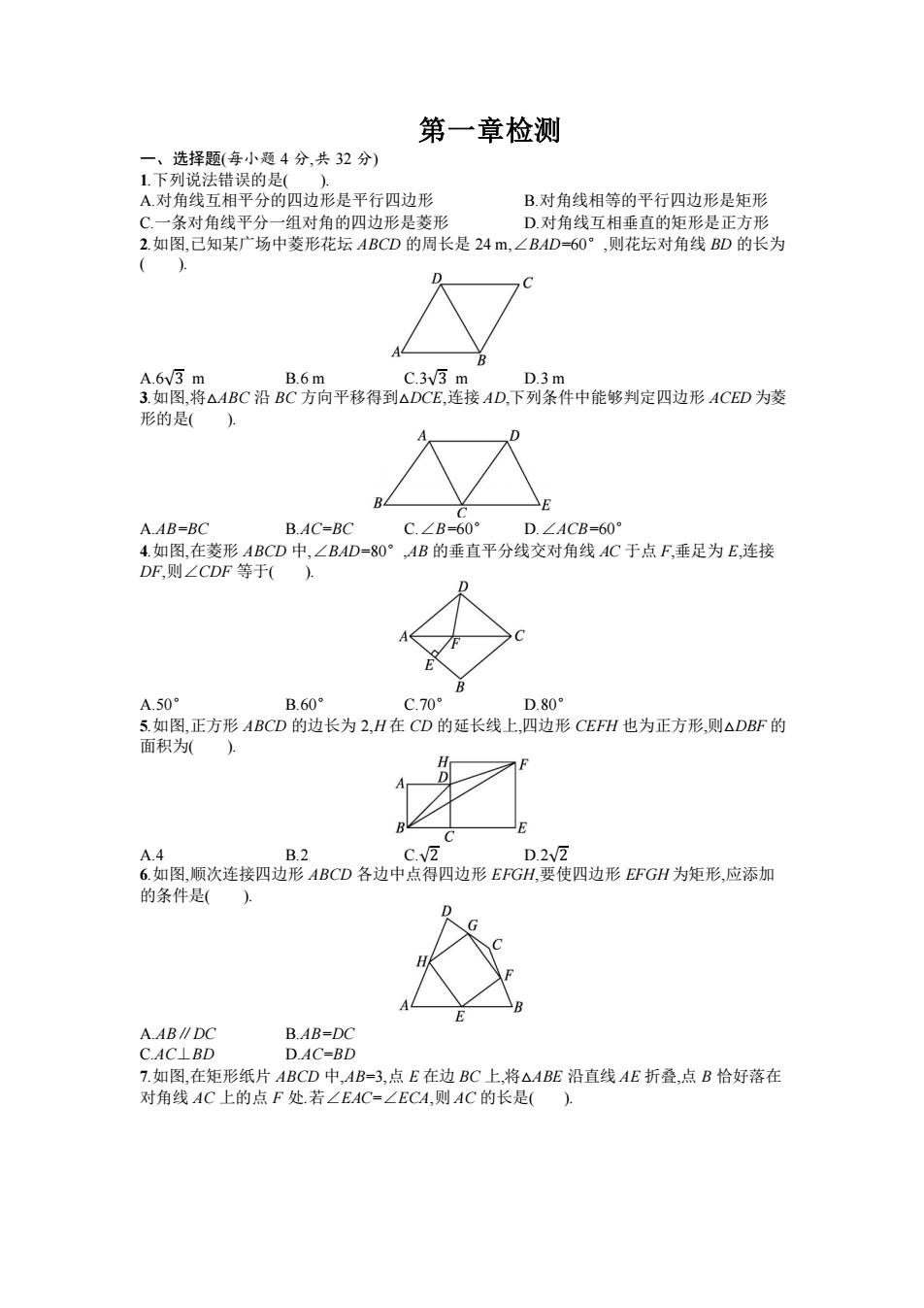
第一章检测 一、选择题(每小题4分,共32分) 1.下列说法错误的是() A对角线互相平分的四边形是平行四边形 B.对角线相等的平行四边形是矩形 C.一条对角线平分一组对角的四边形是菱形 D.对角线互相垂直的矩形是正方形 2.如图,已知某广场中菱形花坛ABCD的周长是24m,∠B4D=60°,则花坛对角线BD的长为 () A.6v3 m B.6m C.3v3 m D.3m 3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱 形的是( B4 A.AB=BC B.AC=BC C.∠B-60° D.∠ACB=60° 4.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接 DF,则∠CDF等于() D A.50° B.60° C.70 D.80 5.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的 面积为(). H A.4 B.2 C.v2 D.2v2 6.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加 的条件是() A.AB∥DC B.AB=DC CAC⊥BD D.AC=BD 7.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在 对角线AC上的点F处.若∠EAC=∠ECA,则AC的长是()
第一章检测 一、选择题(每小题 4 分,共 32 分) 1.下列说法错误的是( ). A.对角线互相平分的四边形是平行四边形 B.对角线相等的平行四边形是矩形 C.一条对角线平分一组对角的四边形是菱形 D.对角线互相垂直的矩形是正方形 2.如图,已知某广场中菱形花坛 ABCD 的周长是 24 m,∠BAD=60°,则花坛对角线 BD 的长为 ( ). A.6√3 m B.6 m C.3√3 m D.3 m 3.如图,将△ABC 沿 BC 方向平移得到△DCE,连接 AD,下列条件中能够判定四边形 ACED 为菱 形的是( ). A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60° 4.如图,在菱形 ABCD 中,∠BAD=80°,AB 的垂直平分线交对角线 AC 于点 F,垂足为 E,连接 DF,则∠CDF 等于( ). A.50° B.60° C.70° D.80° 5.如图,正方形 ABCD 的边长为 2,H 在 CD 的延长线上,四边形 CEFH 也为正方形,则△DBF 的 面积为( ). A.4 B.2 C.√2 D.2√2 6.如图,顺次连接四边形 ABCD 各边中点得四边形 EFGH,要使四边形 EFGH 为矩形,应添加 的条件是( ). A.AB∥DC B.AB=DC C.AC⊥BD D.AC=BD 7.如图,在矩形纸片 ABCD 中,AB=3,点 E 在边 BC 上,将△ABE 沿直线 AE 折叠,点 B 恰好落在 对角线 AC 上的点 F 处.若∠EAC=∠ECA,则 AC 的长是( )
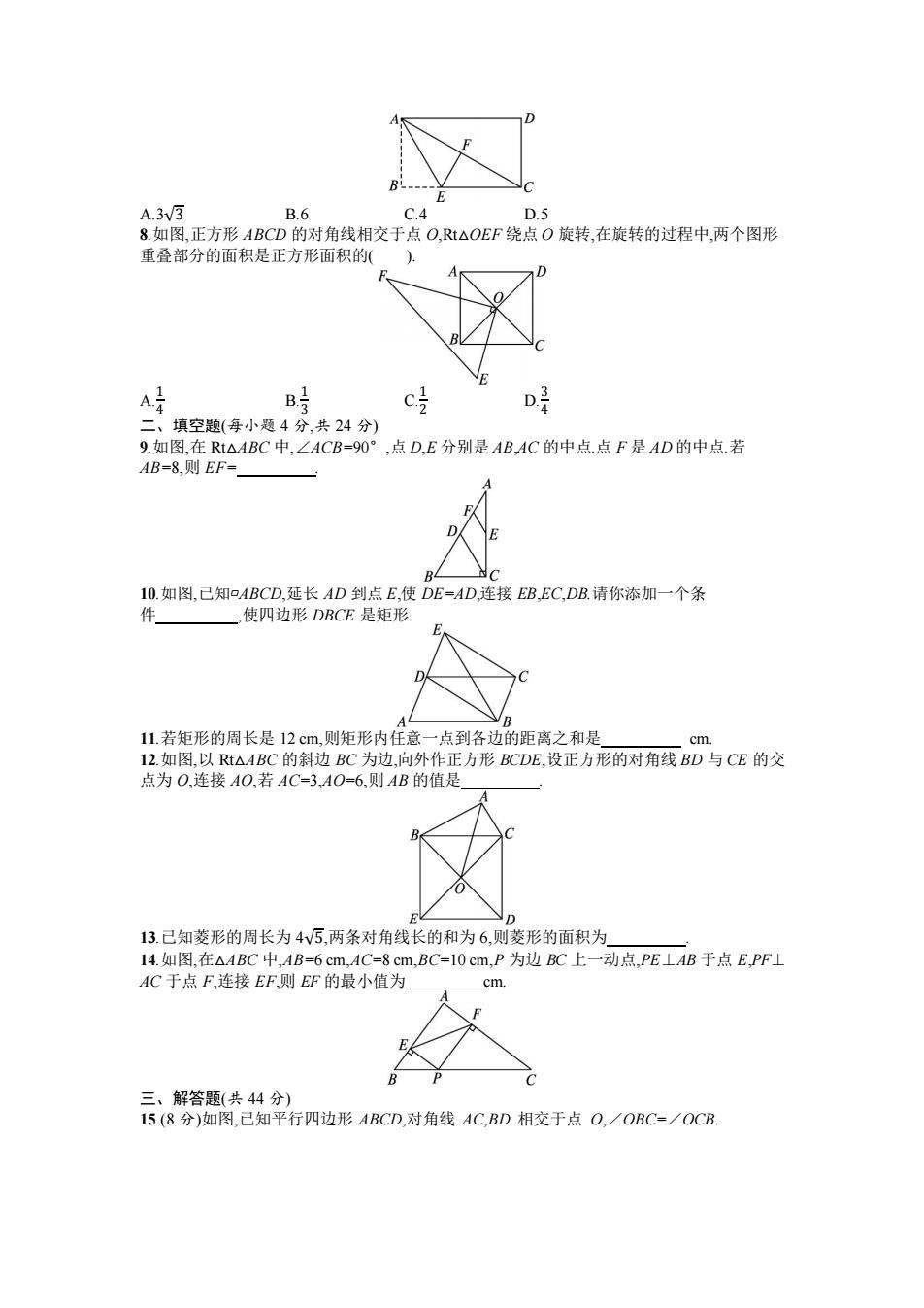
A.3v3 B.6 C.4 D.5 8.如图,正方形ABCD的对角线相交于点O,Rt△OEF绕点O旋转,在旋转的过程中,两个图形 重叠部分的面积是正方形面积的(). A号 B时 C D 二、填空题(每小题4分,共24分) 9.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点.点F是AD的中点.若 AB=8,则EF= I0.如图,己知PABCD,延长AD到点E,使DE=AD,连接EB,EC,DB.请你添加一个条 件 ,使四边形DBCE是矩形. 11.若矩形的周长是12cm,则矩形内任意一点到各边的距离之和是 cm. 12.如图,以Rt△ABC的斜边BC为边,向外作正方形BCDE,设正方形的对角线BD与CE的交 点为O,连接AO,若AC=3,AO=6,则AB的值是 E D 13.己知菱形的周长为4√5,两条对角线长的和为6,则菱形的面积为 14.如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于点E,PF⊥ AC于点F,连接EF,则EF的最小值为 cm. 三、解答题(共44分) 15.(8分)如图,己知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB
A.3√3 B.6 C.4 D.5 8.如图,正方形 ABCD 的对角线相交于点 O,Rt△OEF 绕点 O 旋转,在旋转的过程中,两个图形 重叠部分的面积是正方形面积的( ). A. 1 4 B. 1 3 C. 1 2 D. 3 4 二、填空题(每小题 4 分,共 24 分) 9.如图,在 Rt△ABC 中,∠ACB=90°,点 D,E 分别是 AB,AC 的中点.点 F 是 AD 的中点.若 AB=8,则 EF= . 10.如图,已知▱ABCD,延长 AD 到点 E,使 DE=AD,连接 EB,EC,DB.请你添加一个条 件 ,使四边形 DBCE 是矩形. 11.若矩形的周长是 12 cm,则矩形内任意一点到各边的距离之和是 cm. 12.如图,以 Rt△ABC 的斜边 BC 为边,向外作正方形 BCDE,设正方形的对角线 BD 与 CE 的交 点为 O,连接 AO,若 AC=3,AO=6,则 AB 的值是 . 13.已知菱形的周长为 4√5,两条对角线长的和为 6,则菱形的面积为 . 14.如图,在△ABC 中,AB=6 cm,AC=8 cm,BC=10 cm,P 为边 BC 上一动点,PE⊥AB 于点 E,PF⊥ AC 于点 F,连接 EF,则 EF 的最小值为 cm. 三、解答题(共 44 分) 15.(8 分)如图,已知平行四边形 ABCD,对角线 AC,BD 相交于点 O,∠OBC=∠OCB

(1)求证:平行四边形ABCD是矩形: (2)请添加一个条件使矩形ABCD为正方形 16.(8分)如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠ BEF,∠DFE的平分线交于点H易证∠EHF=∠EGF-∠GEH-90°,从而可知四边形EGFH 是矩形 E 小明继续进行了探索,过点G作MN∥EF,分别交AB,CD于点M,N,过点H作PQ∥EF,分别交 AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全 他的证明思路,并写出证明过程. 由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证平行四边形MNQP是 菱形,只要证MN=NQ.由己知条件 MN∥EF,故只要证GM=FQ,即证 △MGE≌△QFH.易证 故只要证∠MGE=∠QFH 易证∠MGE=∠GEF,∠QFH=∠EFH, 即可得证. 17.(8分)如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于 点MN. 0 (1)求证:四边形BNDM是菱形; (2)若BD=24,MW=10,求菱形BNDM的周长
(1)求证:平行四边形 ABCD 是矩形; (2)请添加一个条件使矩形 ABCD 为正方形. 16.(8 分)如图,AB∥CD,点 E,F 分别在 AB,CD 上,连接 EF,∠AEF,∠CFE 的平分线交于点 G,∠ BEF,∠DFE 的平分线交于点 H.易证∠EHF=∠EGF=∠GEH=90°,从而可知四边形 EGFH 是矩形. 小明继续进行了探索,过点 G 作 MN∥EF,分别交 AB,CD 于点 M,N,过点 H 作 PQ∥EF,分别交 AB,CD 于点 P,Q,得到四边形 MNQP,此时,他猜想四边形 MNQP 是菱形,请在下列框中补全 他的证明思路,并写出证明过程. 由 AB∥CD,MN∥EF,PQ∥EF,易证四边形 MNQP 是平行四边形.要证平行四边形 MNQP 是 菱形,只要证 MN=NQ.由已知条件 ,MN∥EF,故只要证 GM=FQ,即证 △MGE≌△QFH.易证 , ,故只要证∠MGE=∠QFH. 易证∠MGE=∠GEF,∠QFH=∠EFH, ,即可得证. 17.(8 分)如图,在四边形 ABCD 中,AD∥BC,对角线 BD 的垂直平分线与边 AD,BC 分别相交于 点 M,N. (1)求证:四边形 BNDM 是菱形; (2)若 BD=24,MN=10,求菱形 BNDM 的周长
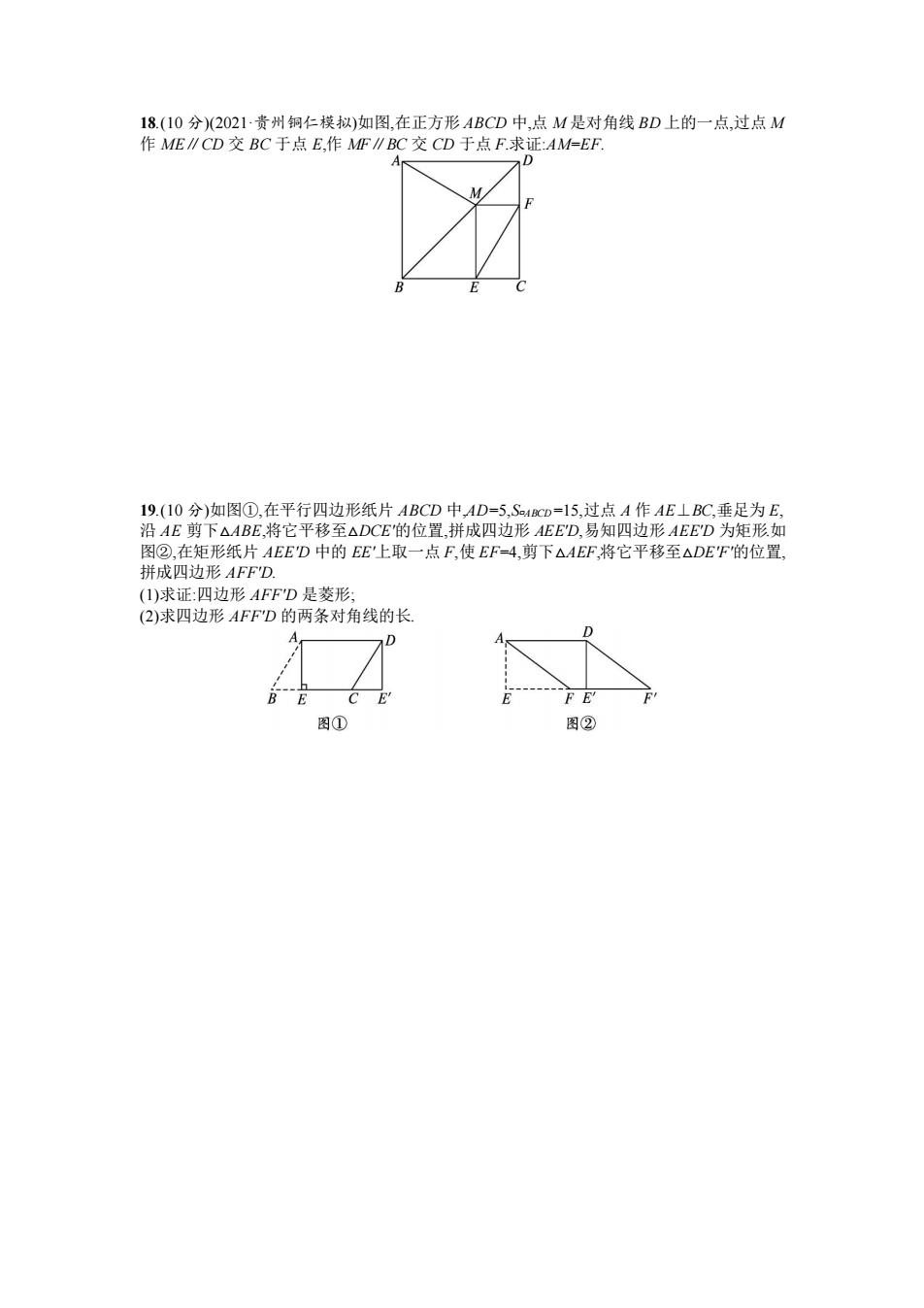
18.(10分)(2021贵州铜仁模拟)如图,在正方形ABCD中,点M是对角线BD上的一点,过点M 作ME∥CD交BC于点E,作MF∥BC交CD于点F求证:AM=EF. 4 M 19.(10分)如图①,在平行四边形纸片ABCD中,AD=5,S4CD=15,过点A作AE⊥BC,垂足为E, 沿AE剪下△ABE,将它平移至△DCE的位置,拼成四边形AEE'D,易知四边形AEE'D为矩形如 图②,在矩形纸片AEE'D中的EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DEF的位置, 拼成四边形AFF'D. (1)求证:四边形AFFD是菱形: (2)求四边形AFF'D的两条对角线的长 BE F E 图① 图②
18.(10 分)(2021·贵州铜仁模拟)如图,在正方形 ABCD 中,点 M 是对角线 BD 上的一点,过点 M 作 ME∥CD 交 BC 于点 E,作 MF∥BC 交 CD 于点 F.求证:AM=EF. 19.(10 分)如图①,在平行四边形纸片 ABCD 中,AD=5,S▱ABCD=15,过点 A 作 AE⊥BC,垂足为 E, 沿 AE 剪下△ABE,将它平移至△DCE'的位置,拼成四边形 AEE'D,易知四边形 AEE'D 为矩形.如 图②,在矩形纸片 AEE'D 中的 EE'上取一点 F,使 EF=4,剪下△AEF,将它平移至△DE'F'的位置, 拼成四边形 AFF'D. (1)求证:四边形 AFF'D 是菱形; (2)求四边形 AFF'D 的两条对角线的长

第一章检测 一、选择题 1.C2.B3.B4.B5.B6.C7.B8.A 二、填空题 9.210.∠EDB=90°(答案不唯一) 161262313.414号 三、解答题 15.(1)证明:四边形ABCD是平行四边形, ..OA=OC,OB=OD. :∠OBC=∠OCB,:OB=OC,AC=BD .:平行四边形ABCD是矩形. (2)解AB=AD(或AC⊥BD)(答案不唯一). 16.解FG平分∠CFE GE=FH∠GME=∠FQH∠GEF=∠EFH 证明过程如下: :MN∥EF,PQ∥EF,.:MN∥PQ. 又MP∥NQ,:四边形MWOP是平行四边形 由题意知四边形GFHE为矩形,:GE=FH. :'∠MGE=∠GEF=∠EFH=∠QFH,∠GME=∠FQH,.:△MGE≌△QFH.:MG=FQ :'∠NGF=∠GFE=∠NFG,.:NG=NF .MN=NG+GM=NF+FO=NO. .:平行四边形MNOP是菱形. 17.(1)证明AD∥BC,.:∠DMO=∠BNO. :MN是对角线BD的垂直平分线,.:OB=OD,MN⊥BD 在△MOD和△NOB中,∠DMO=∠BNO,∠MOD=∠NOB,OD-OB, .:△MOD≌△NOB(AAS),.:OM=ON. :OB=OD,:四边形BNDM是平行四边形 :MN⊥BD,:四边形BNDM是菱形. (2)解:四边形BNDM是菱形,BD=24,MN=10, .:BM=BN=DM-=DN.0B--BD=12.0M--MN-5. 在Rt△BOM中,由勾股定理得BM=√OM2+OB=V52+12Z-13, .:菱形BNDM的周长=4BM=4×13=52 18.证明延长EM交AD于点P,延长FM交AB于点Q,如图所示 A :'四边形ABCD为正方形,点M为对角线BD上一点,:∠MDF=∠MDP=∠MBE=∠ MBQ=45°, ..DF=MF=DP=MP,BE=ME=BO=MO .:四边形PMFD,BEMQ为正方形 :AP∥QM,AQ∥PM,∠PAQ=90°,CF∥EM,MF∥EC,∠ECF=90°, .:四边形AQMP,MECF为矩形, .:.AO=PM=FM
第一章检测 一、选择题 1.C 2.B 3.B 4.B 5.B 6.C 7.B 8.A 二、填空题 9.2 10.∠EDB=90°(答案不唯一) 11.6 12.6√2-3 13.4 14. 24 5 三、解答题 15.(1)证明 ∵四边形 ABCD 是平行四边形, ∴OA=OC,OB=OD. ∵∠OBC=∠OCB,∴OB=OC,∴AC=BD, ∴平行四边形 ABCD 是矩形. (2)解 AB=AD(或 AC⊥BD)(答案不唯一). 16.解 FG 平分∠CFE GE=FH ∠GME=∠FQH ∠GEF=∠EFH 证明过程如下: ∵MN∥EF,PQ∥EF,∴MN∥PQ. 又 MP∥NQ,∴四边形 MNQP 是平行四边形. 由题意知四边形 GFHE 为矩形,∴GE=FH. ∵∠MGE=∠GEF=∠EFH=∠QFH,∠GME=∠FQH,∴△MGE≌△QFH.∴MG=FQ. ∵∠NGF=∠GFE=∠NFG,∴NG=NF. ∴MN=NG+GM=NF+FQ=NQ, ∴平行四边形 MNQP 是菱形. 17.(1)证明 ∵AD∥BC,∴∠DMO=∠BNO. ∵MN 是对角线 BD 的垂直平分线,∴OB=OD,MN⊥BD. 在△MOD 和△NOB 中,∠DMO=∠BNO,∠MOD=∠NOB,OD=OB, ∴△MOD≌△NOB(AAS),∴OM=ON. ∵OB=OD,∴四边形 BNDM 是平行四边形. ∵MN⊥BD,∴四边形 BNDM 是菱形. (2)解 ∵四边形 BNDM 是菱形,BD=24,MN=10, ∴BM=BN=DM=DN,OB=1 2 BD=12,OM=1 2 MN=5. 在 Rt△BOM 中,由勾股定理得 BM=√𝑂𝑀2 + 𝑂𝐵 2 = √5 2 + 12 2=13, ∴菱形 BNDM 的周长=4BM=4×13=52. 18.证明 延长 EM 交 AD 于点 P,延长 FM 交 AB 于点 Q,如图所示. ∵四边形 ABCD 为正方形,点 M 为对角线 BD 上一点,∴∠MDF=∠MDP=∠MBE=∠ MBQ=45°, ∴DF=MF=DP=MP,BE=ME=BQ=MQ, ∴四边形 PMFD,BEMQ 为正方形. ∵AP∥QM,AQ∥PM,∠PAQ=90°,CF∥EM,MF∥EC,∠ECF=90°, ∴四边形 AQMP,MECF 为矩形, ∴AQ=PM=FM

(AQ FM, 在△AQM和△FME中LAQM=LFME=90°, OM=ME. .:△AQM≌△FME(SAS),.:AM=EF 19.(1)证明:AD=5,SAcD=15,AE=3. :EF=4..:AF=VAE2+EF2=V32+42=5. .·AF=AD=5. :AF∥DF,AF=DF,:四边形AFFD是菱形 (2)解连接AF,DF,如图. 在Rt△DEF中, :E'F=E'E-EF=5-4=1,DE=3, .:DF=V12+3=V10 由S-ARCD=-15,得S#AFFD=15,故有;×V1而AF=15,解得AF-=3V而
在△AQM 和△FME 中,{ 𝐴𝑄 = 𝐹𝑀, ∠𝐴𝑄𝑀 = ∠𝐹𝑀𝐸 = 90°, 𝑄𝑀 = 𝑀𝐸, ∴△AQM≌△FME(SAS),∴AM=EF. 19.(1)证明 ∵AD=5,S▱ABCD=15,∴AE=3. ∵EF=4,∴AF=√𝐴𝐸 2 + 𝐸𝐹 2 = √3 2 + 4 2=5. ∴AF=AD=5. ∵AF∥DF',AF=DF',∴四边形 AFF'D 是菱形. (2)解 连接 AF',DF,如图. 在 Rt△DE'F 中, ∵E'F=E'E-EF=5-4=1,DE'=3, ∴DF=√1 2 + 3 2 = √10. 由 S▱ABCD=15,得 S 菱形 AFF'D=15,故有1 2 × √10·AF'=15,解得 AF'=3√10