
第三章检测 一、选择题(每小题4分,共32分) 1.在一个不透明的盒子中装有α个除颜色外完全相同的球,这a个球中只有2个红球若每次 将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红 球的频率稳定在10%左右,则a的值大约为( A.10 B.20 C.18 D.25 2.某班九年级一共有1,2,3,4四个班,从这四个班中随机抽取两个班进行一场篮球比赛,则恰好 抽到1班和2班的概率是( A后 B c啞 D哈 3.如图,一只蚂蚁在树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食 物的概率是(). r物 蚂蚁 B 4.有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙能打开另一把锁.任 意取出一把钥匙去开任意的一把锁,一次能打开锁的概率是( ) A分 B c味 D 5.三名初三学生坐在仅有的三个座位上,起身后重新就座,恰好有两名同学没有坐回原位的概 率是( A号 B陪 c味 D吃 6.投掷一枚质地均匀的骰子两次,向上一面的点数依次记为a,b,则关于x的方程x2+ar+b=0 有解的概率是( A号 B时 15 D岩 7.学生甲与学生乙玩一种转盘游戏两个完全相同的转盘如图所示,每个转盘被分成面积相等 的四个区域,分别用数字“1*2*3*4”表示固定指针,同时转动两个转盘,任其自由停止,若两 指针所指数字的积为奇数,则甲获胜:若两指针所指数字的积为偶数,则乙获胜:若指针指向扇 形的分界线,则都重转一次在该游戏中乙获胜的概率是( A B时 C D.3 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次 抽奖的机会,将图中的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字抽奖规则如下: 抽奖者连续转动转盘两次转盘停止后指针所指扇形内的数字为每次所得的数(若指针指在分 界线时重转),当两次所得的数字之和为8时,返现金20元,当两次所得数字之和为7时,返现 金15元,当两次所得数字之和为6时,返现金10元:当两次所得数字之和为其他数时,不返现 金某顾客参加一次抽奖,获得返还现金的概率是(
第三章检测 一、选择题(每小题 4 分,共 32 分) 1.在一个不透明的盒子中装有 a 个除颜色外完全相同的球,这 a 个球中只有 2 个红球.若每次 将球充分搅匀后,任意摸出 1 个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红 球的频率稳定在 10%左右,则 a 的值大约为( ). A.10 B.20 C.18 D.25 2.某班九年级一共有 1,2,3,4 四个班,从这四个班中随机抽取两个班进行一场篮球比赛,则恰好 抽到 1 班和 2 班的概率是( ). A. 1 8 B. 3 8 C. 1 2 D. 1 6 3.如图,一只蚂蚁在树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食 物的概率是( ). A. 1 6 B. 1 4 C. 1 3 D. 1 2 4.有两把不同的锁和三把钥匙,其中两把钥匙能打开同一把锁,第三把钥匙能打开另一把锁.任 意取出一把钥匙去开任意的一把锁,一次能打开锁的概率是( ). A. 1 2 B. 1 3 C. 1 4 D. 2 3 5.三名初三学生坐在仅有的三个座位上,起身后重新就座,恰好有两名同学没有坐回原位的概 率是( ). A. 1 9 B. 1 6 C. 1 4 D. 1 2 6.投掷一枚质地均匀的骰子两次,向上一面的点数依次记为 a,b,则关于 x 的方程 x 2+ax+b=0 有解的概率是( ). A. 1 2 B. 1 3 C. 8 15 D. 19 36 7.学生甲与学生乙玩一种转盘游戏.两个完全相同的转盘如图所示,每个转盘被分成面积相等 的四个区域,分别用数字“1”“2”“3”“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两 指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇 形的分界线,则都重转一次.在该游戏中乙获胜的概率是( ). A. 1 4 B. 1 2 C. 3 4 D. 5 6 8.某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次 抽奖的机会,将图中的圆形转盘平均分成四个扇形,分别标上 1,2,3,4 四个数字.抽奖规则如下: 抽奖者连续转动转盘两次,转盘停止后指针所指扇形内的数字为每次所得的数(若指针指在分 界线时重转),当两次所得的数字之和为 8 时,返现金 20 元;当两次所得数字之和为 7 时,返现 金 15 元;当两次所得数字之和为 6 时,返现金 10 元;当两次所得数字之和为其他数时,不返现 金.某顾客参加一次抽奖,获得返还现金的概率是( )

A B品 c始 D唱 、填空题(每小题4分,共24分) 9.已知事件A发生的概率为分大量重复做这种试验,事件A平均每100次发生的次数 10.一个不透明的盒子里放置三张除所标数字外其他完全相同的卡片,分别标有数字1,2,3.随 机抽取1张,放回后再随机抽取1张,则抽得的第二张卡片上的数字大于第一张卡片上的数字 的概率为 11.在一个不透明的盒子中装有α个除颜色外完全相同的球.其中只有6个白球.每次将球充 分搅匀,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验,发现摸到白球的频率稳 定在20%左右,则a的值约为 12.小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球3000个,这些塑料球除颜色 外,其余均相同.为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出 一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近 波动,据此可以估计黑球的个数是 13.一个能自由转动的正六边形转盘如图所示,这个转盘被三条分割线分成形状相同、面积相 等的三部分,且分别标有1,2,3三个数字,指针的位置固定不动,让转盘自由转动2次,每次转盘 停止后,记录指针指向的数(当指针指向分割线时重转),则2次指向的数都是奇数的概率 为 14.(2021贵州钢仁模拟)现有两组扑克牌,每组三张扑克,第一组分别是红桃5、红桃6、红桃 7,第二组分别是梅花3、梅花4、梅花5,若把两组扑克牌背面朝上各自搅匀,并分别从两组中 各抽取一张牌,试求“抽出两张牌的数字之和为10”的概率是」 三、解答题(共44分) 15.(9分)锐锐参加某市电视台组织的智力竞答节目,答对最后两道单选题就顺利通关第一道 单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求 助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项), (1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 (2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 (3)如果锐锐在每道题各用一次“求助”,请用树状图或者列表来分析他通关的概率 16.(7分)某校准备组建“校园安全宣传队”,每班有两个队员名额,七年级(2)班有甲、乙、丙、 丁四名同学报名,这四名同学综合素质都很好王老师决定采取抽签的方式确定人选.具体做 法是将甲、乙、丙、丁四名同学分别编号为1,2,3,4号,将号码分别写在4个大小、质地、 颜色均无差别的小球上,然后把小球放入不透明的袋子中,充分搅拌均匀后,王老师从袋中随 机摸出2个小球,根据小球上的编号确定本班“校园安全宣传队”人选, (1)用画树状图法,写出“王老师从袋中随机摸出2个小球”可能出现的所有结果; (2)求甲同学被选中的概率
A. 3 8 B. 5 16 C. 1 8 D. 5 8 二、填空题(每小题 4 分,共 24 分) 9.已知事件 A 发生的概率为 1 20,大量重复做这种试验,事件 A 平均每 100 次发生的次数 是 . 10.一个不透明的盒子里放置三张除所标数字外其他完全相同的卡片,分别标有数字 1,2,3.随 机抽取 1 张,放回后再随机抽取 1 张,则抽得的第二张卡片上的数字大于第一张卡片上的数字 的概率为 . 11.在一个不透明的盒子中装有 a 个除颜色外完全相同的球,其中只有 6 个白球.每次将球充 分搅匀,任意摸出 1 个球记下颜色后再放回盒子,通过大量重复试验,发现摸到白球的频率稳 定在 20%左右,则 a 的值约为 . 12.小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球 3 000 个,这些塑料球除颜色 外,其余均相同.为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出 一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在 0.7 附近 波动,据此可以估计黑球的个数是 . 13.一个能自由转动的正六边形转盘如图所示,这个转盘被三条分割线分成形状相同、面积相 等的三部分,且分别标有 1,2,3 三个数字,指针的位置固定不动,让转盘自由转动 2 次,每次转盘 停止后,记录指针指向的数(当指针指向分割线时重转),则 2 次指向的数都是奇数的概率 为 . 14.(2021·贵州铜仁模拟)现有两组扑克牌,每组三张扑克,第一组分别是红桃 5、红桃 6、红桃 7,第二组分别是梅花 3、梅花 4、梅花 5,若把两组扑克牌背面朝上各自搅匀,并分别从两组中 各抽取一张牌,试求“抽出两张牌的数字之和为 10”的概率是 . 三、解答题(共 44 分) 15.(9 分)锐锐参加某市电视台组织的智力竞答节目,答对最后两道单选题就顺利通关.第一道 单选题有 3 个选项,第二道单选题有 4 个选项,这两道题锐锐都不会,不过锐锐还有两个“求 助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项). (1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 . (2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 . (3)如果锐锐在每道题各用一次“求助”,请用树状图或者列表来分析他通关的概率. 16.(7 分)某校准备组建“校园安全宣传队”,每班有两个队员名额,七年级(2)班有甲、乙、丙、 丁四名同学报名,这四名同学综合素质都很好,王老师决定采取抽签的方式确定人选.具体做 法是:将甲、乙、丙、丁四名同学分别编号为 1,2,3,4 号,将号码分别写在 4 个大小、质地、 颜色均无差别的小球上,然后把小球放入不透明的袋子中,充分搅拌均匀后,王老师从袋中随 机摸出 2 个小球,根据小球上的编号确定本班“校园安全宣传队”人选. (1)用画树状图法,写出“王老师从袋中随机摸出 2 个小球”可能出现的所有结果; (2)求甲同学被选中的概率

17.(8分)甲、乙两队进行乒乓球团体赛比赛规则:两队之间进行3局比赛3局比赛必须全部 打完,赢2局的队为获胜队.假如甲、乙两队之间每局比赛输赢的机会相同,且甲队己经赢得 了第1局比赛,那么甲队最终获胜的概率是多少? 18.(8分)若n是一个两位正整数,且n的个位数字大于十位数字,则称n为两位递增数”(如 13,35,56等).现从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数 (1)写出所有个位数字是5的“两位递增数”, (2)求抽取的两位递增数”的个位数字与十位数字之积能被10整除的概率 19.(12分)在一次数学兴趣小组活动中,李燕和刘凯两名同学设计了两个转盘做游戏(每个转 盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字)如图所示游戏规则如下: 两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数之和小于12,则李燕获胜: 若指针所指区域内两数之和等于12,则为平局;若指针所指区域内两数之和大于12,则刘凯获 胜:若指针停在等分线上,重转一次,直到指针指向某一份内为止 (1)请用列表或画树状图的方法表示出上述游戏中两数之和的所有可能的结果 (2)分别求出李燕和刘凯获胜的概率
17.(8 分)甲、乙两队进行乒乓球团体赛.比赛规则:两队之间进行 3 局比赛,3 局比赛必须全部 打完,赢 2 局的队为获胜队.假如甲、乙两队之间每局比赛输赢的机会相同,且甲队已经赢得 了第 1 局比赛,那么甲队最终获胜的概率是多少? 18.(8 分)若 n 是一个两位正整数,且 n 的个位数字大于十位数字,则称 n 为“两位递增数”(如 13,35,56 等).现从由数字 1,2,3,4,5,6 构成的所有的“两位递增数”中随机抽取 1 个数. (1)写出所有个位数字是 5 的“两位递增数”; (2)求抽取的“两位递增数”的个位数字与十位数字之积能被 10 整除的概率. 19.(12 分)在一次数学兴趣小组活动中,李燕和刘凯两名同学设计了两个转盘做游戏(每个转 盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字)如图所示.游戏规则如下: 两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数之和小于 12,则李燕获胜; 若指针所指区域内两数之和等于 12,则为平局;若指针所指区域内两数之和大于 12,则刘凯获 胜;若指针停在等分线上,重转一次,直到指针指向某一份内为止. (1)请用列表或画树状图的方法表示出上述游戏中两数之和的所有可能的结果; (2)分别求出李燕和刘凯获胜的概率
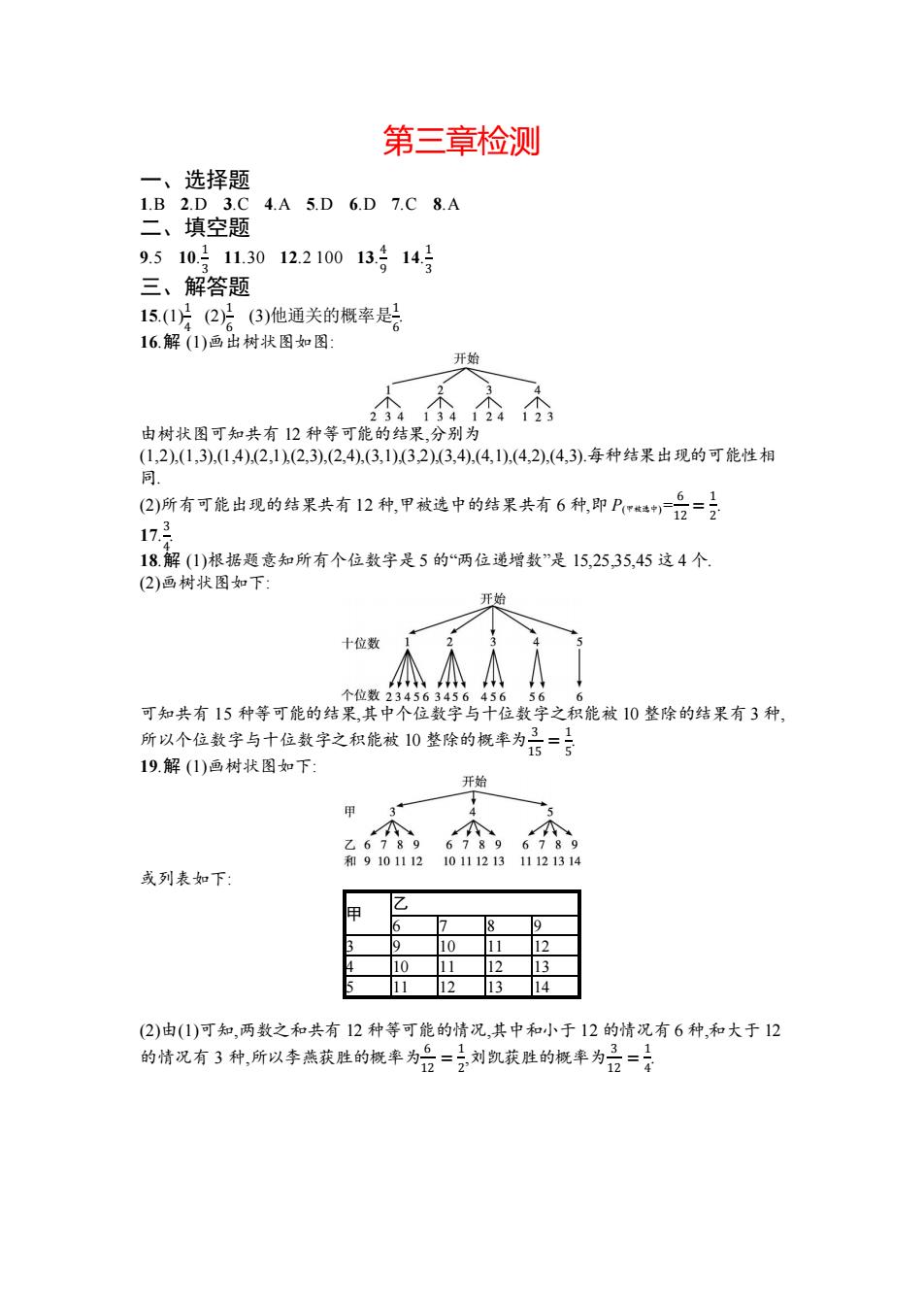
第三章检测 一、选择题 1.B2.D3.C4.A5.D6.D7.C8.A 二、填空题 9.510.311.3012.210013号143 三、解答题 15.(1片2片(6)他通关的概率是号 16.解(1)画出树状图如图: 开始 由树状图可知共有12种等可能的结果,分别为 (1,2),(1,3),(14),.(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3).每种结果出现的可能性相 同 (2)所有可能出现的结果共有12种,甲被选中的结果共有6种,即P~4)豆= 61 17 8.解(1)根据题意知所有个位数字是5的“两位递增数”是15,25,35,45这4个 (2)画树状图如下: 开始 十位数 个位数234563456456 56 可知共有15种等可能的结果,其中个位数字与十位数字之积能被10整除的结果有3种, 所以个位数字与十位数字之积能被10整除的概率为品=专 19.解(1)画树状图如下: 开始 甲 乙6789 67896789 和91011121011121311121314 或列表如下: 9 10 12 10 13 11 13 14 (2)由(1)可知,两数之和共有12种等可能的情况,其中和小于12的情况有6种,和大于12 的情况有3种,所以李燕获胜的概率为始=之刘凯获胜的概率为品-号 12
第三章检测 一、选择题 1.B 2.D 3.C 4.A 5.D 6.D 7.C 8.A 二、填空题 9.5 10. 1 3 11.30 12.2 100 13. 4 9 14. 1 3 三、解答题 15.(1)1 4 (2)1 6 (3)他通关的概率是1 6 . 16.解 (1)画出树状图如图: 由树状图可知共有 12 种等可能的结果,分别为 (1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3).每种结果出现的可能性相 同. (2)所有可能出现的结果共有 12 种,甲被选中的结果共有 6 种,即 P(甲被选中)= 6 12 = 1 2 . 17. 3 4 . 18.解 (1)根据题意知所有个位数字是 5 的“两位递增数”是 15,25,35,45 这 4 个. (2)画树状图如下: 可知共有 15 种等可能的结果,其中个位数字与十位数字之积能被 10 整除的结果有 3 种, 所以个位数字与十位数字之积能被 10 整除的概率为 3 15 = 1 5 . 19.解 (1)画树状图如下: 或列表如下: 甲 乙 6 7 8 9 3 9 10 11 12 4 10 11 12 13 5 11 12 13 14 (2)由(1)可知,两数之和共有 12 种等可能的情况,其中和小于 12 的情况有 6 种,和大于 12 的情况有 3 种,所以李燕获胜的概率为6 12 = 1 2 ,刘凯获胜的概率为 3 12 = 1 4