
第六章检测 一、选择题(每小题4分,共32分) 1下列式子中,①产②y是③0=k④=,⑤-忌能表示y是x的反比例函数的有() A.4个 B.3个 C.2个 D.1个 2已知电流(安培)、电压U(伏特)、电阻欧姆)之间的关系为1兴当电压为定值时/关于 R的函数图象是( 3如图,点A是反比例函数yx>0)图象上的一点,过点A作ACLy轴,垂足为点C,4C交反 比例函数的图象于点B,点P是x轴上的动点,则△PAB的面积为( A.2 B.4 C.6 D.8 4反比例函数的图象如图所示,以下结论:①常数m2,则1的值是( A.正数 B.负数 C.非正数 D.不能确定 6.如图,己知一次函数=+b和反比例函数y的图象相交于A(-2,),B12)两点,则不等式 ar+b1 7.如图,两个反比例函数二和=的图象分别是h和b.设点P在h上,PCLx轴,垂足为C 交h于点A,PDLy轴,垂足为D,交b于点B,则△PAB的面积为()
第六章检测 一、选择题(每小题 4 分,共 32 分) 1.下列式子中:①y= 𝑥 2 ;②y= 2 𝑥 ;③xy=k;④y=x-1 ;⑤y=- 2 3𝑥 ,能表示 y 是 x 的反比例函数的有( ). A.4 个 B.3 个 C.2 个 D.1 个 2.已知电流 I(安培)、电压 U(伏特)、电阻 R(欧姆)之间的关系为 I=𝑈 𝑅 ,当电压为定值时,I 关于 R 的函数图象是( ). 3.如图,点 A 是反比例函数 y= 6 𝑥 (x>0)图象上的一点,过点 A 作 AC⊥y 轴,垂足为点 C,AC 交反 比例函数 y= 2 𝑥的图象于点 B,点 P 是 x 轴上的动点,则△PAB 的面积为( ). A.2 B.4 C.6 D.8 4.反比例函数 y= 𝑚 𝑥的图象如图所示,以下结论:①常数 my2,则 x1-x2 的值是( ). A.正数 B.负数 C.非正数 D.不能确定 6.如图,已知一次函数 y=ax+b 和反比例函数 y= 𝑘 𝑥的图象相交于 A(-2,y1),B(1,y2)两点,则不等式 ax+b1 7.如图,两个反比例函数 y= 1 𝑥和 y=- 2 𝑥的图象分别是 l1 和 l2.设点 P 在 l1 上,PC⊥x 轴,垂足为 C, 交 l2 于点 A,PD⊥y 轴,垂足为 D,交 l2 于点 B,则△PAB 的面积为( )

A.3 B.4 c号 D.5 8.如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A,B两点,以AB为边在第 一象限内作正方形ABCD交反比例函数yk>0,xO)的图象于点D,将正方形ABCD沿x轴 负方向平移a个单位长度后得到正方形A'BCD,点C怡好落在反比例函数y>0,x>0)的 图象上,则a的值是() yk>0,x>0) y=-3x+3 0 D A.1 B.2 C.3 D.4 二、填空题(每小题4分,共24分) 9.反比例函数y一k+出的图象在每个象限内,函数值y随x值的增大而增大,则k的取值范围 是 10.王师傅用一根撬棒撬动一块大石头,己知阻力臂和阻力不变,分别为0.5m和1000N,当动 力臂1为2m时,撬动这块大石头需用的动力F为 11如图,点A在函数yx>0)的图象上,过点A作AB⊥x轴于点B,点C在线段AB上,且 BC:CA=1:2,函数)>0)的图象经过点C则k y 0 B 12.如图,点A是反比例函数图象上任意一点,过点A分别作x轴、y轴的垂线,垂足为 B,C,则四边形OBAC的面积为 13.如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点 P(3a,a)是反比例函数yk>0)的图象与正方形的一个交点若图中阴影部分的面积等于9,则 这个反比例函数的表达式为
A.3 B.4 C. 9 2 D.5 8.如图,在平面直角坐标系中,直线 y=-3x+3 与 x 轴、y 轴分别交于 A,B 两点,以 AB 为边在第 一象限内作正方形 ABCD 交反比例函数 y= 𝑘 𝑥 (k>0,x>0)的图象于点 D,将正方形 ABCD 沿 x 轴 负方向平移 a 个单位长度后得到正方形 A'B'C'D',点 C'恰好落在反比例函数 y= 𝑘 𝑥 (k>0,x>0)的 图象上,则 a 的值是( ). A.1 B.2 C.3 D.4 二、填空题(每小题 4 分,共 24 分) 9.反比例函数 y= 𝑘+1 𝑥 的图象在每个象限内,函数值 y 随 x 值的增大而增大,则 k 的取值范围 是 . 10.王师傅用一根撬棒撬动一块大石头,已知阻力臂和阻力不变,分别为 0.5 m 和 1 000 N,当动 力臂 l 为 2 m 时,撬动这块大石头需用的动力 F 为 . 11.如图,点 A 在函数 y= 6 𝑥 (x>0)的图象上,过点 A 作 AB⊥x 轴于点 B,点 C 在线段 AB 上,且 BC∶CA=1∶2,函数 y= 𝑘 𝑥 (x>0)的图象经过点 C,则 k= . 12.如图,点 A 是反比例函数 y= 3 𝑥 图象上任意一点,过点 A 分别作 x 轴、y 轴的垂线,垂足为 B,C,则四边形 OBAC 的面积为 . 13.如图,在平面直角坐标系中,正方形的中心在原点 O,且正方形的一组对边与 x 轴平行,点 P(3a,a)是反比例函数 y= 𝑘 𝑥 (k>0)的图象与正方形的一个交点.若图中阴影部分的面积等于 9,则 这个反比例函数的表达式为

14.已知在平面直角坐标系中有两点40,1),B1,0,动点P在反比例函数的图象上运动, 当线段PA与线段PB之差的绝对值最大时,点P的坐标为_ 三、解答题(共44分) 156分)已知反比例函数k为常数,0)的图象经过点42,3) (1)求这个函数的表达式: (2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由; (3)当-2<x<-1时,求y的取值范围. 16.(8分)已知正比例函数y=与反比例函数y的图象有一个公共点4(1,2) 0 (1)求这两个函数的表达式: (2)画出草图,根据图象写出正比例函数值大于反比例函数值时x的取值范围. 17.(10分)如图,已知边长为4的正方形ABCD中,AB⊥y轴,垂足为点E,AD⊥x轴,垂足为点F, 点A在反比例函数y-2的图象上,且点A的横坐标为1, y (1)请求出B,C两点的坐标; (2)线段BF,CE交于点G,求出点G到x轴的距离
14.已知在平面直角坐标系中有两点 A(0,1),B(-1,0),动点 P 在反比例函数 y= 2 𝑥的图象上运动, 当线段 PA 与线段 PB 之差的绝对值最大时,点 P 的坐标为 . 三、解答题(共 44 分) 15.(6 分)已知反比例函数 y= 𝑘 𝑥 (k 为常数,k≠0)的图象经过点 A(2,3). (1)求这个函数的表达式; (2)判断点 B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由; (3)当-2<x<-1 时,求 y 的取值范围. 16.(8 分)已知正比例函数 y=ax 与反比例函数 y= 𝑏 𝑥 的图象有一个公共点 A(1,2). (1)求这两个函数的表达式; (2)画出草图,根据图象写出正比例函数值大于反比例函数值时 x 的取值范围. 17.(10 分)如图,已知边长为 4 的正方形 ABCD 中,AB⊥y 轴,垂足为点 E,AD⊥x 轴,垂足为点 F, 点 A 在反比例函数 y= 2 𝑥 的图象上,且点 A 的横坐标为 1. (1)请求出 B,C 两点的坐标; (2)线段 BF,CE 交于点 G,求出点 G 到 x 轴的距离
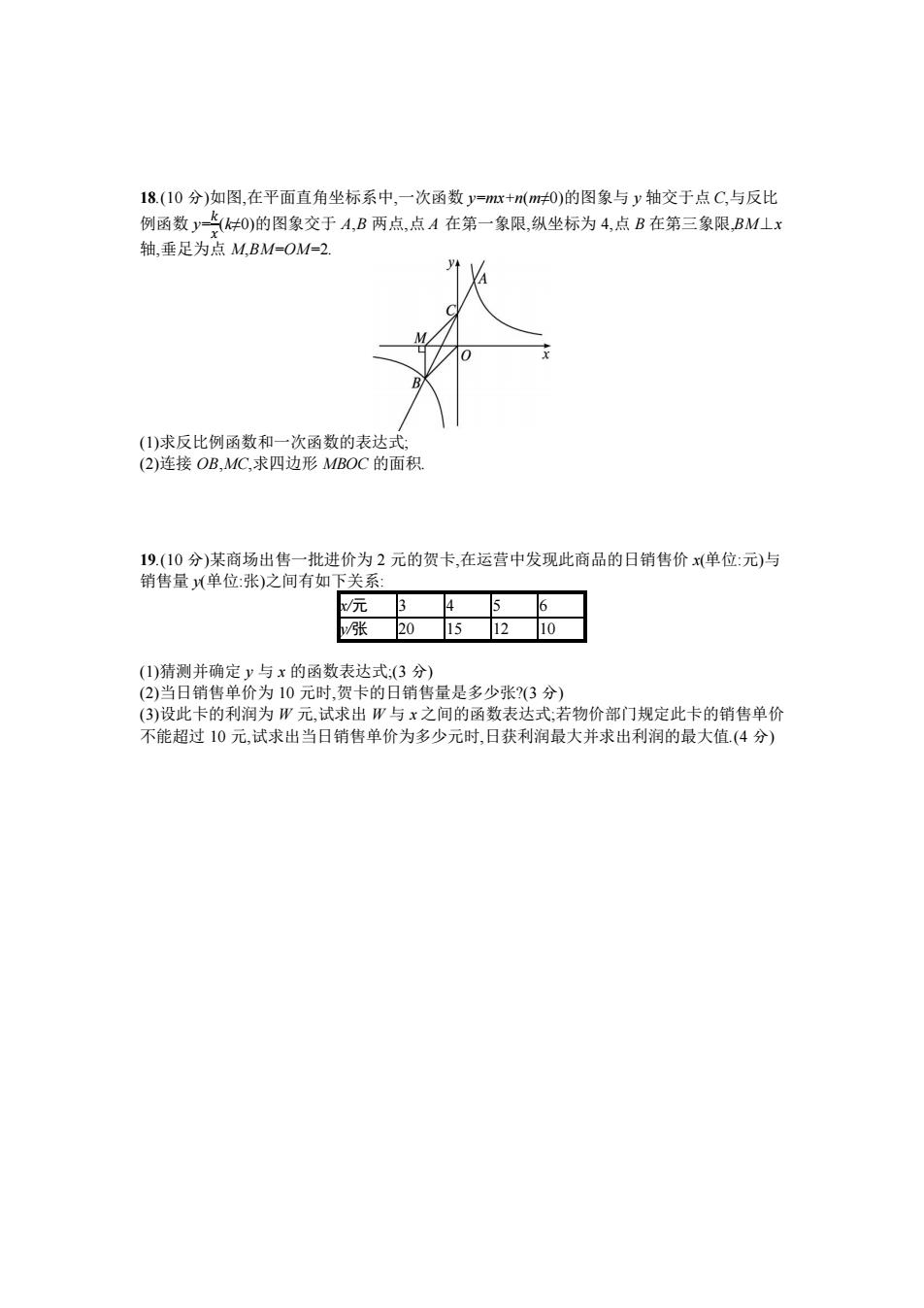
18.(10分)如图,在平面直角坐标系中,一次函数y=x+(m≠0)的图象与y轴交于点C,与反比 例函数y=(0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BMLx 轴,垂足为点M,BM=OM=2. (1)求反比例函数和一次函数的表达式, (2)连接OB,MC,求四边形MBOC的面积 19.(10分)某商场出售一批进价为2元的贺卡,在运营中发现此商品的日销售价x(单位:元)与 销售量单位:张)之间有如下关系: /元 3 4 6 张 20 1512 10 (1)猜测并确定y与x的函数表达式,(3分) (2)当日销售单价为10元时,贺卡的日销售量是多少张?(3分) (3)设此卡的利润为W元,试求出W与x之间的函数表达式;若物价部门规定此卡的销售单价 不能超过10元,试求出当日销售单价为多少元时,日获利润最大并求出利润的最大值.(4分)
18.(10 分)如图,在平面直角坐标系中,一次函数 y=mx+n(m≠0)的图象与 y 轴交于点 C,与反比 例函数 y= 𝑘 𝑥 (k≠0)的图象交于 A,B 两点,点 A 在第一象限,纵坐标为 4,点 B 在第三象限,BM⊥x 轴,垂足为点 M,BM=OM=2. (1)求反比例函数和一次函数的表达式; (2)连接 OB,MC,求四边形 MBOC 的面积. 19.(10 分)某商场出售一批进价为 2 元的贺卡,在运营中发现此商品的日销售价 x(单位:元)与 销售量 y(单位:张)之间有如下关系: x/元 3 4 5 6 y/张 20 15 12 10 (1)猜测并确定 y 与 x 的函数表达式;(3 分) (2)当日销售单价为 10 元时,贺卡的日销售量是多少张?(3 分) (3)设此卡的利润为 W 元,试求出 W 与 x 之间的函数表达式;若物价部门规定此卡的销售单价 不能超过 10 元,试求出当日销售单价为多少元时,日获利润最大并求出利润的最大值.(4 分)

第六章检测 一、选择题 1.B2.C3.A4.C5.D6.D7.C8.B 二、填空题 9kK110.250N1212.313y 14.(1,2)或(-2,-1) 三、解答题 15.解()起42,3)代入)兰得k=2×3=6, y (2)当x=】时y=6,:点B(-1,6)不在这个函数的图象上; 当x=3时y=2,:点C3,2)在这个函数的图象上 (3)当x=-1时y=6x=-2时y=-3 :当-2】或-1<x<0时,正比例函数值大于反比例函数值 17.解(①)对于y=2①,当x=1时y=2-2,故点A1,2),即AE=1,AF-2,则BE=ABAE=4- 1=3,FD=AD-AF=4-2=2,故点B的坐标为(-3,2),点C的坐标为(-3,-2) (2)迪()知,点F1,0),设直线BF的表达式为一+h则二3歌+b,解 k=- 0=k+b, 故直线 b=2 1 BF的表达式为y=字 设直线BF交y轴于点M,则点M(0,) 同理可得,直线CE的表达式为一字+2, 联立BF,CE的表达式并解得 x=-1 10 y=五 故点G的纵坐标为品则点G到x轴的距离为品 18.解(1):BM=OM=2 :点B的坐标为(-2,-2) :反比例函数y=k0)的图象经过点B -2=之解得k=4 :反比例函数的表达式为)兰
第六章检测 一、选择题 1.B 2.C 3.A 4.C 5.D 6.D 7.C 8.B 二、填空题 9.k1 或-1<x<0 时,正比例函数值大于反比例函数值. 17.解 (1)对于 y= 2 𝑥 ①,当 x=1 时,y= 2 𝑥 =2,故点 A(1,2),即 AE=1,AF=2,则 BE=AB-AE=4- 1=3,FD=AD-AF=4-2=2,故点 B 的坐标为(-3,2),点 C 的坐标为(-3,-2). (2)由(1)知,点 F(1,0),设直线 BF 的表达式为 y=kx+b,则{ 2 = -3𝑘 + 𝑏, 0 = 𝑘 + 𝑏, 解得{ 𝑘 = - 1 2 , 𝑏 = 1 2 , 故直线 BF 的表达式为 y=- 1 2 x+ 1 2 . 设直线 BF 交 y 轴于点 M,则点 M(0, 1 2 ), 同理可得,直线 CE 的表达式为 y= 4 3 x+2, 联立 BF,CE 的表达式并解得{ 𝑥 = - 9 11 , 𝑦 = 10 11 , 故点 G 的纵坐标为10 11 ,则点 G 到 x 轴的距离为10 11 . 18.解 (1)∵BM=OM=2, ∴点 B 的坐标为(-2,-2). ∵反比例函数 y= 𝑘 𝑥 (k≠0)的图象经过点 B, ∴-2= 𝑘 -2 ,解得 k=4. ∴反比例函数的表达式为 y= 4 𝑥

:点A的纵坐标为4, :4=4解得x=1. .:点A的坐标为(1,4) :·一次函数y=mx+n(m0)的图象经过点A1,4),B(-2,-2), 2n2解0 :一次函数的表达式为y=2x+2. (2)"一次函数y=2x+2的图象与y轴交于点C,:点C的坐标为(0,2).OC=BM=2 又BM⊥x轴,.:BM∥OC .:四边形MBOC为平行四边形 .:四边形MBOC的面积为OMOC=4 19.解(1)设y=k为常数,且k0),把点(3,20)代入,得=60, y与x的函数表达式是)x0) ②)当x=10时8=6:日销售单价为10元时,复卡的日销售量是6张 (6:W=t-2y-609 又x≤10.:当xl0时,W最大此时W=60器0-48(元
∵点 A 的纵坐标为 4, ∴4= 4 𝑥 ,解得 x=1. ∴点 A 的坐标为(1,4). ∵一次函数 y=mx+n(m≠0)的图象经过点 A(1,4),B(-2,-2), ∴{ 𝑚 + 𝑛 = 4, -2𝑚 + 𝑛 = -2, 解得{ 𝑚 = 2, 𝑛 = 2. ∴一次函数的表达式为 y=2x+2. (2)∵一次函数 y=2x+2 的图象与 y 轴交于点 C,∴点 C 的坐标为(0,2).∴OC=BM=2. 又 BM⊥x 轴,∴BM∥OC. ∴四边形 MBOC 为平行四边形. ∴四边形 MBOC 的面积为 OM·OC=4. 19.解 (1)设 y= 𝑘 𝑥 (k 为常数,且 k≠0),把点(3,20)代入,得 k=60, ∴y 与 x 的函数表达式是 y= 60 𝑥 (x>0). (2)当 x=10 时,y= 60 10 =6,∴日销售单价为 10 元时,贺卡的日销售量是 6 张. (3)∵W=(x-2)y=60- 120 𝑥 , 又 x≤10,∴当 x=10 时,W 最大,此时 W=60- 120 10 =48(元)