
24.1圆的有关性质 第1课时圆 ○素能.50. 0基础巩固 1.下列说法:①半圆是弧,但弧不一定是半圆:②半径相等的两个半圆是等弧:③张 度相等的两条弧是等弧;④凋长相等的圆是等圆;⑤面积相等的圆是等圆.其中正 确的个数是(C) A.2 B.3 C.4 D.5 2.以点O为圆心作圆,可以作(D) A.1个 B.2个 C.3个 D.无数个 3.下列命题中,正确的是(C), A.直径不是弦 B.半圆是直径和直径所对的弧组成的图形 C.圆中最长的弦是直径 D.一条弦所对的两条弧,不是优弧就是劣弧 4.如图 (1)线段OA.OB.OC是⊙O的半径;线段AB.AC.BC是⊙O的弦,其中最长的弦是 AC:ABBC是劣弧:ABC.AC是半圆, (2)若∠A=40°,则∠AB0=40°,∠C=50°,∠ABC=90° 。能力提升 5.若圆的半径为3,则弦AB长度的取值范围是0<AB<6
24.1 圆的有关性质 第 1 课时 圆 1.下列说法:①半圆是弧,但弧不一定是半圆;②半径相等的两个半圆是等弧;③长 度相等的两条弧是等弧;④周长相等的圆是等圆;⑤面积相等的圆是等圆.其中正 确的个数是(C). A.2 B.3 C.4 D.5 2.以点 O 为圆心作圆,可以作(D). A.1 个 B.2 个 C.3 个 D.无数个 3.下列命题中,正确的是(C). A.直径不是弦 B.半圆是直径和直径所对的弧组成的图形 C.圆中最长的弦是直径 D.一条弦所对的两条弧,不是优弧就是劣弧 4.如图. (1)线段 OA,OB,OC 是☉O 的半径;线段 AB,AC,BC 是☉O 的弦,其中最长的弦是 AC ; 𝐴𝐵⏜ ,𝐵𝐶⏜ 是劣弧; 𝐴𝐵𝐶 ⏜,𝐴𝐶⏜ 是半圆. (2)若∠A=40°,则∠ABO= 40° ,∠C= 50° ,∠ABC= 90° . 5.若圆的半径为 3,则弦 AB 长度的取值范围是 0<AB≤6

6.一个点到o0的最小距离为4cm,最大距离为9cm,则⊙O的半径是2.5cm或6.5 cm 7.如图,己知AC交⊙O于点A,B,且BC等于圆的半径,连接OC交⊙O于点 D,∠C=30°.求∠AOD的度数 答案:90° 第2课时 垂直于弦的直径 素能.50. 0基础巩固 1.如图,⊙O的直径为10cm,弦AB长为8cm,P是弦AB上一点,若OP的长为整数, 则满足条件的点P有(D), 1题图 A.2个 B.3个 C.4个 D.5个 2.如图,在⊙O中,AB,AC是互相垂直的两条弦,如果AB=8cm,AC=6cm,那么⊙O的 半径OA的长为(B) .0 2题图 A.4 cm B.5 cm C.6 cm D.8 cm
6.一个点到☉O的最小距离为4 cm,最大距离为9 cm,则☉O的半径是 2.5 cm或6.5 cm . 7.如图,已知 AC 交☉O 于点 A,B,且 BC 等于圆的半径,连接 OC 交☉O 于点 D,∠C=30°.求∠AOD 的度数. 答案:90° 第 2 课时 垂直于弦的直径 1.如图,☉O 的直径为 10 cm,弦 AB 长为 8 cm,P 是弦 AB 上一点,若 OP 的长为整数, 则满足条件的点 P 有(D). 1 题图 A.2 个 B.3 个 C.4 个 D.5 个 2.如图,在☉O 中,AB,AC 是互相垂直的两条弦,如果 AB=8 cm,AC=6 cm,那么☉O 的 半径 OA 的长为(B). 2 题图 A.4 cm B.5 cm C.6 cm D.8 cm

3.如图,在半径为5的⊙O中,若弦AB=8,则△AOB的面积为(C) A.24 B.16 C.12 D.8 3题图 4.如图,o0的半径为2,弦AB=2V3,点C在弦AB上,AC=AB,则OC的长为D), 4题图 A.V2 B.B.v3 c.c D.D 5.如图,⊙O过点B,C,圆心O在等腰直角三角形ABC的内 部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为(C) 5题图 A.10 B.B.23 C.C.13 D.D.3√2
3.如图,在半径为 5 的☉O 中,若弦 AB=8,则△AOB 的面积为(C). A.24 B.16 C.12 D.8 3 题图 4.如图,☉O 的半径为 2,弦 AB=2√3,点 C 在弦 AB 上,AC=1 4 AB,则 OC 的长为(D). 4 题图 A. √2 B. B.√3 C. C.2√3 3 D. D.√7 2 5.如图,☉O 过点 B,C,圆心 O 在等腰直角三角形 ABC 的内 部,∠BAC=90°,OA=1,BC=6,则☉O 的半径为(C). 5 题图 A. √10 B. B.2√3 C. C.√13 D. D.3√2

O能力提升 6.如图,在半径为10的⊙O中,OC垂直弦AB于点D,AB=16,则CD的长是4 7.己知⊙O的半径为13cm,AB,CD是⊙O的两条弦,且AB∥CD,AB=24cm,CD=10 cm,AB,CD之间的距离为多少? 解:根据题意可能会出现两种情况: ⊙ ② 当AB和CD在圆心O的同侧时, 如图①所示,过圆心O作OMLAB,垂足为M延长OM交CD于点N. 由AB∥CD,得ON⊥CD 由垂径定理,得BM=A=12cm, 2 DN-号-5cm由勾股定理,得: OM=√B02-BMZ=√132-12z=5(cm), 0N=vD02-DWz=√132-5z-12(cm. 所以MN=ON-OM=12-5=7(cm). 同理,当AB和CD在圆心O的异侧时, 如图②所示,可得MN=OM+ON=5+12=17(cm).所以AB,CD之间的距离为7cm或 17cm. 第3课时 弧、弦、圆心角 素能.达标螺 0基础巩固 1.⊙0的半径为6cm,一弦长为方程x2.5x-6=0的一个根,则圆心到该弦的距离和该 弦所对的圆心角为(D) A.V330°
6.如图,在半径为 10 的☉O 中,OC 垂直弦 AB 于点 D,AB=16,则 CD 的长是 4 . 7.已知☉O 的半径为 13 cm,AB,CD 是☉O 的两条弦,且 AB∥CD,AB=24 cm,CD=10 cm,AB,CD 之间的距离为多少? 解:根据题意可能会出现两种情况: ① ② 当 AB 和 CD 在圆心 O 的同侧时, 如图①所示,过圆心 O 作 OM⊥AB,垂足为 M,延长 OM 交 CD 于点 N. 由 AB∥CD,得 ON⊥CD. 由垂径定理,得 BM=𝐴𝐵 2 =12 cm, DN=𝐶𝐷 2 =5 cm.由勾股定理,得: OM=√𝐵𝑂2 -𝐵𝑀2=√13 2 -12 2=5(cm), ON=√𝐷𝑂2 -𝐷𝑁2=√13 2 -5 2=12(cm). 所以 MN=ON-OM=12-5=7(cm). 同理,当 AB 和 CD 在圆心 O 的异侧时, 如图②所示,可得 MN=OM+ON=5+12=17(cm).所以 AB,CD 之间的距离为 7 cm或 17 cm. 第 3 课时 弧、弦、圆心角 1.☉O 的半径为 6 cm,一弦长为方程 x 2 -5x-6=0 的一个根,则圆心到该弦的距离和该 弦所对的圆心角为(D). A.√3,30°

B.3V330° C.3.60° D.D.3V3,60° 2.如图,在⊙O中,如果AB=2CD,那么(A) A.AB>2CD B.AB<2CD C.AB=2CD D.AB与2CD的大小无法确定 3.如图,在⊙0中,弦AB=AC=5cmBC=8cm,则o0的半径等于若cm 3题图 4.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=3 4题图 0能力提升 5.如图,⊙O被△ABC三边所截得的弦长相等,∠A=70°,求∠BOC 解:如图,过点O作OMLAB,ON⊥AC,OP⊥BC,垂足分别为M,N,P. :∠A=70°, .:∠B+∠C=180°-∠A=110°
B.3√3,30° C. √3,60° D. D.3√3,60° 2.如图,在☉O 中,如果 AB=2CD,那么(A). A.𝐴𝐵⏜ >2𝐶𝐷⏜ B.𝐴𝐵⏜ <2𝐶𝐷⏜ C.𝐴𝐵⏜ =2𝐶𝐷⏜ D.𝐴𝐵⏜ 与 2𝐶𝐷⏜ 的大小无法确定 3.如图,在☉O 中,弦 AB=AC=5 cm,BC=8 cm,则☉O 的半径等于 25 6 cm. 3 题图 4.如图,AB 和 DE 是☉O 的直径,弦 AC∥DE,若弦 BE=3,则弦 CE=3 . 4 题图 5.如图,☉O 被△ABC 三边所截得的弦长相等,∠A=70°,求∠BOC. 解:如图,过点 O 作 OM⊥AB,ON⊥AC,OP⊥BC,垂足分别为 M,N,P. ∵∠A=70°, ∴∠B+∠C=180°-∠A=110°
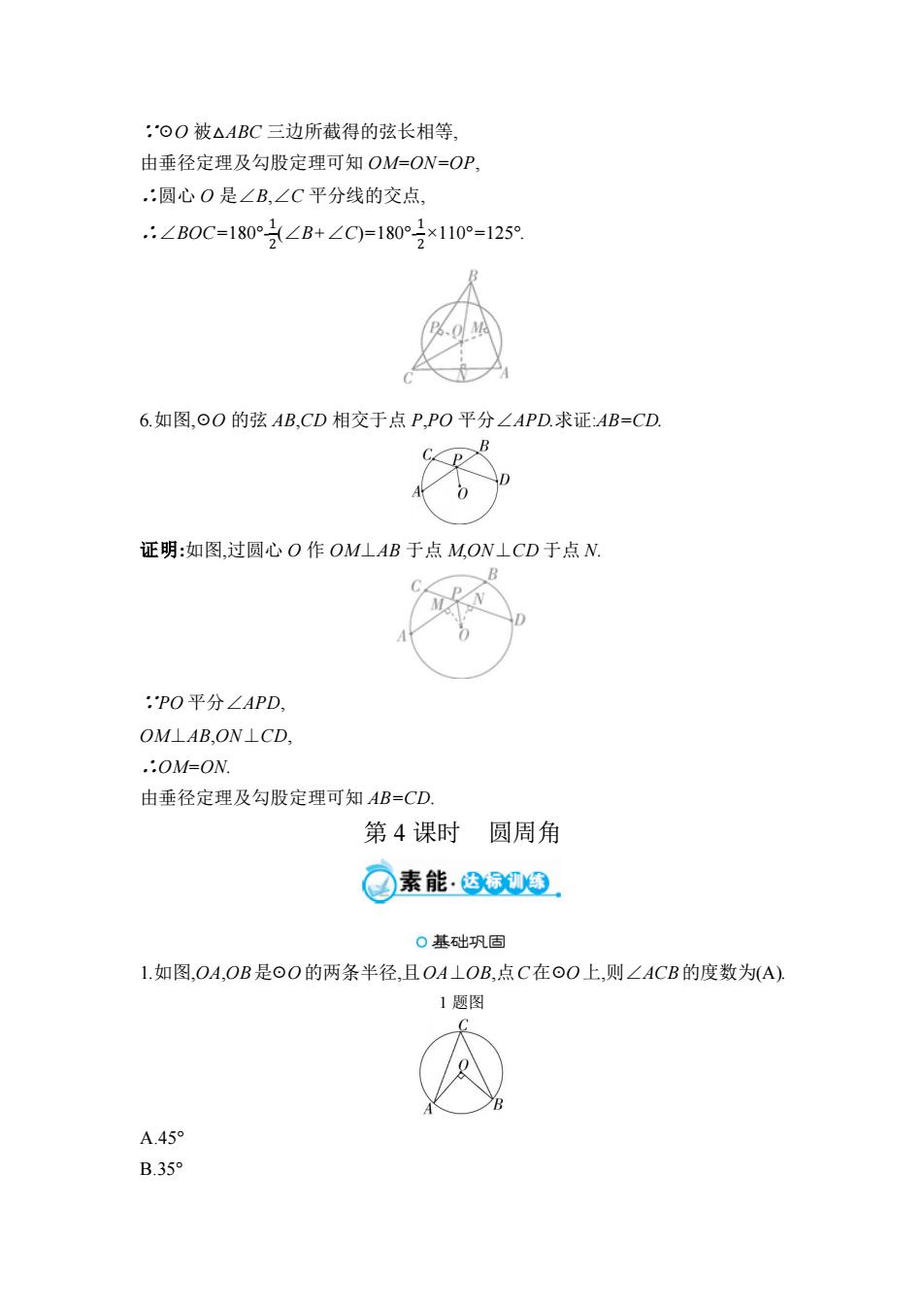
:⊙O被△ABC三边所截得的弦长相等, 由垂径定理及勾股定理可知OM=ON=OP, :圆心O是∠B,∠C平分线的交点 .:∠B0C=180°∠B+∠C=180°3×110°=1250 6.如图,⊙O的弦AB,CD相交于点P,PO平分∠APD.求证:AB=CD. B C P 证明:如图,过圆心O作OMLAB于点MON⊥CD于点N. B C :PO平分∠APD, OM⊥AB,ON⊥CD, .:OM=ON. 由垂径定理及勾股定理可知AB=CD 第4课时 圆周角 素能.达标划国, 0基础巩固 1.如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为(A) 1题图 A.45° B.35
∵☉O 被△ABC 三边所截得的弦长相等, 由垂径定理及勾股定理可知 OM=ON=OP, ∴圆心 O 是∠B,∠C 平分线的交点, ∴∠BOC=180°- 1 2 (∠B+∠C)=180°- 1 2 ×110°=125°. 6.如图,☉O 的弦 AB,CD 相交于点 P,PO 平分∠APD.求证:AB=CD. 证明:如图,过圆心 O 作 OM⊥AB 于点 M,ON⊥CD 于点 N. ∵PO 平分∠APD, OM⊥AB,ON⊥CD, ∴OM=ON. 由垂径定理及勾股定理可知 AB=CD. 第 4 课时 圆周角 1.如图,OA,OB是☉O的两条半径,且OA⊥OB,点C在☉O上,则∠ACB的度数为(A). 1 题图 A.45° B.35°

C.25° D.20° 2.如图,△ABC内接于⊙O,AC是⊙O的直径,已知∠C=50°,∠CBD=30°,则∠BAD的 度数是(B)】 2题图 A.45°B.70°C.90°D.95° 3.如图,在⊙O中,AB,AC是弦,点O在∠BAC的内部,若 ∠ABO=a,∠ACO=B,∠BOC=0,则下列关系中,正确的是(B) A.0=a+B B.0=2a+2f C.a+B+0=180° D.a+B+0=360° 4.如图所示,在⊙O中,∠ACB=∠D=60°,AC=3,则△ABC的周长为9 4题图 5.如图,在平面直角坐标系中,已知⊙C经过点O0,0),A0,2),B(2,0)点P是⊙C上的 一个动点(P与O,B不重合),则∠OCB的度数为90°,∠OPB的度数为45或 135° 5题图
C.25° D.20° 2.如图,△ABC 内接于☉O,AC 是☉O 的直径,已知∠C=50°,∠CBD=30°,则∠BAD 的 度数是(B). 2 题图 A.45° B.70° C.90° D.95° 3.如图,在☉O 中,AB,AC 是弦,点 O 在∠BAC 的内部,若 ∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系中,正确的是(B). A.θ=α+β B.θ=2α+2β C.α+β+θ=180° D.α+β+θ=360° 4.如图所示,在☉O 中,∠ACB=∠D=60°,AC=3,则△ABC 的周长为 9 . 4 题图 5.如图,在平面直角坐标系中,已知☉C 经过点 O(0,0),A(0,2),B(2,0).点 P 是☉C 上的 一个动点(P 与 O,B 不重合),则∠OCB 的度数为 90° ,∠OPB 的度数为 45°或 135° . 5 题图

。能力提升 6.如图,AB是⊙O的直径,点P为其半圆上任意一点(不与A,B重合),点Q为另外半 圆上一定点,若设∠POA=x,∠PQB=y,求y与x之间的函数解析式. 答案:y=90°0°<x<180) 7.如图,AB是⊙O的直径,CD⊥AB于点E,连接AD,OC (1)证明2∠D-∠C=90°: (2)若∠C=∠A,求∠D的度数, (1)证明::AB是⊙O的直径, CD⊥AB, :BC=BD,.:∠COB=2∠A, .:90°-∠C=2(90°-∠D), 即2∠D-∠C=90° (2)解::“∠C=∠A,:2∠D-∠A=90°,2∠D-(90°-∠D)=90°,解得∠D=60°
6.如图,AB 是☉O 的直径,点 P 为其半圆上任意一点(不与 A,B 重合),点 Q 为另外半 圆上一定点,若设∠POA=x,∠PQB=y,求 y 与 x 之间的函数解析式. 答案:y=90°- 𝑥 2 (0°<x<180°) 7.如图,AB 是☉O 的直径,CD⊥AB 于点 E,连接 AD,OC. (1)证明:2∠D-∠C=90°; (2)若∠C=∠A,求∠D 的度数. (1)证明:∵AB 是☉O 的直径, CD⊥AB, ∴𝐵𝐶⏜ =𝐵𝐷⏜ ,∴∠COB=2∠A, ∴90°-∠C=2(90°-∠D), 即 2∠D-∠C=90°. (2)解:∵∠C=∠A,∴2∠D-∠A=90°,2∠D-(90°-∠D)=90°,解得∠D=60°