
期末检测 一、选择题(每小题3分,共30分) 1.下列对二次函数y=x2-x的图象的描述,正确的是( A.开口向下 B.对称轴是y轴 C经过原点 D.在对称轴右侧部分是下降的 2.已知⊙O的半径为4,圆心到点P的距离为d,且d是方程x2-2x-8=0的根,则点P 与⊙0的位置关系是() A.点P在⊙O内部 B.点P在⊙O上 C.点P在⊙O外部 D.无法确定 3.在平面直角坐标系中,将抛物线y=(x+1)P向右平移2个单位长度,再向下平移4 个单位长度,得到的抛物线的表达式是() A.y=(x-2)2-4 By=(x-12-4 Cy=(x-2)2-3 Dy=(x-12-3 4.身高相同的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线 与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是 同学 甲 丙 放出风 筝线长 140m 100m 95m 90m 线与地 30° 45 45 609 面夹角 A.甲 B.乙 c丙 D.丁 5.在△ABC中,若sinA.+(-tanB=0,∠A,∠B都是锐角,则∠C的度数是 ()方 A.75° B.90 C.105 D.120° 6一次函数)会+e的图象如图所示,则二次函数=a2+x+c在平面直角坐标系 中的图象可能是( 7.如图,AB是⊙O的直径,弦CD⊥OA于点E,连接OC,OD.若⊙O的半径为m, ∠AOD=∠α,则下列结论一定成立的是()
期末检测 一、选择题(每小题 3 分,共 30 分) 1.下列对二次函数 y=x2 -x 的图象的描述,正确的是( ). A.开口向下 B.对称轴是 y 轴 C.经过原点 D.在对称轴右侧部分是下降的 2.已知☉O 的半径为 4,圆心到点 P 的距离为 d,且 d 是方程 x 2 -2x-8=0 的根,则点 P 与☉O 的位置关系是( ). A.点 P 在☉O 内部 B.点 P 在☉O 上 C.点 P 在☉O 外部 D.无法确定 3.在平面直角坐标系中,将抛物线 y=(x+1)2 向右平移 2 个单位长度,再向下平移 4 个单位长度,得到的抛物线的表达式是( ). A.y=(x-2)2 -4 B.y=(x-1)2 -4 C.y=(x-2)2 -3 D.y=(x-1)2 -3 4.身高相同的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线 与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是 ( ). 同学 甲 乙 丙 丁 放出风 筝线长 140 m 100 m 95 m 90 m 线与地 面夹角 30° 45° 45° 60° A.甲 B.乙 C.丙 D.丁 5.在△ABC 中,若|sin𝐴- √2 2 |+( √3 3 − tan 𝐵) 2=0,∠A,∠B 都是锐角,则∠C 的度数是 ( ). A.75° B.90° C.105° D.120° 6.一次函数 y= 𝑏 𝑎 x+c 的图象如图所示,则二次函数 y=ax2+bx+c 在平面直角坐标系 中的图象可能是( ). 7.如图,AB 是☉O 的直径,弦 CD⊥OA 于点 E,连接 OC,OD.若☉O 的半径为 m, ∠AOD=∠α,则下列结论一定成立的是( )

D A.OE=mtana B.CD=2msin a C.AE=m'cosa D.SacoD-m2-sin a 8.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接 BD,若cOs∠BDC-5则BC的长是( A.10 B.8 C.43 D.2√6 9.若对于任意非零实数a,抛物线y=ax2+ax-2a总不经过点P(xo-3,x-16),则符合条 件的点P( A.有且只有1个B.有且只有2个 C.有且只有3个D.有无穷多个 10.如图,⊙A过点O0,0),C(N3,0),D0,1),点B是x轴下方⊙A上的一点,连接 BO,BD,则∠OBD的度数是( y A A.15 B.30° C.45° D.60° 二、填空题(每小题4分,共24分) 11.在直角三角形ABC中,若2AB=AC,则cosC= 12.如图,已知⊙0的半径为1,点P是⊙0外一点,且OP=2.若PT是⊙0的切线,T 为切点,连接OT,则PT=」 13.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的 半径为2,则CD的长为
A.OE=m·tan α B.CD=2m·sin α C.AE=m·cos α D.S△COD= 1 2 m2·sin α 8.如图,在△ABC 中,∠C=90°,AC=12,AB 的垂直平分线 EF 交 AC 于点 D,连接 BD,若 cos∠BDC=5 7 ,则 BC 的长是( ). A.10 B.8 C.4√3 D.2√6 9.若对于任意非零实数 a,抛物线 y=ax2+ax-2a 总不经过点 P(x0-3,𝑥0 2 -16),则符合条 件的点 P( ). A.有且只有 1 个 B.有且只有 2 个 C.有且只有 3 个 D.有无穷多个 10.如图,☉A 过点 O(0,0),C(√3,0),D(0,1),点 B 是 x 轴下方☉A 上的一点,连接 BO,BD,则∠OBD 的度数是( ). A.15° B.30° C.45° D.60° 二、填空题(每小题 4 分,共 24 分) 11.在直角三角形 ABC 中,若 2AB=AC,则 cos C= . 12.如图,已知☉O 的半径为 1,点 P 是☉O 外一点,且 OP=2.若 PT 是☉O 的切线,T 为切点,连接 OT,则 PT= . 13.如图,△ABC 内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB 于点 D,若☉O 的 半径为 2,则 CD 的长为
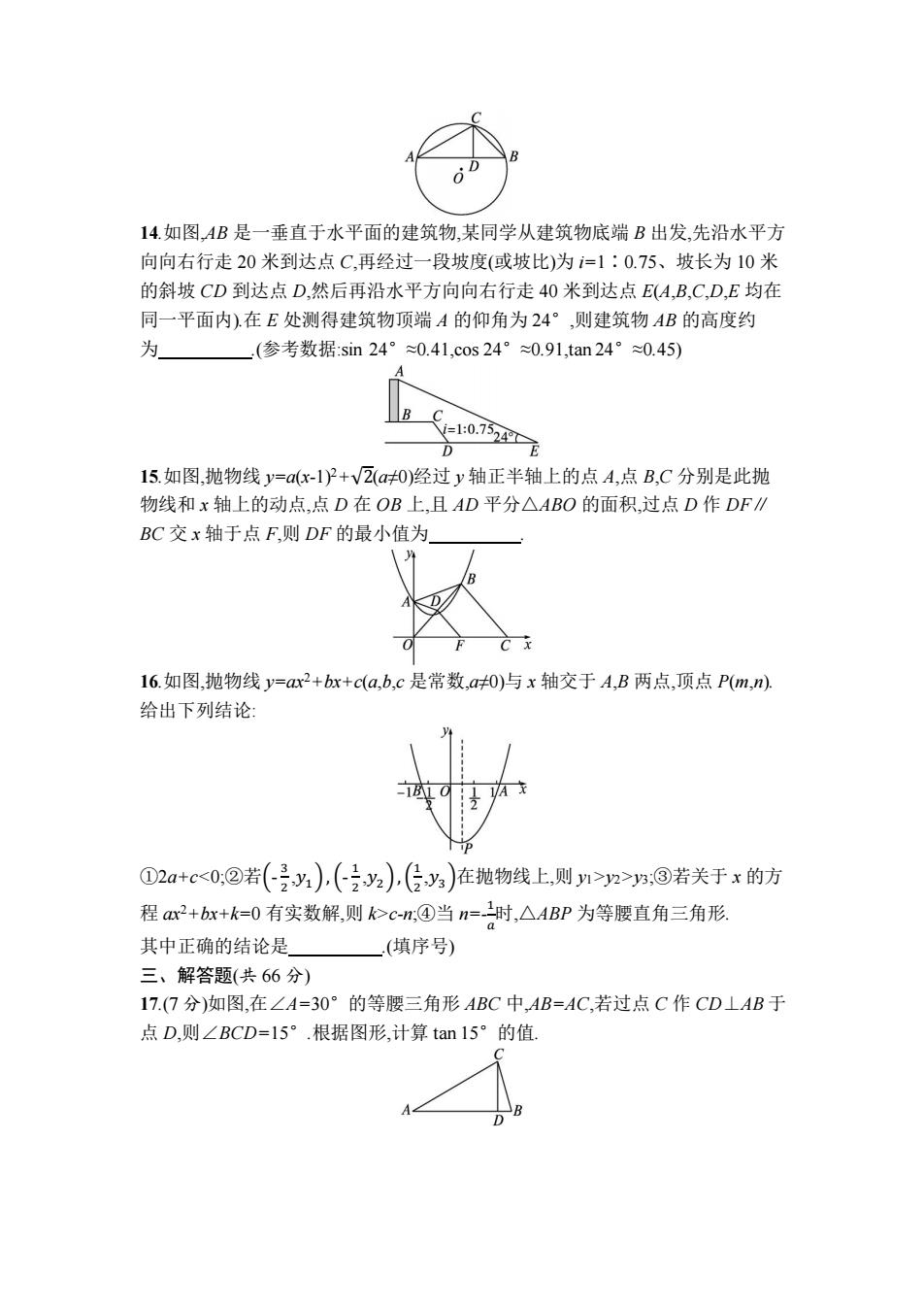
14.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方 向向右行走20米到达点C,再经过一段坡度(或坡比)为=1:0.75、坡长为10米 的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在 同一平面内)在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约 为 (参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45) i=1:0.75249℃ D 15.如图,抛物线y=a(x-1)2+V2(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛 物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过点D作DF∥ BC交x轴于点F,则DF的最小值为 16.如图,抛物线y=ar2+br+c(a,b,c是常数,a0)与x轴交于A,B两点,顶点P(m,n), 给出下列结论: ①2a+c2>,③若关于x的方 程ar2+bx+k=0有实数解,则k>c-n;④当n=时,△ABP为等腰直角三角形 其中正确的结论是 .(填序号) 三、解答题(共66分) 17.(7分)如图,在∠A=30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于 点D,则∠BCD=l5°.根据图形,计算tan15°的值
14.如图,AB 是一垂直于水平面的建筑物,某同学从建筑物底端 B 出发,先沿水平方 向向右行走 20 米到达点 C,再经过一段坡度(或坡比)为 i=1∶0.75、坡长为 10 米 的斜坡 CD 到达点 D,然后再沿水平方向向右行走 40 米到达点 E(A,B,C,D,E 均在 同一平面内).在 E 处测得建筑物顶端 A 的仰角为 24°,则建筑物 AB 的高度约 为 .(参考数据:sin 24°≈0.41,cos 24°≈0.91,tan 24°≈0.45) 15.如图,抛物线 y=a(x-1)2+√2(a≠0)经过 y 轴正半轴上的点 A,点 B,C 分别是此抛 物线和 x 轴上的动点,点 D 在 OB 上,且 AD 平分△ABO 的面积,过点 D 作 DF∥ BC 交 x 轴于点 F,则 DF 的最小值为 . 16.如图,抛物线 y=ax2+bx+c(a,b,c 是常数,a≠0)与 x 轴交于 A,B 两点,顶点 P(m,n). 给出下列结论: ①2a+cy2>y3;③若关于 x 的方 程 ax2+bx+k=0 有实数解,则 k>c-n;④当 n=- 1 𝑎时,△ABP 为等腰直角三角形. 其中正确的结论是 .(填序号) 三、解答题(共 66 分) 17.(7 分)如图,在∠A=30°的等腰三角形 ABC 中,AB=AC,若过点 C 作 CD⊥AB 于 点 D,则∠BCD=15°.根据图形,计算 tan 15°的值

18.(7分)五一劳动节期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接 到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的 绿道1步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向, 如图所示.根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走 多少米才能到达桥头D处?(结果精确到1米)参考数据√2≈1.414,V3≈1.732) 你只要沿着绿道继续 直走就可以看到我, 在正南方的桥头D处 小陈,我已经到达B处了 我就在那里接你. 19.(9分)已知关于x的一元二次方程(m-1)x2+(m-2)x-1=0(m为实数) (1)若方程有两个不相等的实数根,求m的取值范围: (2)若号是此方程的实数根,抛物线y=(m-1)x2+(m-2)x-1与x轴交于A,B两点,抛物 线的顶点为C,求△ABC的面积. 20.(9分)某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是 200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台, 且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低 于300元/台,代理销售商每月要完成不低于450台的销售任务 (I)试确定月销售量(台)与售价x(元/台)之间的函数表达式,并求出自变量x的取 值范围; (2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润(元) 最大?最大利润是多少? 21.(11分)如图,AB是⊙O的直径,点C是⊙O上一点(与点A,B不重合),过点C作 直线PO,使得∠ACQ=∠ABC (1)求证:直线PQ是⊙O的切线: 2)过点A作AD⊥PQ于点D,交o0于点E,若⊙0的半径为2,sin∠DAC=三求图 中阴影部分的面积 22.(11分2022贵州毕节中考)如图,在△ABC中,∠ACB=90°,D是AB边上一点, 以BD为直径的⊙O与AC相切于点E,连接DE并延长交BC的延长线于点F
18.(7 分)五一劳动节期间,小明到小陈家所在的美丽乡村游玩,在村头 A 处小明接 到小陈发来的定位,发现小陈家 C 在自己的北偏东 45°方向,于是沿河边笔直的 绿道 l 步行 200 米到达 B 处,这时定位显示小陈家 C 在自己的北偏东 30°方向, 如图所示.根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走 多少米才能到达桥头 D 处?(结果精确到 1 米)(参考数据:√2≈1.414,√3≈1.732) 19.(9 分)已知关于 x 的一元二次方程(m-1)x 2+(m-2)x-1=0(m 为实数). (1)若方程有两个不相等的实数根,求 m 的取值范围; (2)若 1 2 是此方程的实数根,抛物线 y=(m-1)x 2+(m-2)x-1 与 x 轴交于 A,B 两点,抛物 线的顶点为 C,求△ABC 的面积. 20.(9 分)某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是 200 元/台.经过市场销售后发现:在一个月内,当售价是 400 元/台时,可售出 200 台, 且售价每降低 10 元,就可多售出 50 台.若供货商规定这种空气净化器售价不能低 于 300 元/台,代理销售商每月要完成不低于 450 台的销售任务. (1)试确定月销售量 y(台)与售价 x(元/台)之间的函数表达式,并求出自变量 x 的取 值范围; (2)当售价 x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润 w(元) 最大?最大利润是多少? 21.(11 分)如图,AB 是☉O 的直径,点 C 是☉O 上一点(与点 A,B 不重合),过点 C 作 直线 PQ,使得∠ACQ=∠ABC. (1)求证:直线 PQ 是☉O 的切线; (2)过点 A 作 AD⊥PQ 于点 D,交☉O 于点 E,若☉O 的半径为 2,sin∠DAC=1 2 ,求图 中阴影部分的面积. 22.(11 分)(2022·贵州毕节中考)如图,在△ABC 中,∠ACB=90°,D 是 AB 边上一点, 以 BD 为直径的☉O 与 AC 相切于点 E,连接 DE 并延长交 BC 的延长线于点 F

(I)求证:BF=BD: (2)若CF=1,tan∠EDB=2,求⊙O的直径. 23.(12分)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B, 与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D. AID/B (1)求二次函数的表达式: (2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在,请求出点P的坐标, (3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个 点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动 当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,△MNB的面 积最大?试求出最大面积 答案: 一、选择题 1.C2.B3.B4.D5.C6.A7.B8.D9.B10.B 二、填空题 119或2g12V313V21421.7米15号16.②@ 三、解答题 17.解:.AB=AC,∴.可设AB=AC=2x .∠A=30°,CD⊥AB, ∴CD=24C=x .AD2+CD2=AC2 ∴AD=√AC2-CDz=J(2x2-x2=V3x ..BD=AB-AD=2x-V3x=(2-V3x tan15°_e=2-v3-2-V3 CD 18.解:由题意可得,∠CAD=45°,∠CBD=60°,AB=200米 设BD=x米,则DC=V3x米
(1)求证:BF=BD; (2)若 CF=1,tan∠EDB=2,求☉O 的直径. 23.(12 分)如图,关于 x 的二次函数 y=x2+bx+c 的图象与 x 轴交于点 A(1,0)和点 B, 与 y 轴交于点 C(0,3),抛物线的对称轴与 x 轴交于点 D. (1)求二次函数的表达式; (2)在 y 轴上是否存在一点 P,使△PBC 为等腰三角形?若存在,请求出点 P 的坐标; (3)有一个点 M 从点 A 出发,以每秒 1 个单位的速度在 AB 上向点 B 运动,另一个 点 N 从点 D 与点 M 同时出发,以每秒 2 个单位的速度在抛物线的对称轴上运动, 当点 M 到达点 B 时,点 M,N 同时停止运动,问点 M,N 运动到何处时,△MNB 的面 积最大?试求出最大面积. 答案: 一、选择题 1.C 2.B 3.B 4.D 5.C 6.A 7.B 8.D 9.B 10.B 二、填空题 11. √3 2 或 2√5 5 12.√3 13.√2 14.21.7 米 15. √2 2 16.②④ 三、解答题 17.解:∵AB=AC,∴可设 AB=AC=2x. ∵∠A=30°,CD⊥AB, ∴CD=1 2 AC=x. ∵AD2+CD2=AC2 , ∴AD=√𝐴𝐶 2 -𝐶𝐷2 = √(2𝑥) 2 -𝑥 2 = √3x. ∴BD=AB-AD=2x-√3x=(2-√3)x. ∴tan 15°= 𝐵𝐷 𝐶𝐷 = (2-√3)𝑥 𝑥 =2-√3. 18.解:由题意可得,∠CAD=45°,∠CBD=60°,AB=200 米. 设 BD=x 米,则 DC=√3x 米

.AD=DC, ∴.200+x=V3x, 解得x=100(√3+1))273(米)】 ∴.小明还需沿绿道继续直走273米才能到达桥头D处 19.解:(1)根据题意,得4=(m-22-4×(m-1)×(-1)>0,即m2>0,解得m>0或m0(m≠1)】 (2)之是此方程的实数根, ∴(m-l)×+(m-2)×31=0,解得m=3. “抛物线的表达式为y=2x2+x1=2(x+)- “顶点C的坐标为(》 令y=0,得2x2+x-1=0, 解得x=1或号 ∴AB=1引=月 .S0x2×名=器 20.解:(1)根据题中条件,销售价每降低10元,就可多售出50台,则月销售量台) 与售价x(元/合)之间的函数表达式为y=200+50×400x=-5x+2200. 10 供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低 于450台的销售任务 则≥300, -5x+2200≥450 解得300≤x≤350 y与x之间的函数表达式为y=-5x+2200(300≤x≤350) (2)w=(x-200(-5x+2200)=-5(x-320)2+72000. ,x=320在300≤x≤350内, ∴.当x=320时,最大值为72000. ∴.售价定为320元/怡时,商场每月销售这种空气净化器所获得的利润w最大,最 大利润是72000元. 21.(1)证明如图,连接OC, ,AB是⊙O的直径 .∠ACB=90°
∵AD=DC, ∴200+x=√3x, 解得 x=100(√3+1)≈273(米). ∴小明还需沿绿道继续直走 273 米才能到达桥头 D 处. 19.解:(1)根据题意,得 Δ=(m-2)2 -4×(m-1)×(-1)>0,即 m2>0,解得 m>0 或 m0(m≠1). (2)∵ 1 2是此方程的实数根, ∴(m-1)×( 1 2 ) 2 +(m-2)× 1 2 -1=0,解得 m=3. ∴抛物线的表达式为 y=2x 2+x-1=2(𝑥 + 1 4 ) 2 − 9 8 . ∴顶点 C 的坐标为(- 1 4 ,- 9 8 ). 令 y=0,得 2x 2+x-1=0, 解得 x=-1 或 1 2 . ∴AB=|-1- 1 2 | = 3 2 . ∴S△ABC= 1 2 × 3 2 × 9 8 = 27 32 . 20.解:(1)根据题中条件,销售价每降低 10 元,就可多售出 50 台,则月销售量 y(台) 与售价 x(元/台)之间的函数表达式为 y=200+50× 400-𝑥 10 =-5x+2 200. 供货商规定这种空气净化器售价不能低于 300 元/台,代理销售商每月要完成不低 于 450 台的销售任务, 则{ 𝑥 ≥ 300, -5𝑥 + 2 200 ≥ 450, 解得 300≤x≤350. ∴y 与 x 之间的函数表达式为 y=-5x+2 200(300≤x≤350). (2)w=(x-200)(-5x+2 200)=-5(x-320)2+72 000. ∵x=320 在 300≤x≤350 内, ∴当 x=320 时,最大值为 72 000. ∴售价定为 320 元/台时,商场每月销售这种空气净化器所获得的利润 w 最大,最 大利润是 72 000 元. 21.(1)证明 如图,连接 OC, ∵AB 是☉O 的直径, ∴∠ACB=90°

.OA=OC. .∠CAB=∠ACO :∠ACQ=∠ABC, ∴.∠CAB+∠ABC=∠ACO+∠ACQ=∠OCQ=90°,即OC⊥PQ ∴.直线PQ是⊙O的切线 (2)解:连接OE, .sin∠DAC=1,AD⊥PQ, .∠DAC=30°,∠ACD=60°. ∴.∠ABC=∠ACD=60°, ∴.∠CAB=90°-60°=30° ∴.∠EAO=∠DAC+∠CAB=60° 又OA=OE,∴.△AE0为等边三角形,∴.∠AOE=60°. ∴.S阴影=S扇形AOE-S△4EO =Sa鞯40E20A-OE-sin60° =0m×22×2×2×写 360 -2亚-3 3 “图中阴影部分的面积为红-V3 22.(1)证明连接OE,如图(1), 图(1) AC是⊙O的切线 .OE⊥AC ,AC⊥BC ∴.OE∥BC ∴.∠OED=∠F. .OD=OE. ∴.∠ODE=∠OED .∠BDE=∠F ∴.BF=BD (2)解:连接BE,如图(2)
∵OA=OC, ∴∠CAB=∠ACO. ∵∠ACQ=∠ABC, ∴∠CAB+∠ABC=∠ACO+∠ACQ=∠OCQ=90°,即 OC⊥PQ, ∴直线 PQ 是☉O 的切线. (2)解:连接 OE, ∵sin∠DAC=1 2 ,AD⊥PQ, ∴∠DAC=30°,∠ACD=60°. ∴∠ABC=∠ACD=60°, ∴∠CAB=90°-60°=30°, ∴∠EAO=∠DAC+∠CAB=60°. 又 OA=OE,∴△AEO 为等边三角形,∴∠AOE=60°. ∴S 阴影=S 扇形 AOE-S△AEO =S 扇形 AOE- 1 2 OA·OE·sin 60° = 60π 360 ×2 2 - 1 2 ×2×2× √3 2 = 2π 3 − √3. ∴图中阴影部分的面积为2π 3 − √3. 22.(1)证明 连接 OE,如图(1), 图(1) ∵AC 是☉O 的切线, ∴OE⊥AC. ∵AC⊥BC, ∴OE∥BC. ∴∠OED=∠F. ∵OD=OE, ∴∠ODE=∠OED. ∴∠BDE=∠F. ∴BF=BD. (2)解:连接 BE,如图(2)

图(2) ,∠BDE=∠F, .∴.tan∠BDE=tan∠F=2. :Cf=l,ian∠Fg ∴.CE=2 .BD是⊙O的直径 ∴.∠BED=90°. ∴.BE⊥EF ,EC⊥BF ∴.△ECF∽△BCE. 器=器 ..EC2=BC.CF. ∴.BC=4 ∴.BF=BC+CF=5. ..BD=BF=5. 即⊙O的直径为5. 23.解:(1)把A(1,0)和C0,3)代入y=x2+bx+C, 限±8+e=0 解得化二 .二次函数的表达式为y=x24x+3. (2)令y=0,则x2-4x+3=0, 解得x=1或x=3. .B(3,0).∴.BC=3V2 点P在y轴上,当△PBC为等腰 三角形时,分三种情况进行讨论,如图
图(2) ∵∠BDE=∠F, ∴tan∠BDE=tan∠F=2. ∵CF=1,tan∠F=𝐶𝐸 𝐶𝐹 , ∴CE=2. ∵BD 是☉O 的直径, ∴∠BED=90°. ∴BE⊥EF. ∵EC⊥BF, ∴△ECF∽△BCE. ∴ 𝐸𝐶 𝐶𝐹 = 𝐵𝐶 𝐸𝐶 . ∴EC2=BC·CF. ∴BC=4. ∴BF=BC+CF=5. ∴BD=BF=5, 即☉O 的直径为 5. 23.解:(1)把 A(1,0)和 C(0,3)代入 y=x2+bx+c, 得{ 1 + 𝑏 + 𝑐 = 0, 𝑐 = 3, 解得{ 𝑏 = -4, 𝑐 = 3. ∴二次函数的表达式为 y=x2 -4x+3. (2)令 y=0,则 x 2 -4x+3=0, 解得 x=1 或 x=3. ∴B(3,0).∴BC=3√2. 点 P 在 y 轴上,当△PBC 为等腰 三角形时,分三种情况进行讨论,如图

(PA P ①当CP=CB时,PC=3VZ ∴.OP=OC+PC=3+3vVz或OP=PC-OC=3V2-3 .P1(0,3+3v√2),P2(0,3-3V2: ②当BP=BC时,OP=OB=3, ∴.P3(0,-3) ③当PB=PC时,,OC=OB=3, .此时P与0重合,P4(0,0) 综上所述,点P的坐标为(0,3+3V2或(0,3-3V②或(0,-3)或(0,0) (3)设M运动时间为1,由AB=2,得BM=2-1,则DN-2L, SaB=×2-0×21=-R+21=-IP+1 .当M2,0),N(2,2)或(2,-2)时,△NB的面积最大,最大面积是1
①当 CP=CB 时,PC=3√2, ∴OP=OC+PC=3+3√2或 OP=PC-OC=3√2-3, ∴P1(0,3+3√2),P2(0,3-3√2); ②当 BP=BC 时,OP=OB=3, ∴P3(0,-3); ③当 PB=PC 时,∵OC=OB=3, ∴此时 P 与 O 重合,∴P4(0,0). 综上所述,点 P 的坐标为(0,3+3√2)或(0,3-3√2)或(0,-3)或(0,0). (3)设 M 运动时间为 t,由 AB=2,得 BM=2-t,则 DN=2t, ∴S△MNB= 1 2 ×(2-t)×2t=-t 2+2t=-(t-1)2+1. ∴当 M(2,0),N(2,2)或(2,-2)时,△MNB 的面积最大,最大面积是 1