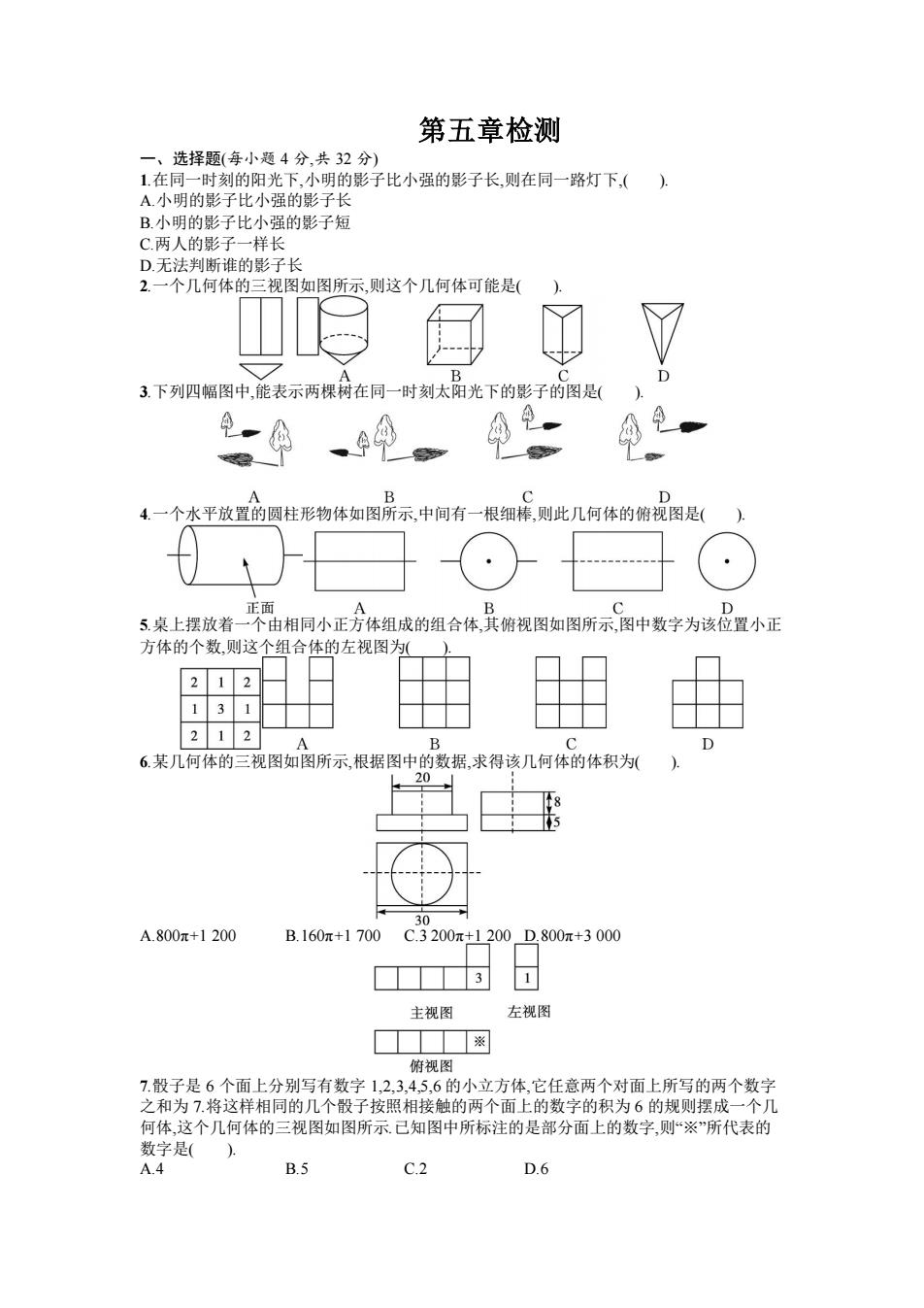
第五章检测 一、选择题(每小题4分,共32分) 1在同一时刻的阳光下,小明的影子比小强的影子长,则在同一路灯下,() A.小明的影子比小强的影子长 B.小明的影子比小强的影子短 C两人的影子一样长 D.无法判断谁的影子长 2.一个几何体的三视图如图所示,则这个几何体可能是( ☑ 3.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( 4.一个水平放置的圆柱形物体如图所示,中间有一根细棒,则此几何体的俯视图是( 正面 D 5.桌上摆放着一个由相同小正方体组成的组合体其俯视图如图所示,图中数字为该位置小正 方体的个数,则这个组合体的左视图为( 212 A B C D 6.某几何体的三视图如图所示,根据图中的数据,求得该几何体的体积为( 20 30 A.800元+1200 B.160π+1700 C.3200π+1200D.800元+3000 3 主视图 左视图 ※ 俯视图 7.骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两个对面上所写的两个数字 之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6的规则摆成一个几 何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字则“※”所代表的 数字是()。 A.4 B.5 C.2 D.6
第五章检测 一、选择题(每小题 4 分,共 32 分) 1.在同一时刻的阳光下,小明的影子比小强的影子长,则在同一路灯下,( ). A.小明的影子比小强的影子长 B.小明的影子比小强的影子短 C.两人的影子一样长 D.无法判断谁的影子长 2.一个几何体的三视图如图所示,则这个几何体可能是( ). 3.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( ). 4.一个水平放置的圆柱形物体如图所示,中间有一根细棒,则此几何体的俯视图是( ). 5.桌上摆放着一个由相同小正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正 方体的个数,则这个组合体的左视图为( ). 6.某几何体的三视图如图所示,根据图中的数据,求得该几何体的体积为( ). A.800π+1 200 B.160π+1 700 C.3 200π+1 200 D.800π+3 000 7.骰子是 6 个面上分别写有数字 1,2,3,4,5,6 的小立方体,它任意两个对面上所写的两个数字 之和为 7.将这样相同的几个骰子按照相接触的两个面上的数字的积为 6 的规则摆成一个几 何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“※”所代表的 数字是( ). A.4 B.5 C.2 D.6
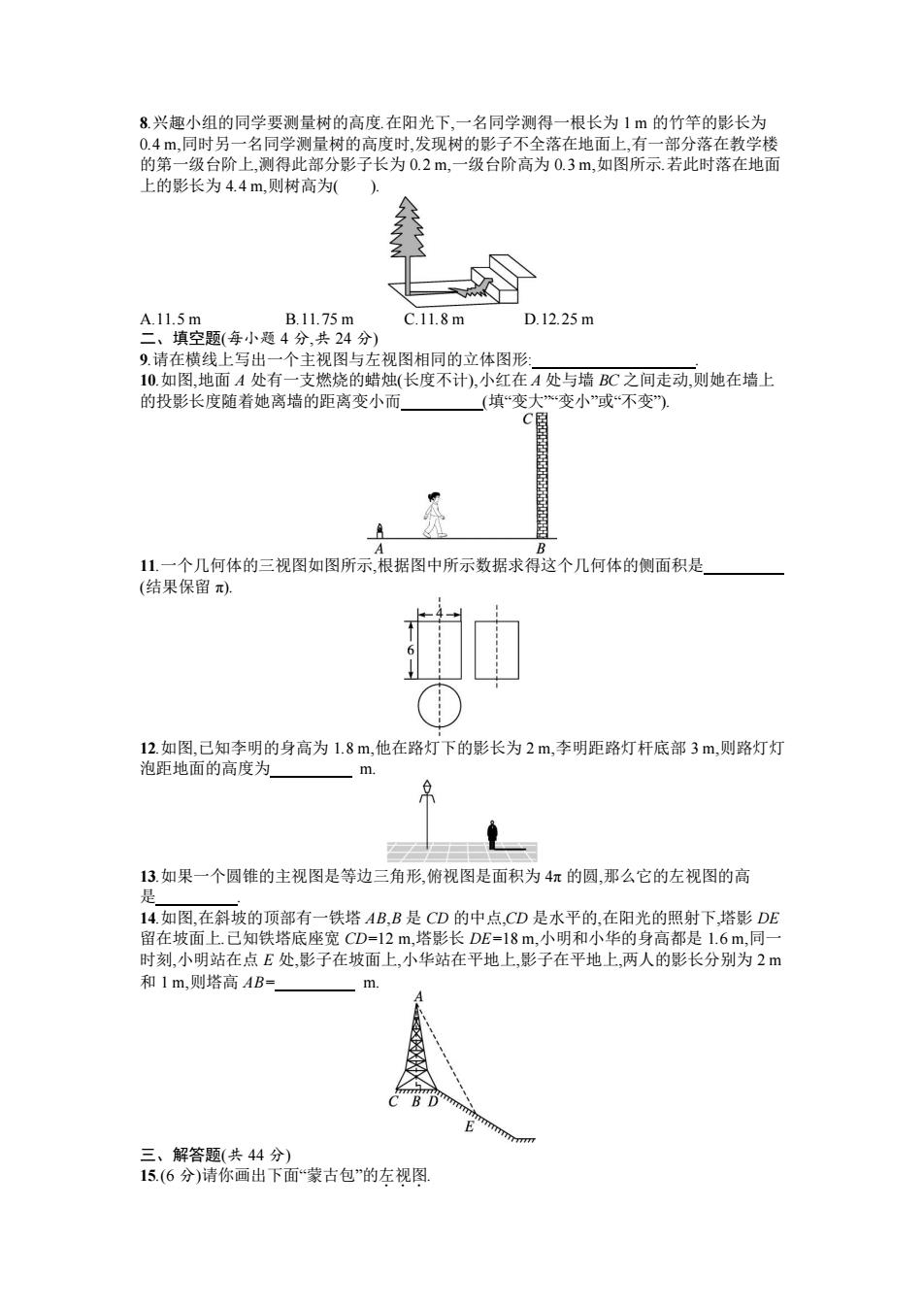
8.兴趣小组的同学要测量树的高度在阳光下,一名同学测得一根长为1的竹竿的影长为 0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼 的第一级台阶上,测得此部分影子长为0.2m,一级台阶高为0.3m,如图所示.若此时落在地面 上的影长为4.4m,则树高为(). A.11.5m B.11.75m C.11.8m D.12.25m 二、填空题(每小题4分,共24分) 9.请在横线上写出一个主视图与左视图相同的立体图形: 10.如图,地面A处有一支燃烧的蜡烛(长度不计),小红在A处与墙BC之间走动,则她在墙上 的投影长度随着她离墙的距离变小而 (填“变大*变小”或“不变). A B 11.一个几何体的三视图如图所示,根据图中所示数据求得这个几何体的侧面积是 (结果保留). 12.如图,已知李明的身高为1.8m,他在路灯下的影长为2m,李明距路灯杆底部3m,则路灯灯 泡距地面的高度为 m 13.如果一个圆锥的主视图是等边三角形,俯视图是面积为4π的圆,那么它的左视图的高 是 14.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE 留在坡面上.已知铁塔底座宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一 时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为2m 和1m,则塔高AB= m B D E 三、解答题(共44分) 15.(6分)请你画出下面“蒙古包”的左视图
8.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为 1 m 的竹竿的影长为 0.4 m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼 的第一级台阶上,测得此部分影子长为 0.2 m,一级台阶高为 0.3 m,如图所示.若此时落在地面 上的影长为 4.4 m,则树高为( ). A.11.5 m B.11.75 m C.11.8 m D.12.25 m 二、填空题(每小题 4 分,共 24 分) 9.请在横线上写出一个主视图与左视图相同的立体图形: . 10.如图,地面 A 处有一支燃烧的蜡烛(长度不计),小红在 A 处与墙 BC 之间走动,则她在墙上 的投影长度随着她离墙的距离变小而 (填“变大”“变小”或“不变”). 11.一个几何体的三视图如图所示,根据图中所示数据求得这个几何体的侧面积是 (结果保留 π). 12.如图,已知李明的身高为 1.8 m,他在路灯下的影长为 2 m,李明距路灯杆底部 3 m,则路灯灯 泡距地面的高度为 m. 13.如果一个圆锥的主视图是等边三角形,俯视图是面积为 4π 的圆,那么它的左视图的高 是 . 14.如图,在斜坡的顶部有一铁塔 AB,B 是 CD 的中点,CD 是水平的,在阳光的照射下,塔影 DE 留在坡面上.已知铁塔底座宽 CD=12 m,塔影长 DE=18 m,小明和小华的身高都是 1.6 m,同一 时刻,小明站在点 E 处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为 2 m 和 1 m,则塔高 AB= m. 三、解答题(共 44 分) 15.(6 分)请你画出下面“蒙古包”的左视图 ...
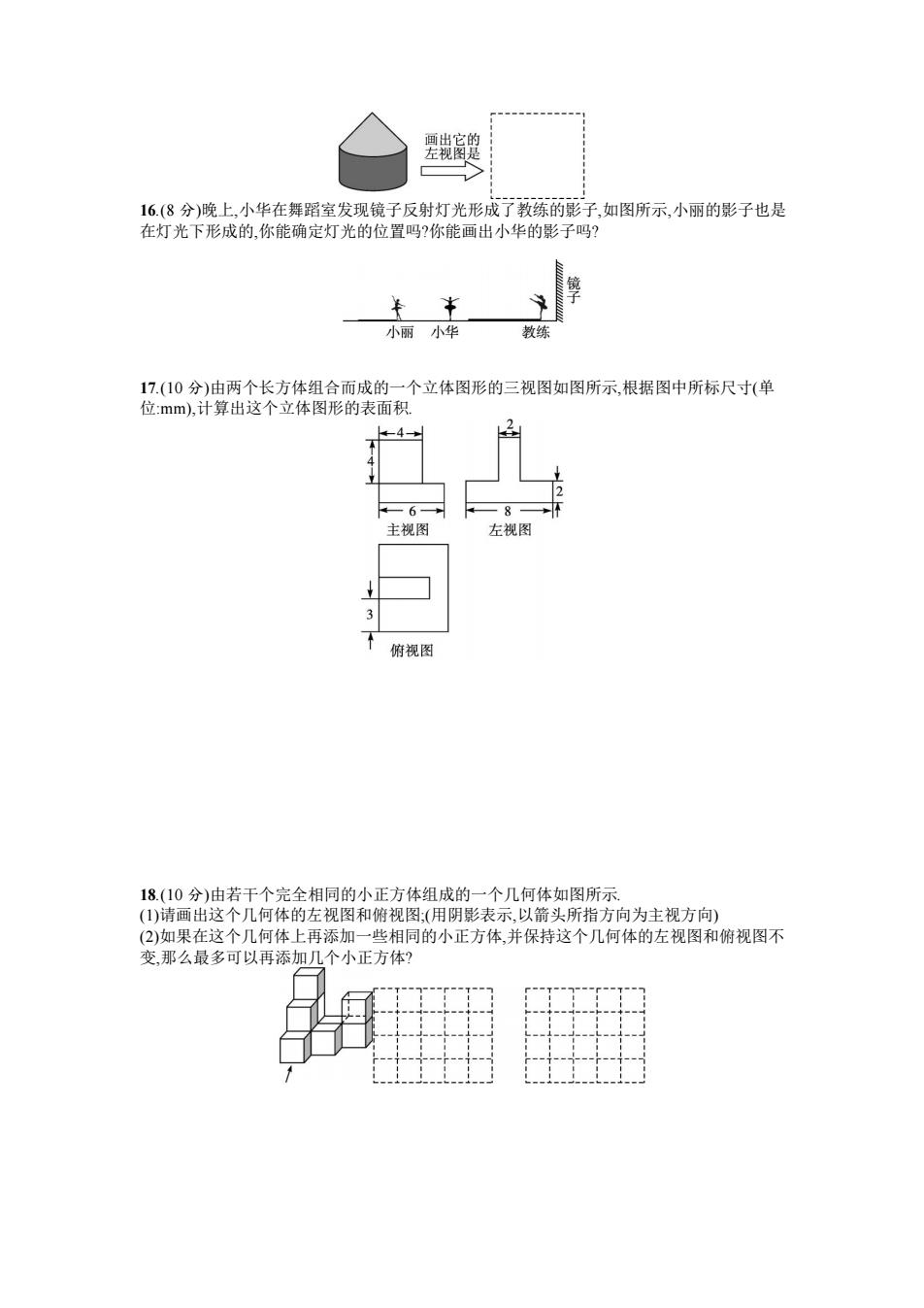
画出它的 左视图是 16.(8分)晚上,小华在舞蹈室发现镜子反射灯光形成了教练的影子,如图所示,小丽的影子也是 在灯光下形成的,你能确定灯光的位置吗?你能画出小华的影子吗? 子 小丽小华 教练 17.(10分)由两个长方体组合而成的一个立体图形的三视图如图所示,根据图中所标尺寸(单 位:mm),计算出这个立体图形的表面积 4 6- 主视图 左视图 3 俯视图 18.(10分)由若干个完全相同的小正方体组成的一个几何体如图所示 ()请画出这个几何体的左视图和俯视图:(用阴影表示,以箭头所指方向为主视方向) (2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不 变,那么最多可以再添加几个小正方体?
16.(8 分)晚上,小华在舞蹈室发现镜子反射灯光形成了教练的影子,如图所示,小丽的影子也是 在灯光下形成的,你能确定灯光的位置吗?你能画出小华的影子吗? 17.(10 分)由两个长方体组合而成的一个立体图形的三视图如图所示,根据图中所标尺寸(单 位:mm),计算出这个立体图形的表面积. 18.(10 分)由若干个完全相同的小正方体组成的一个几何体如图所示. (1)请画出这个几何体的左视图和俯视图;(用阴影表示,以箭头所指方向为主视方向) (2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不 变,那么最多可以再添加几个小正方体?

19.(10分)如图,在底面是正三角形的三棱柱中,边AB,A'B'垂直于投影面,且AB,A'B上的高所 在截面平行于投影面,若己知CD的投影长为2cm,CC的投影长为6cm. D D C (1)画出三棱柱在投影面P上的正投影, (2)求出三棱柱的表面积
19.(10 分)如图,在底面是正三角形的三棱柱中,边 AB,A'B'垂直于投影面,且 AB,A'B'上的高所 在截面平行于投影面,若已知 CD 的投影长为 2 cm,CC'的投影长为 6 cm. (1)画出三棱柱在投影面 P 上的正投影; (2)求出三棱柱的表面积
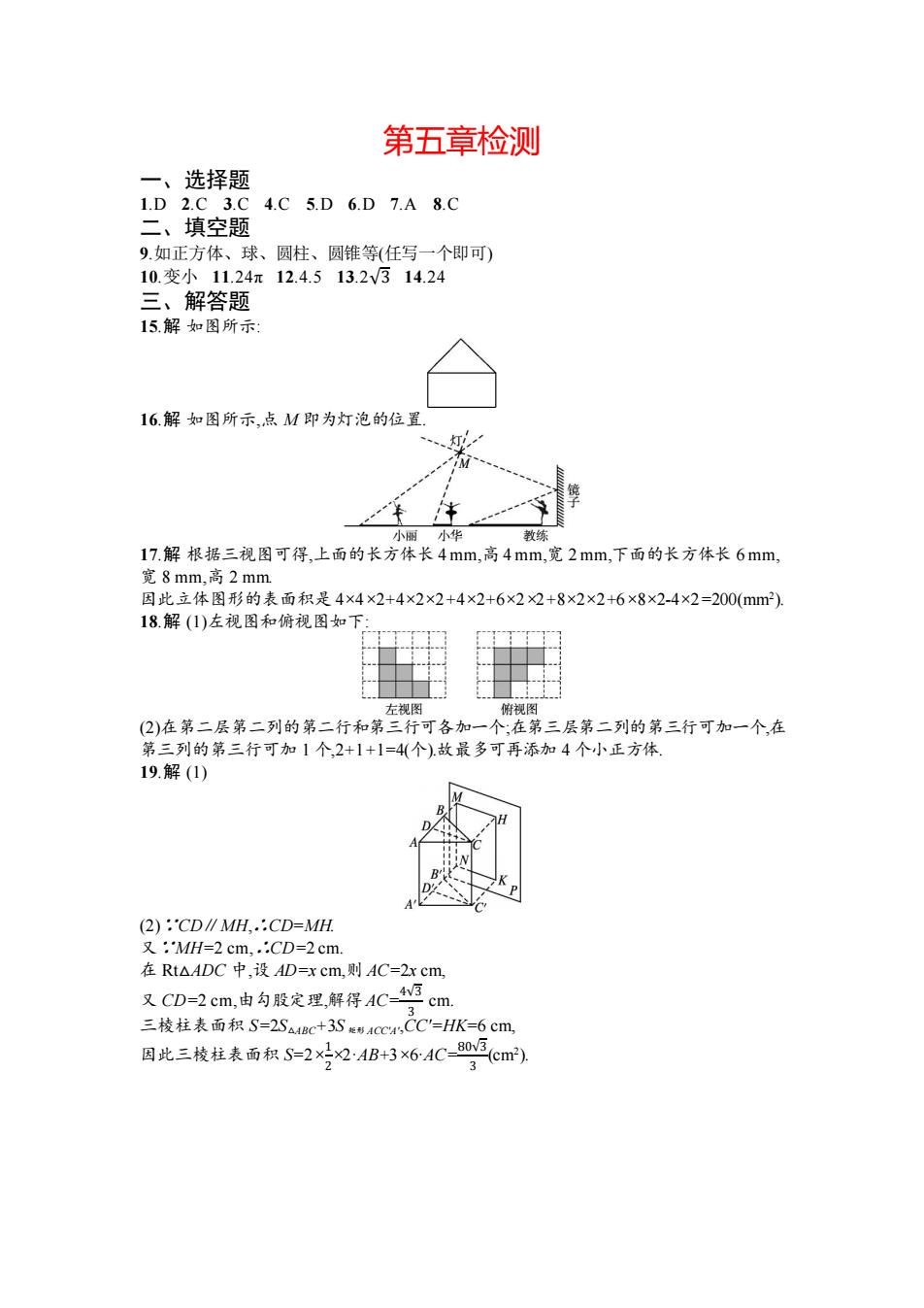
第五章检测 一、选择题 1.D2.C3.C4.C5.D6.D7.A8.C 二、填空题 9.如正方体、球、圆柱、圆锥等(任写一个即可) 10.变小11.24π12.4.513.2v314.24 三、解答题 15.解如图所示 16.解如图所示,点M即为灯泡的位置」 、灯 小丽小华 教练 17.解根据三视图可得,上面的长方体长4mm,高4mm,宽2mm,下面的长方体长6mm, 宽8mm,高2mm 因此立体图形的表面积是4×4×2+4×2×2+4×2+6×22+8×2×2+6×8×2-4×2=200(mm2). 18.解(1)左视图和俯视图如下 左视图 俯视图 (2)在第二层第二列的第二行和第三行可各加一个:在第三层第二列的第三行可加一个,在 第三列的第三行可加1个,2+1+1=4(个).故最多可再添加4个小正方体. 19.解(1) (2):CD∥MH,.:CD=MH 又:MH=2cm,.:CD=2cm. 在Rt△ADC中,设AD=xcm,则AC=2xcm, 又CD=2cm,由勾股定理,解得AC-4 3 cm. 三棱柱表面积S=2SaM4Bc+3S形4CC4CC'=HK=6Cm 因此三棱柱表面积S=2x24B3×64C-0cm)
第五章检测 一、选择题 1.D 2.C 3.C 4.C 5.D 6.D 7.A 8.C 二、填空题 9.如正方体、球、圆柱、圆锥等(任写一个即可) 10.变小 11.24π 12.4.5 13.2√3 14.24 三、解答题 15.解 如图所示: 16.解 如图所示,点 M 即为灯泡的位置. 17.解 根据三视图可得,上面的长方体长 4 mm,高 4 mm,宽 2 mm,下面的长方体长 6 mm, 宽 8 mm,高 2 mm. 因此立体图形的表面积是 4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2 ). 18.解 (1)左视图和俯视图如下: (2)在第二层第二列的第二行和第三行可各加一个;在第三层第二列的第三行可加一个,在 第三列的第三行可加 1 个,2+1+1=4(个).故最多可再添加 4 个小正方体. 19.解 (1) (2)∵CD∥MH,∴CD=MH. 又∵MH=2 cm,∴CD=2 cm. 在 Rt△ADC 中,设 AD=x cm,则 AC=2x cm, 又 CD=2 cm,由勾股定理,解得 AC=4√3 3 cm. 三棱柱表面积 S=2S△ABC+3S 矩形 ACC'A',CC'=HK=6 cm, 因此三棱柱表面积 S=2× 1 2 ×2·AB+3×6·AC=80√3 3 (cm2 )