
第九章统计热力学初步 学习要求 1.明确统计热力学系统的有关概念 2.理解能级、能级的简并度和能级分布的意义 3.理解并掌握玻尔茨曼分布的意义和应用 4.掌握配分函数的意义及计算 5.理解并掌握配分函数和热力学状态函的关系 主要公式及其适用条件 1.分子能级为各种独立运动能级之和 6=十6十十6e十6n 2.粒子各运动形式的能级及能级的简并度 (1)三维平动子 4+ (nx,my,nz=1,2…) 简并度:当4=6=c时有简并(产:+:+m)相等的能级为简 并的。 (2)刚性转子 (双原子分子): 0+W0=012) 其中 = 1+m2, 简并度为:g=2J+1。 (3)一维谐振子
第九章 统计热力学初步 学习要求 1. 明确统计热力学系统的有关概念 2. 理解能级、能级的简并度和能级分布的意义 3. 理解并掌握玻尔茨曼分布的意义和应用 4. 掌握配分函数的意义及计算 5. 理解并掌握配分函数和热力学状态函的关系 主要公式及其适用条件 1. 分子能级为各种独立运动能级之和 2. 粒子各运动形式的能级及能级的简并度 (1)三维平动子 简并度:当 a = b = c 时有简并,( )相等的能级为简 并的。 (2)刚性转子 (双原子分子): 其中 。 简并度为:gr,J = 2J + 1。 (3)一维谐振子
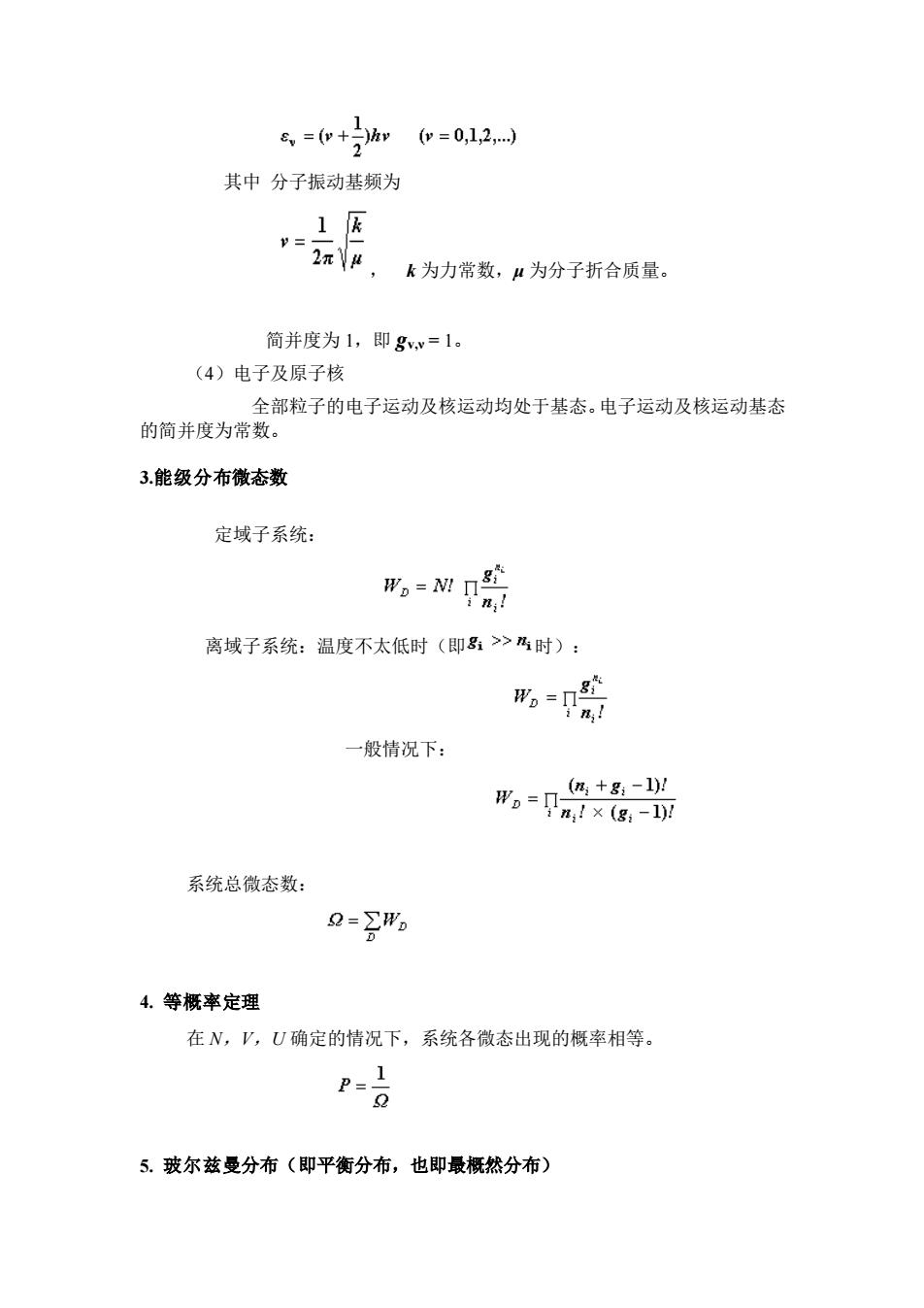
8=o+hwu=012 其中分子振动基频为 1k -7H 。k为力常数,μ为分子折合质量。 简并度为1,即g,v=1。 (4)电子及原子核 全部粒子的电子运动及核运动均处于基态。电子运动及核运动基态 的简并度为常数。 3.能级分布微态数 定域子系统: 那=”畸 离域子系统:温度不太低时(即>时): %哈 一般情况下: (%+g-1/ 形。=a1×(8,-可 系统总微态数: 9=2形, 4.等概率定理 在N,V,U确定的情况下,系统各微态出现的概率相等。 5.玻尔兹曼分布(即平衡分布,也即最概然分布)
其中 分子振动基频为 , k 为力常数,μ 为分子折合质量。 简并度为 1,即 gv,ν = 1。 (4)电子及原子核 全部粒子的电子运动及核运动均处于基态。电子运动及核运动基态 的简并度为常数。 3.能级分布微态数 定域子系统: 离域子系统:温度不太低时(即 时): 一般情况下: 系统总微态数: 4. 等概率定理 在 N,V,U 确定的情况下,系统各微态出现的概率相等。 5. 玻尔兹曼分布(即平衡分布,也即最概然分布)

Stirling公式: In N!=NInN-N 粒子的配分函数: 玻尔兹曼分布: n=N 9 品e专 能级i的有效容量: 多,e当r 6.配分函数的析因子性质 9=:乐4,9。乐 7.能量零点的选择对配分函数的影响 若基态能级能量值为品,以基态为能量零点时,能量值金=气一 9=2,eM ”8ae=e知 g 即g.e 常温下,平动及转动配分函数与能量零点选择几乎无关,但振动配分函数 与能量零点选择有关。即: g公g;:6=7r=e网27104 电子运动与核运动的配分函数,与能量零点选择也有关。 无关 有关 与能量零点 S.Cv. U,H,A,G 与定域或离域 U,H S,A,G
Stirling 公式: 粒子的配分函数: 玻尔兹曼分布: 能级 i 的有效容量: 6. 配分函数的析因子性质 7. 能量零点的选择对配分函数的影响 若基态能级能量值为 ,以基态为能量零点时,能量值 常温下,平动及转动配分函数与能量零点选择几乎无关,但振动配分函数 与能量零点选择有关。即: 电子运动与核运动的配分函数,与能量零点选择也有关。 无关 有关 与能量零点 U,H,A,G 与定域或离域 U,H S,A,G

8配分函数的计算 平动: -2arv 转动(对线性刚性转子): 27 若设 2 8,21k,则当T>0:时, 其中。为绕通过质心,垂直于分子的轴旋转一周出现的不可分辨的几何位 置的次数,即分子对称数。对线性刚性转子转动自由度为2。 振动: =2em叶rew三.em灯] ¥-。 若设 x=eo ,当T<Q时(常温),振动 运动量子化效应突出,不能用积分代替加和: %。空。。0, 1-x 1 4=1-x 电子运动:因为电子运动全部处于基态,电子运动能级完全没有开放,求 和项中自第二项起均可被忽略。所以: 久.=oe5灯;=8o=const
8.配分函数的计算 平动: 转动(对线性刚性转子): 其中 若设 ,则当 T >> Qr 时, , 其中 σ 为绕通过质心,垂直于分子的轴旋转一周出现的不可分辨的几何位 置的次数,即分子对称数。对线性刚性转子转动自由度为 2。 振动: 若设 ,当 T<<Qv 时(常温),振动 运动量子化效应突出,不能用积分代替加和: 电子运动: 因为电子运动全部处于基态,电子运动能级完全没有开放,求 和项中自第二项起均可被忽略。所以:

核运动: 4=0e气0r;g=g0=.const 9.热力学能与配分函数的关系 此处U可代表: (1)总热力学能: (2)零点为co时的热力学能(U0=U-Neo); (3)平动能:表示相应的配分函数。 (4)当U代表:转动能,振动能,电子能,核能时,9与V无关, 偏微商可写作全微商。 Uh与U°关系:只有 4受, us欧;U=;U。=;U=。 10.摩尔定容热容与配分函数关系 “9=g”g6%7 0与T无关。所以,Cm与零点能选择无关。 c-(0-r(]小-r等} Cvm Cvt+Cvr +Cvv 11.玻尔兹曼熵定理 S=kIn2
核运动: 9. 热力学能与配分函数的关系 此处 Ui 可代表: (1)总热力学能; (2)零点为 e0 时的热力学能(U0 = U - Nε0); (3)平动能;qi 表示相应的配分函数。 (4)当 Ui 代表:转动能,振动能,电子能,核能时,qi 与 V 无关, 偏微商可写作全微商。 Ui 与 Ui 0 关系:只有 ,其余: 。 10. 摩尔定容热容与配分函数关系 ,ε0 与 T 无关。所以,Cv,m与零点能选择无关。 11. 玻尔兹曼熵定理

摘取最大项原理:若最概然分布微态数为W,总微态数为2,当N无限 特6资 ,所以可用lnw代替nQ。这种近似方法称为摘取最大项 原理。 12.熵与配分函数关系 离域子系统: S=是+号+ (嫡与零点能的选择无关) 定域子系统: S=N灿4+7 由于,配分函数的析因子性质,及 r=r++++ 有:5=8+9+父+.+ 对离域子系统,各独立运动的熵可表示为: &=灿等+号a &=M+ T (i=r,v,e;n) 13.统计熵的计算 般物理化学过程,只涉及S,S,S (N为阿佛加得罗常数) &m S,=-Rnl1-小+T- RO,x 其中c=eI
摘取最大项原理:若最概然分布微态数为 WB,总微态数为 Ω,当 N 无限 增大时, , 所以可用 lnWB 代替 lnΩ 。这种近似方法称为摘取最大项 原理。 12. 熵与配分函数关系 离域子系统: (熵与零点能的选择无关) 定域子系统: 由于,配分函数的析因子性质,及 有: 对离域子系统,各独立运动的熵可表示为: 13. 统计熵的计算 一般物理化学过程,只涉及 St ,Sr ,Sv (N0 为阿佛加得罗常数)

14.其它热力学函数与配分函数的关系 A=-kTInQ 离域子: 定域子: Q=q A=-kTIng" 其它G,H可由热力学关系导出。 =4-:=0-, 15.理想气体的标准摩尔吉布斯函数 G,--RT--RThum 16.理想气体的标准摩尔吉布斯自由能函数 6,m T 17.理想气体的标准摩尔格函数 (h ta).ar) 思考题 1.什么是独立子系统?什么是近独立子系统?什么是相依子系统? 2.平动、转动、振动能级间隔大约是多少? 3.为什么最概然分布是平衡分布? 4.能量零点的不同选择是否会影响能级分布数
14. 其它热力学函数与配分函数的关系 离域子: , 定域子: , 其它 G,H 可由热力学关系导出。 15. 理想气体的标准摩尔吉布斯函数 16. 理想气体的标准摩尔吉布斯自由能函数 17. 理想气体的标准摩尔焓函数 思考题 1. 什么是独立子系统? 什么是近独立子系统? 什么是相依子系统? 2. 平动、转动、振动能级间隔大约是多少? 3. 为什么最概然分布是平衡分布? 4. 能量零点的不同选择是否会影响能级分布数

5.沟通化学热力学与统计热力学的重要公式是什么? 6.从统计热力学上证明理想气体的热力学能只是温度的函数。 7.为什么双原子理想气体分子的C,有R或乙R的值? 8.为什么有些物质的统计熵和量热熵有一定的差别? 9.选择不同的能量零点对配分数函数和热力学函数的影响是怎样的? 10.有三个一维谐振子,振动能£,≥6,的粒子数所占的百分数是多少?(j为振 动量子数)
5. 沟通化学热力学与统计热力学的重要公式是什么? 6. 从统计热力学上证明理想气体的热力学能只是温度的函数。 7. 为什么双原子理想气体分子的 Cv,m 有 R 2 5 或 R 2 7 的值? 8. 为什么有些物质的统计熵和量热熵有一定的差别? 9. 选择不同的能量零点对配分数函数和热力学函数的影响是怎样的? 10. 有三个一维谐振子, 振动能 v j 的粒子数所占的百分数是多少? ( j 为振 动量子数)