
试卷代号:1318 座位号■1 国家开放大学(中央广播电视大学)2016年春季学期“开放本科”期末考试 社会统计学试题(半开卷) 2016年7月 题 号 二 三 四 总分 分 数 得 分 评卷人 一、单项选择题(每题只有一个正确答案,请将正确答案的字母填写 在括号内。每题2分,共20分)》 1.为了解某地区的消费,从该地区随机抽取8000户进行调查,其中80%回答他们的月消费 在3000元以上,20%回答他们每月用于通讯、网络的费用在300元以上,此处8000户是()。 A.样本 B.总体 C.变量 D.统计量 2.某地区家庭年均收人可以分为以下六组:1)1500元及以下;2)1500-2500元:3)2500 3500元;4)3500一4500元;5)4500-5500元;6)5500元及以上,则该分组的组距近似为()。 A.500元 B.1500元 C.1250元 D.1000元 3.先将总体按某标志分为不同的类别或层次,然后在各个类别中采用简单随机抽样或系统 抽样的方式抽取子样本,最后将所有子样本合起来作为总样本,这样的抽样方式称为()。 A.简单随机抽样 B.系统抽样 C.整群抽样 D.分层抽样 4.正态分布中,。值越小,则()。 A.离散趋势越小 B.离散趋势越大 C.曲线越低平 D.变量值越分散 5.对于左偏分布,平均数、中位数和众数之间的关系是()。 A.平均数>中位数>众数 B.中位数>平均数>众数 C.众数>中位数>平均数 D.众数>平均数>中位数 1143
试卷代号 :1318 座位号 国家开放大学(中央广播电视大学 )2016 年春季学期"开放本科"期末考试 社会统计学试题(半开卷) 2016 E 四四 一、单项选择题{每题只有一个正确答案,请将正确答案的字母填写 在括号内。每题 分,共 20 分} 1.为了解某地区的消费.从该地区随机抽取 8000 户进行调查,其中 80% 回答他们的月消费 3000 元以上, 20% 回答他们每月用于通讯、网络的费用在 300 元以上,此处 8000 户是( )。 A. 样本 B. 总体 C. 变量 D. 统计量 2. 某地区家庭年均收人可以分为以下六组: 1) 1500 元及以下 ;2)1500-2500 JG;3)2500- 3500 ;4)3500-4500 ;5 )4500 5500 ;6)5500 元及以上,则该分组的组距近似为( )。 A. 500 C. 1250 B. 1500 D. 1000 3. 先将总体按某标志分为不同的类别或层次,然后在各个类别中采用简单随机抽样或系统 抽样的方式抽取子样本,最后将所有子样本合起来作为总样本,这样的抽样方式称为( )。 A. 简单随机抽样 C. 整群抽样 4. 正态分布中, 值越小,则( )。 A. 离散趋势越小 C. 曲线越低平 B.系统抽样 D. 分层抽样 B. 离散趋势越大 D. 变量值越分散 5. 对于左偏分布,平均数、中位数和众数之间的关系是( )。 A. 平均数〉中位数〉众数 B. 中位数〉平均数〉众数 C. 众数〉中位数〉平均数 D. 众数〉平均数〉中位数 1143

6.有甲、乙两人同时打靶,各打10靶,甲平均每靶为8环,标准差为2;乙平均每靶9环, 标准差为3,以下甲、乙两人打靶的稳定性水平表述正确的是()。 A.甲的离散程度小,稳定性水平低 B.甲的离散程度小,稳定性水平高 C.乙的离散程度小,稳定性水平低 D.乙的离散程度大,稳定性水平高 7.下表是某单位工作人员年龄分布表,该单位工作人员的平均年龄是()。 组别 按年龄分组(岁) 工作人员数(人) 1 20~24 6 2 2529 14 3 30~34 24 4 35~39 18 5 40~44 12 6 45~49 18 7 5054 14 8 5559 6 合计 112 A.37 B.35 C.36 D.39 8.某单位对该厂第一加工车间残品率估计高于13%,而该车间主任认为该比例偏高,如 果要检验该说法是否正确,则假设形式应该为()。 A.H。:π≥0.13;H1:π0.13 C.H。:x=0.13;H1:π≠0.13 D.H:r>0.13;H1:π≤0.13 9.残差平方和(SSE)反映了y的总变差中(). A.由于x与y之间的线性关系引起的y的变化部分 B.x对y的现有影响之外,其他因素对y变差的影响 C.由于x与y之间的非线性关系引起的y的变化部分 D.由于x与y之间的函数关系引起的y的变化部分 10.从两个总体中共选取了8个观察值,得到组间平方和为432,组内平方和为426,则组 间均方和组内均方分别为()。 A.432,71 B.216,71 C.432,426 D.216,426 1144
6. 有甲、乙两人同时打靶,各打 10 靶,甲平均每靶为 环,标准差为 2; 乙平均每靶 环, 标准差为 ,以下甲、乙两人打靶的稳定性水平表述正确的是( )。 A. 甲的离散程度小,稳定性水平低 B. 甲的离散程度小,稳定性水平高 c.乙的离散程度小,稳定性水平低 D. 乙的离散程度大,稳定性水平高 7. 下表是某单位工作人员年龄分布表,该单位工作人员的平均年龄是( )。 A. 37 C. 36 组别 1 2 3 4 5 6 7 8 按年龄分组(岁〉 20~24 25~29 30~34 35~39 40~44 45~49 50~54 55~59 合计 B. 35 D. 39 工作人员数(人〉 6 14 24 18 12 18 14 6 112 8. 某单位对该厂第一加工车间残品率估计高于 13% ,而该车间主任认为该比例偏高,如 果要检验该说法是否正确,则假设形式应该为( )。 A. Ho:π 0.13; :π0. 13 D. Ho:π>0.13;H :π~0.13 9. 残差平方和 (SSE) 反映了 的总变差中( )。 A. 由于 之间的线性关系引起的 的变化部分 B. 的现有影响之外,其他因素对 变差的影响 c.由于 之间的非线性关系引起的 的变化部分 D. 由于 之间的函数关系引起的 的变化部分 10. 从两个总体中共选取了 个观察值,得到组间平方和为 432 ,组内平方和为 426 ,则组 间均方和组内均方分别为( )。 1144 A. 432 ,71 C. 432 ,426 B. 216 ,71 D. 216 ,426
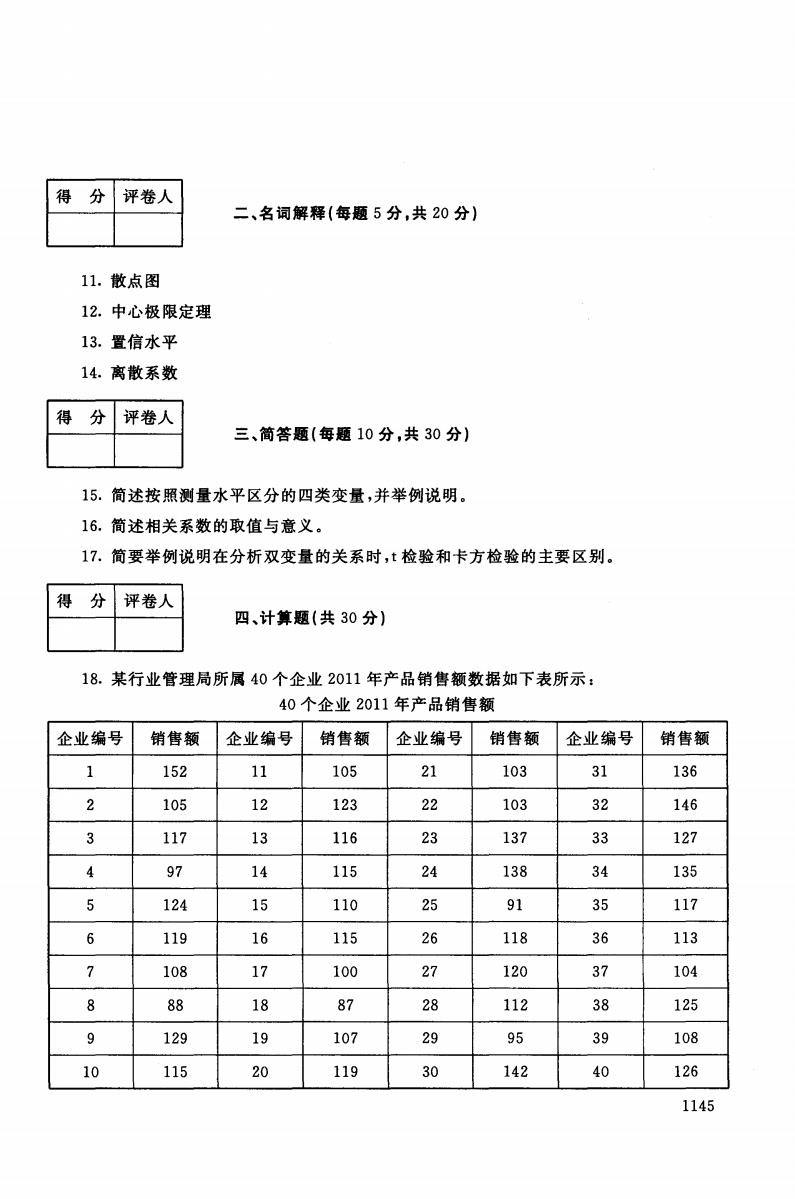
得分 评卷人 二、名词解释(每题5分,共20分) 11.散点图 12.中心极限定理 13.置信水平 14.离散系数 得 分 评卷人 三、简答题(每题10分,共30分) 15.简述按照测量水平区分的四类变量,并举例说明。 16.简述相关系数的取值与意义。 17.简要举例说明在分析双变量的关系时,t检验和卡方检验的主要区别。 得 分 评卷人 四、计算题(共30分)】 18.某行业管理局所属40个企业2011年产品销售额数据如下表所示: 40个企业2011年产品销售额 企业编号 销售额 企业编号 销售额 企业编号 销售额 企业编号 销售额 1 152 11 105 21 103 31 136 2 105 12 123 22 103 32 146 3 117 13 116 23 137 33 127 4 97 14 115 24 138 34 135 5 124 15 110 25 91 35 117 6 119 16 115 26 118 36 113 2 108 17 100 27 120 37 104 8 88 18 87 28 112 38 125 9 129 19 107 29 95 39 108 10 115 20 119 30 142 40 126 1145
|得分|评卷人| | 1.散点图 12. 中心极限定理 13. 置信水平 14. 离散系数 |得分|评卷人| | 二、名词解释{每题 分,共 20 分} 三、简答题{每题 10 分,共 30 分} 15. 简述按照测量水平区分的四类变量,并举例说明。 16. 简述相关系数的取值与意义。 17. 简要举例说明在分析双变量的关系时, 检验和卡方检验的主要区别。 |得分|评卷人| | 四、计算题{共 30 分} 18. 某行业管理局所属 40 个企业 2011 年产品销售额数据如下表所示= 40 个企业 2011 年产品销售额 企业编号 销售额 企业编号 销售额 企业编号 销售额 企业编号 1 152 11 105 21 103 31 2 105 12 123 22 103 32 3 117 13 116 23 137 33 4 97 14 115 24 138 34 5 124 15 110 25 91 35 6 119 16 115 26 118 36 7 108 17 100 27 120 37 8 88 18 87 28 112 38 9 129 19 107 29 95 39 10 115 20 119 30 142 40 销售额 136 146 127 135 117 113 104 125 108 126 1145

要求: (1)对2011年40个企业销售额按由低到高进行排序,求出众数、中位数和平均数。 (2)如果按照规定,销售额在125万元以上的为先进企业,115万一125万之间的为良好企 业,105万一115万之间的为一般企业,105万以下的为落后企业,请按先进企业、良好企业、一 般企业、落后企业进行分组,编制频数分布表,并计算累积频数和累积频率。 19.某汽车生产商欲了解广告费用(万元)对销售量(辆)的影响。收集了过去12年的有 关数据,通过分析得到:方程的截距为363,回归系数为1.42,回归平方和SSR=1600,残差平 方和SSE=450。 要求: (1)写出销售量y与广告费用x之间的线性回归方程。 (2)假如明年计划投人广告费用为50万,根据回归方程估计明年汽车销售量。 (3)计算判定系数R2,并解释它的意义。 1146
要求: (1)对 2011 40 个企业销售额按由低到高进行排序,求出众数、中位数和平均数。 (2) 如果按照规定,销售额在 125 万元以上的为先进企业, 115 -125 万之间的为良好企 业, 105 万一 115 万之间的为一般企业, 105 万以下的为落后企业,请按先进企业、良好企业、一 般企业、落后企业进行分组,编制频数分布表,并计算累积频数和累积频率。 190 某汽车生产商欲了解广告费用(万元)对销售量(辆〉的影响。收集了过去 12 年的有 关数据,通过分析得到 方程的截距为 363 ,回归系数为1. 42 ,回归平方和 SSR=1600 ,残差平 方和 SSE=450. 要求 (1)写出销售量 与广告费用 之间的线性回归方程. (2) 假如明年计划投入广告费用为 50 万,根据回归方程估计明年汽车销售量。 (3) 计算判定系数 ,并解释它的意义。 1146

试卷代号:1318 国家开放大学(中央广播电视大学)2016年春季学期“开放本科”期末考试 社会统计学试题答案及评分标准(半开卷) (供参考) 2016年7月 一、单项选择题(每题2分,共20分) 1.A 2.D 3.D 4.A 5.A 6.B 7.D 8.A 9.B 10.A 二、名词解释(每题5分,共20分) 11.散点图:在坐标系中,用X轴表示自变量x,用Y轴表示因变量y,而变量组(x,y)则 用坐标系中的点表示,不同的变量组在坐标系中形成不同的散点,用坐标系及其坐标系中的散 点形成的二维图就是散点图。(5分) 12.中心极限定理:中心极限定理具体内容为:不论总体分布是否服从正态分布,从均值 为4、方差为c2的总体中,抽取容量为n的随机样本,当n充分大时(通常要求n≥30),样本均 值的抽样分布近似服从均值为μ、方差为c2/n的正态分布。(5分) 13.置信水平:置信水平就是将构造置信区间的步骤重复很多次,置信区间包含总体参数 真值的次数所占的比例。(5分) 14.离散系数:离散系数是一组数据的标准差与该数据均值之比,也称为变异系数。 (5分) 三、简答题(每题10分,共30分) 15.简述按照测量水平区分的四类变量,并举例说明。 (1)定类变量:当变量值的含义仅表示个体的不同类别,而不能说明个体的大小、程度等其 它特征时,这种变量称为定类变量。(2分)例如:性别。(0.5分) (2)定序变量:当变量值的含义不仅表示个体的不同类别,还可以区分个体之间大小、程度 等序次差异时,这种变量称为定序变量。(2分)例如:学历。(0.5分) 1147
试卷代号 :1318 国家开放大学(中央广播电视大学 )2016 年春季学期"开放本科"期末考试 社会统计学 试题答案及评分标准(半开卷) 一、单项选择题{每题 分,共 20 分} 1. A 6. B 2. D 7. D 二、名词解释{每题 分,共 20 分) (供参考) 3.D 8.A 4.A 9. B 5.A 10. A 2016 1.散点图 在坐标系中,用 轴表示自变量 ,用 轴表示因变量 ,而变量组 (x y) 用坐标系中的点表示,不同的变量组在坐标系中形成不同的散点,用坐标系及其坐标系中的散 点形成的二维图就是散点图。 (5 分〉 12. 中心极限定理 中心极限定理具体内容为:不论总体分布是否服从正态分布,从均值 、方差为 σ2 的总体中,抽取容量为 的随机样本,当 充分大时(通常要求 二三30) ,样本均 值的抽样分布近似服从均值为 、方差为 σ2/n 的正态分布。 (5 分〉 13. 置信水平 置信水平就是将构造置信区间的步骤重复很多次,置信区间包含总体参数 真值的次数所占的比例。 (5 分〉 14. 离散系数:离散系数是一组数据的标准差与该数据均值之比,也称为变异系数。 (5 分) 三、简答题{每题 10 分,共 30 分} 15. 简述按照测量水平区分的四类变量,并举例说明。 (1)定类变量 当变量值的含义仅表示个体的不同类别,而不能说明个体的大小、程度等其 它特征时,这种变量称为定类变量。 (2 分〉例如:性别。 (0. 分) (2) 定序变量 当变量值的含义不仅表示个体的不同类别,还可以区分个体之间大小、程度 等序次差异时,这种变量称为定序变量。 (2 分)例如:学历。 (0.5 分) 1147

(3)定距变量:当变量值不仅可以将个体区分为不同类型并进行排序,而且可以确定不同 类别之间的数量差别和间隔差距时,这样的变量称为定距变量。(2分)例如:智商。(0.5分) (4)定比变量:除了上述三种变量的全部特征外,还可以计算两个变量值之间的比值时,这 样的变量称为定比变量。(2分)例如:收入。(0.5分) 16.简述相关系数的取值与意义。 相关系数的取值在一1~1之间;(2分)相关系数的正负号表示两个变量相关关系的方向, “+”表示正相关,“一”表示负相关;(2分)相关系数的绝对值表示相关关系的程度,绝对值越 大,相关程度越大,即r越接近1;(2分)反之,绝对值越小,及r越接近0,相关程度越弱:(2 分)相关系数r=0时,只能说变量之间不存在线性相关,而不能说它们之间不相关(2分)。 17.简要举例说明在分析双变量的关系时,t检验和卡方检验的主要区别。 分析双变量关系时,t检验和卡方检验都是主要用于检验这两个变量之间是否存在显著 关系。(2分)t检验主要用于对一个为数值型变量、另一个为分类变量且只有两个类别的变量 的双变量关系的统计显著性检验。(2分)卡方检验主要用于对两个分类变量之间的相关性进 行统计检验,判断变量之间是否存在显著关系。(2分) 例如,我们想考察收人与性别是否存在关系,或者两性的收入是否存在显著差异,可以用 两独立样本t检验。(2分)如果我们想考察职业与性别是否存在关系,而职业和性别都是分 类变量,那么可以用卡方检验考察不同性别之间职业是否存在显著差异。(2分) 四、计算题(共30分) 18.(1)销售额由低到高排序:(5分) 87、88、91、95、97、100、103、103、104、105、105、107、108、108、110、112、113、115、115、115、 116、117、117、118、119、119、120、123、124、125、126、127、129、135、136、137、138、142、146、 152 众数:115(1分) 中位数:115.5(1分) 平均数:X=X十Xa十…十XN N =(152+146+…+88+87)÷40 =4647÷40 =116.175(3分) 1148
(3) 定距变量 当变量值不仅可以将个体区分为不同类型并进行排序,而且可以确定不同 类别之间的数量差别和间隔差距时,这样的变量称为定距变量。 (2 分)例如 智商。 (0.5 分〉 (4) 定比变量 除了上述三种变量的全部特征外,还可以计算两个变量值之间的比值时,这 样的变量称为定比变量 (2 分)例如:收人。 (0.5 分〉 16. 简述相关系数的取值与意义。 相关系数的取值在一 1-1 之间 ;(2 分)相关系数的正负号表示两个变量相关关系的方向, "+"表示正相关"一"表示负相关 ;(2 分)相关系数的绝对值表示相关关系的程度,绝对值越 大,相关程度越大,即 越接近 1;(2 分〉反之,绝对值越小,及 越接近 ,相关程度越弱 ;(2 分〉相关系数 r=O 时,只能说变量之间不存在线性相关,而不能说它们之间不相关 (2 分)。 17. 简要举例说明在分析双变量的关系时, 检验和卡方检验的主要区别。 分析双变量关系时, 检验和卡方检验都是主要用于检验这两个变量之间是否存在显著 关系。 (2 分)t检验主要用于对一个为数值型变量、另一个为分类变量且只有两个类别的变量 的双变量关系的统计显著性检验。 (2 分)卡方检验主要用于对两个分类变量之间的相关性进 行统计检验,判断变量之间是否存在显著关系。 (2 分) 例如,我们想考察收入与性别是否存在关系,或者两性的收入是否存在显著差异,可以用 两独立样本 检验。 (2 分〉如果我们想考察职业与性别是否存在关系,而职业和性别都是分 类变量,那么可以用卡方检验考察不同性别之间职业是否存在显著差异。 (2 分) 四、计算题{共 30 分) 18. (1)销售额由低到高排序 :(5 分) 87 88 91 95 97 100 103 103 104 105 105 107 108 108 110 112 113 115 115 115 116 117 117 118 119 119 120 123 124 125 126 127 129 135 136 137 138 142 146 152 众数 :115 (1分〉 中位数 :115.5 (1分) X 1 +X2 + … +X N 平均数 X=--"--O =(152+146+……+88+87) -7- 40 =4647 -7- 40 =116.175 (3 分〉 1148
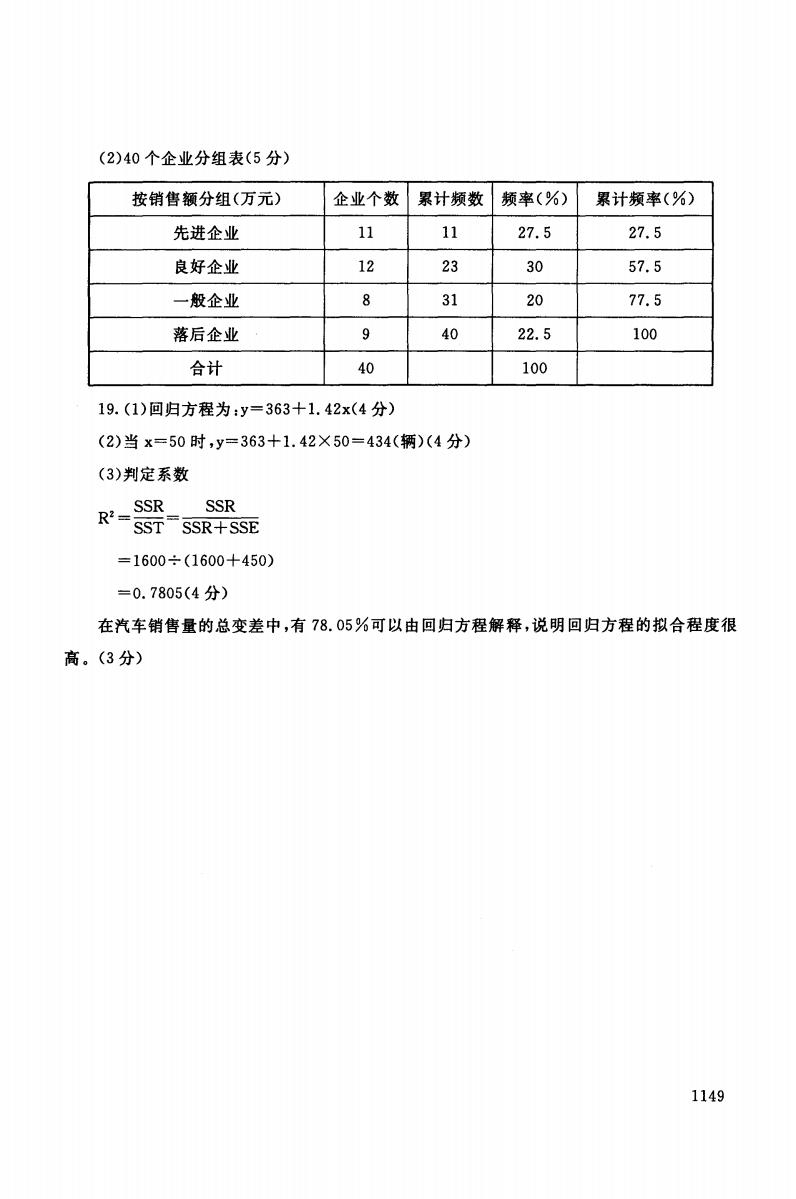
(2)40个企业分组表(5分) 按销售额分组(万元) 企业个数 累计频数 频率(%) 累计频率(%) 先进企业 11 11 27.5 27.5 良好企业 12 23 30 57.5 一般企业 8 31 20 77.5 落后企业 9 40 22.5 100 合计 40 100 19.(1)回归方程为:y=363+1.42x(4分) (2)当x=50时,y=363+1.42×50=434(辆)(4分) (3)判定系数 R:=SSR SSR SST SSR+SSE =1600÷(1600+450) =0.7805(4分) 在汽车销售量的总变差中,有78.05%可以由回归方程解释,说明回归方程的拟合程度很 高。(3分) 1149
(2)40 个企业分组表 (5 分〉 按销售额分组(万元〉 企业个数 累计频数 先进企业 11 11 良好企业 12 23 一般企业 8 31 落后企业 9 40 合计 40 19. (1)回归方程为 :y=363+ l. 42x(4 分〉 (2) x=50 时, y=363+ 1. 42X 50=434( )(4 分) (3) 判定系数 RZ=EEEZSSR SST SSR+SSE = 1600+ (1 600+450) =0.7805(4 分〉 频率(%) 累计频率(%) 27.5 27.5 30 57.5 20 77.5 22.5 100 100 在汽车销售量的总变差中,有 78.05% 可以由回归方程解释,说明回归方程的拟合程度很 高。 (3 分〉 1149