
一海大理学院表学裸件 大学物理学电子教索 气体动理论(2) 7-4能量均分定理理想气体内能 7-5麦克斯韦气体速率分布律 7-6玻尔滋曼能量分布律等温气压公
大学物理学电子教案 海大理学院教学课件 气体动理论(2) 7-4 能量均分定理 理想气体内能 7-5 麦克斯韦气体速率分布律 7-6 玻尔兹曼能量分布律 等温气压公式

复习 气体动理论的基本观点 理想气体的微观模型 理想气体压强公式 p=号(m)=号 理想气体的温度 2 3 my kT 2 2
复 习 •气体动理论的基本观点 •理想气体的微观模型 •理想气体压强公式 n k p n mv 3 2 2 2 1 3 2 = ( ) = •理想气体的温度 mv kT 2 3 2 1 2 =
7-4能量均分定理理想气体内能 、 自由度 ●定义: 确定一个物体的空间位置所需要的独 立坐标数目 自由度。 ●质点的自由度 直线运动x 一个自由度 1 平面运动Ky 两个自由度 2 空间运动Xz 三个自由度 =3 ●自由刚体 三个独立的坐标x,y,z决定转轴上一点 两个独立的α,B决定转轴空间位置 A(x,y;) 一个坐标决定刚体转过的角度 =6 3个平动 3个转动
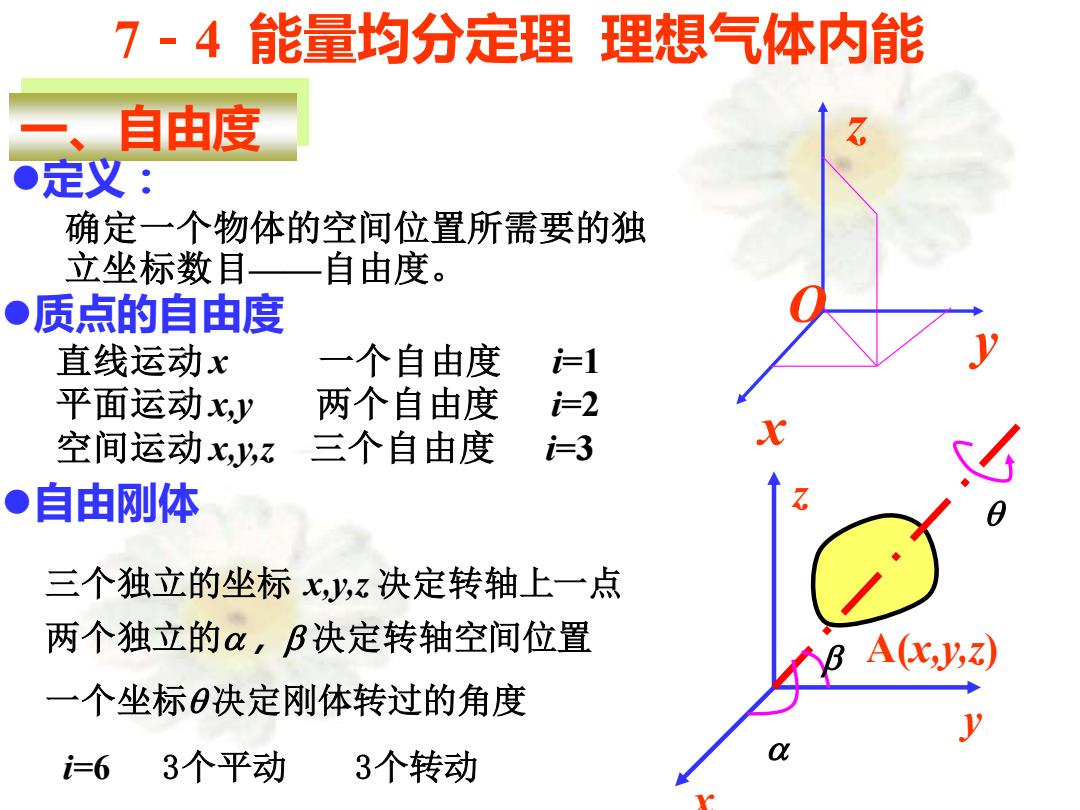
7-4 能量均分定理 理想气体内能 一、自由度 ⚫定义: 确定一个物体的空间位置所需要的独 立坐标数目——自由度。 ⚫质点的自由度 直线运动 x 一个自由度 i=1 平面运动 x,y 两个自由度 i=2 空间运动 x,y,z 三个自由度 i=3 ⚫自由刚体 i=6 3个平动 3个转动 一个坐标q 决定刚体转过的角度 两个独立的a,b 决定转轴空间位置 三个独立的坐标 x,y,z 决定转轴上一点 x y z O A(x,y,z) x y z a b q
●刚性杆: x,y,a,阝i=5 ●刚体定轴转动: 0=1 ●分子的自由度 A(,V,Z) 单原子3自由质点 双原子=5刚性杆 多原子=6自由刚体 ●说明:一般来说,心3个原子组成的分子,共有3个自由度, 其中3个平动自由度,3个转动自由度,(3-6)个振动自由度。当 气体处于低温状态时,可把分子视为刚体
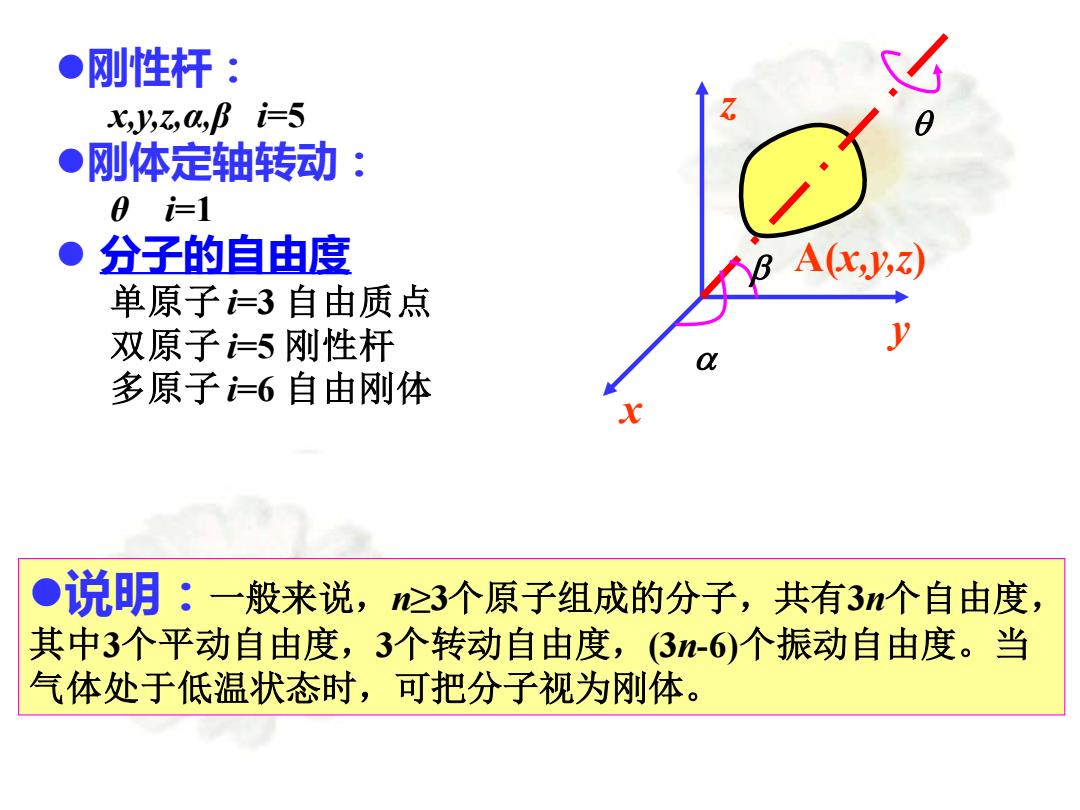
⚫刚性杆: x,y,z,α,β i=5 ⚫刚体定轴转动: θ i=1 ⚫ 分子的自由度 单原子 i=3 自由质点 双原子 i=5 刚性杆 多原子 i=6 自由刚体 ⚫说明:一般来说,n≥3个原子组成的分子,共有3n个自由度, 其中3个平动自由度,3个转动自由度,(3n-6)个振动自由度。当 气体处于低温状态时,可把分子视为刚体。 A(x,y,z) x y z a b q

能量均分定理: 3 一个分子的平均平动能为 kT 2 8=7mv2=)m+m 2 2 2 my 2 =2 = 平方项的平均值 2 2 平动自由度 结论:分子的每一个平动自由度上具有相同的平均平动动 能,都是kT2,或者说分子的平均平动动能3kT2是均匀地 分配在分子的每一个自由度上
⚫ 一个分子的平均平动能为 二、能量均分定理: kt kT 2 3 = 2 2 2 2 2 1 2 1 2 1 2 1 k x y z = mv = mv + mv + mv 2 2 2 2 3 1 v v v v x = y = z = mvx mvy mvz kT 2 1 2 1 2 1 2 1 2 2 2 = = = 结论:分子的每一个平动自由度上具有相同的平均平动动 能,都是kT/2 ,或者说分子的平均平动动能3kT/2是均匀地 分配在分子的每一个自由度上 平方项的平均值 平动自由度

推广:在温度为T的平衡态下,分子的每一个转动自由度 上也具有相同的平均动能,大小也为kT2。 能量按自由度均分定理: 在温度为T的平衡态下,气体分子每个自由度 的平均动能都相等,都等于kT/2。这就是能量 按自由度均分定理,简称能量均分定理。 说明: 8 ·是统计规律,只适用于大量分 单原子分子=3εk=3kT2 子组成的系统。 双原子分子=5εk=5kT2 ·气体分子无规则碰撞的结果。 多原子分子=6εk=6kT12 统计物理可给出严格证明
能量按自由度均分定理: 说明: •是统计规律,只适用于大量分 子组成的系统。 • 气体分子无规则碰撞的结果。 •统计物理可给出严格证明。 推广:在温度为T 的平衡态下,分子的每一个转动自由度 上也具有相同的平均动能,大小也为kT/2。 在温度为T的平衡态下,气体分子每个自由度 的平均动能都相等,都等于kT/2。这就是能量 按自由度均分定理,简称能量均分定理。 单原子分子i=3 εk=3kT/2 双原子分子i=5 εk=5kT/2 多原子分子i=6 εk=6kT/2 kT i k 2 =
三、理想气体的内能和摩尔热容 1、理想气体的内能: ●热力学系统的内能 热力学系统的内能是指气体分子各种形态的动能与势能的总 和。即系统所包含的全部分子的能量总和称为系统的内能。 ●理想气体内能公式 理想气体内能是分子平动动能与转动动能之和 分子的自由度为,则一个 ●说明: 分子能量为kT2,1摩尔理 理想气体的内能与温度和分子的 想气体,有个N4分子,内 自由度有关。 E-AT: •内能仅是温度的函数,即E=E①, 与P,无关。 状态从T1→T2,不论经过什么过程, M摩尔理想气体,内能 内能变化为 E m I RT m I M2 AE=E2-E= R(T2-T1)
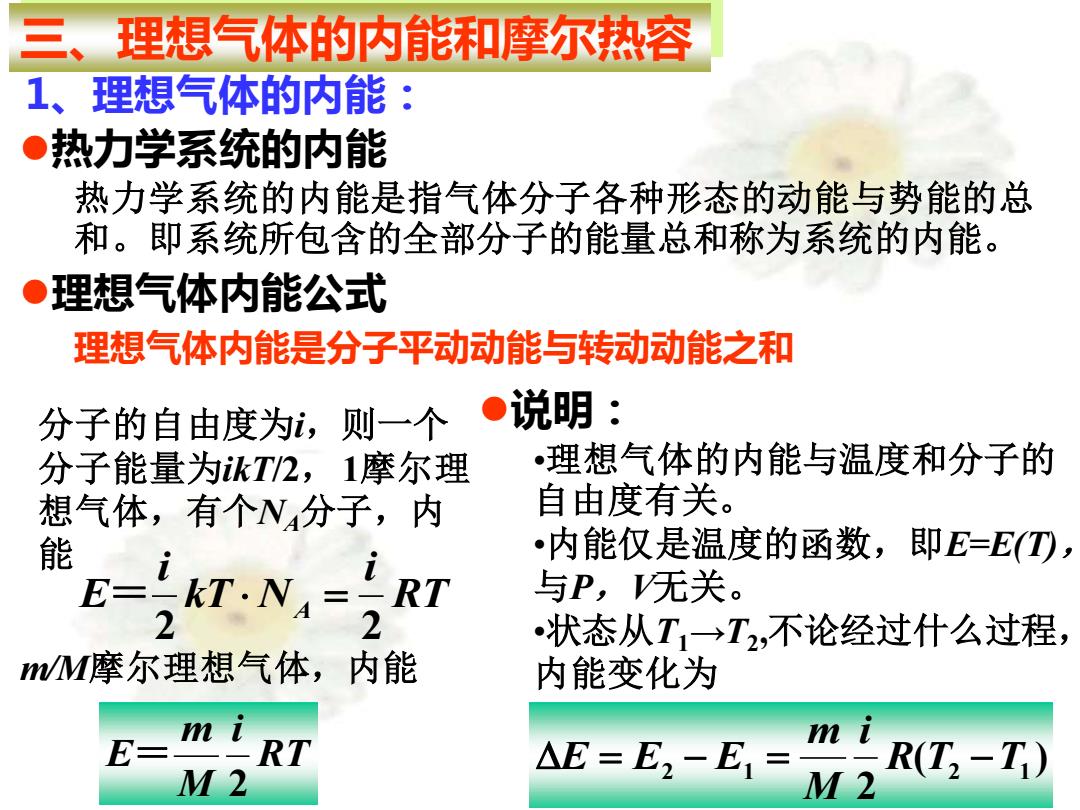
⚫热力学系统的内能 热力学系统的内能是指气体分子各种形态的动能与势能的总 和。即系统所包含的全部分子的能量总和称为系统的内能。 三、理想气体的内能和摩尔热容 1、理想气体的内能: ⚫理想气体内能公式 理想气体内能是分子平动动能与转动动能之和 分子的自由度为i,则一个 分子能量为ikT/2,1摩尔理 想气体,有个NA分子,内 能 RT i kT N i E A 2 2 = = m/M摩尔理想气体,内能 RT i M m E 2 = ⚫说明: •理想气体的内能与温度和分子的 自由度有关。 •内能仅是温度的函数,即E=E(T), 与P,V无关。 •状态从T1→T2 ,不论经过什么过程, 内能变化为 ( ) 2 2 1 R T2 T1 i M m E = E − E = −
2、摩尔热容 R 对于单原子分子与双原子 定体摩尔热容 2 i+2 分子,理论与实验符合得 R 定压摩尔热容 p,m 很好,而对于多原子分子, 2 i+2 理论与实验相差较大。 摩尔热容比 Y= Cp.m 气体 理论值 实验值 Cy叫 Cem Cvm CE.m Y He 12.61 20.95 1.66 12.47 20.78 1.67 Ne 12.53 20.90 1.67 H, 20.47 28.83 1.41 N 20.78 20.09 1.40 20.56 28.88 1.40 02 21.16 29.61 1.40 H,O 27.8 36.2 1.31 CH 24.93 33.24 1.33 27.2 35.2 1.30 CHCI 63.7 72.0 1.13
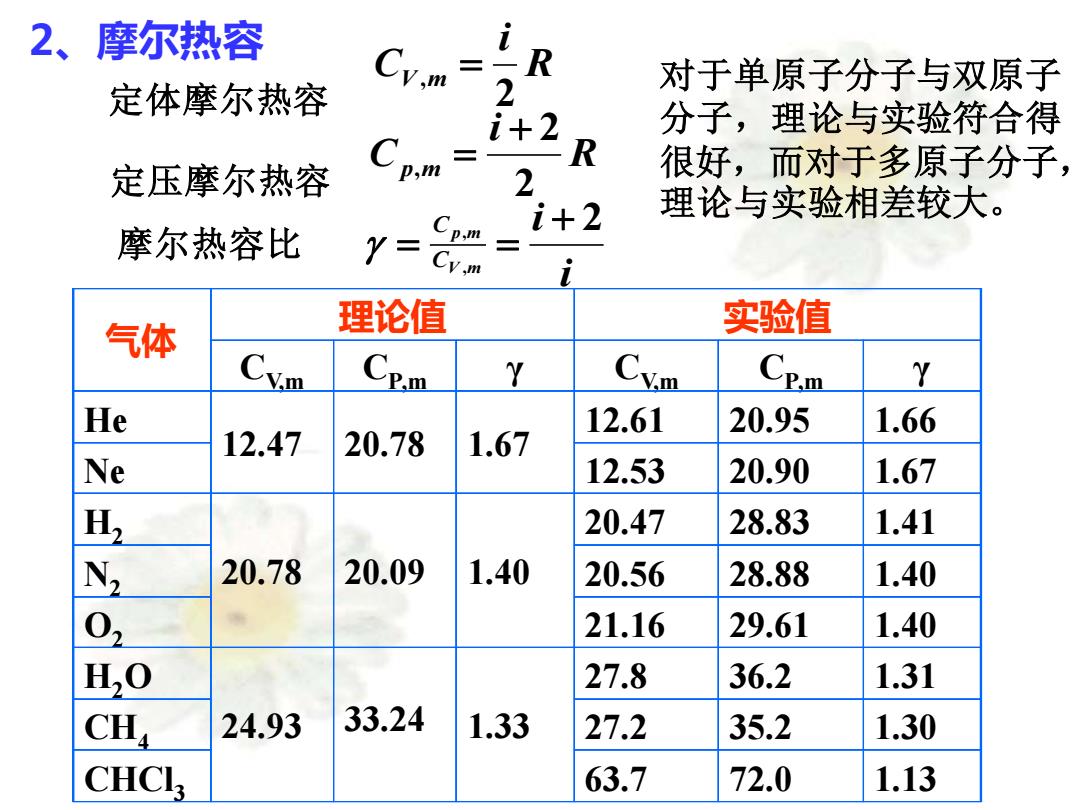
2、摩尔热容 定体摩尔热容 R i CV m 2 , = 定压摩尔热容 R i Cp m 2 2 , + = 摩尔热容比 i i V m p m C C 2 , , + = = 气体 理论值 实验值 CV,m CP,m γ CV,m CP,m γ He 12.47 20.78 1.67 12.61 20.95 1.66 Ne 12.53 20.90 1.67 H2 20.78 20.09 1.40 20.47 28.83 1.41 N2 20.56 28.88 1.40 O2 21.16 29.61 1.40 H2O 24.93 33.24 1.33 27.8 36.2 1.31 CH4 27.2 35.2 1.30 CHCl3 63.7 72.0 1.13 对于单原子分子与双原子 分子,理论与实验符合得 很好,而对于多原子分子, 理论与实验相差较大

四、固体热容 设固体由N个原子组成,N个原子的三维振动,可以看成 是3N个一维振动。原子作一维振动时,自由度为2,一项 为动能,一项为势能。N个原子振动的平均能量为 E=3NE=3NkT 1mol晶体的内能为 E=3N kT=3RT 晶体的摩尔热容 do =3R dT dT =25.1J.mol-1.K-1
四、固体热容 设固体由N个原子组成,N个原子的三维振动,可以看成 是3N个一维振动。原子作一维振动时,自由度为i=2,一项 为动能,一项为势能。N个原子振动的平均能量为 E = 3N = 3NkT 1mol晶体的内能为 E = 3NA kT = 3RT 晶体的摩尔热容 1 1 25.1 3 − − = = = = J mol K R dT dE dT dQ Cm

7·5麦克斯韦气体速率分布律 引言: 气体分子处于无规则的热运动之中,由于碰撞,每个分 子的速度都在不断地改变,所以在某一时刻,对某个分 子来说,其速度的大小和方向完全是偶然的。然而就大 量分子整体而言,在一定条件下,分子的速率分布遵守 一 定的统计规律— 气体速率分布律。 气体分子按速率分布的统计规律最早是有麦克斯韦于1859年 在概率论的基础上导出的,1877年玻耳兹曼由经典统计力学 中导出,1920年斯特恩从实验中证实了麦克斯韦分子按速率 分布的统计规律
7-5 麦克斯韦气体速率分布律 引言: 气体分子处于无规则的热运动之中,由于碰撞,每个分 子的速度都在不断地改变,所以在某一时刻,对某个分 子来说,其速度的大小和方向完全是偶然的。然而就大 量分子整体而言,在一定条件下,分子的速率分布遵守 一定的统计规律——气体速率分布律。 气体分子按速率分布的统计规律最早是有麦克斯韦于1859年 在概率论的基础上导出的,1877年玻耳兹曼由经典统计力学 中导出,1920年斯特恩从实验中证实了麦克斯韦分子按速率 分布的统计规律