
海大理学院赦学课件 大学物理学电子教案 刚体力学习题课
大学物理学电子教案 海大理学院教学课件 刚体力学习题课

1.对应 线量 角量 位置矢量 角位置 位 移 △产 角位移 △0 dr de 速 度 节= dt 角速度 dt dy d'r do d20 加速度 Q= 角加速度 a= dt dt2 dt dr2 =Vo at 0=0o+d S-So=Vot+ 2 8-0。=m,t+ 2 v2-vi=2a(s-so) o2-0=2a(0-0) 质 量 m 转动惯量 J 力 示 力 矩 M 牛顿定律 F=ma M=Ja 转动定律 动 能 1 Jω2 2 mv2 转动动能 2
1. 对应线 量 位置矢量 位 移 速 度 加 速 度 2 2 dt d r dt dv a dt dr v r r = = = 角 位 置 角 位 移 角 速 度 角加速度 2 2 dt d dt d dt d = = = 2 ( ) 2 1 0 2 0 2 2 0 0 0 v v a s s s s v t at v v at − = − − = + = + 2 ( ) 2 1 0 2 0 2 2 0 0 0 − = − − = + = + t t t 质 量 力 牛顿定律 动 能 2 2 1 mv F ma F m = 转动惯量 力 矩 转动定律 转动动能 2 2 1 J M J M J = 角 量
平动与转动的对应关系 平动 转动 动量 mv 动量矩 Io 动量定理 动量矩定理 冲量=「Fdt=mv-mv。 冲量=∫Mh=Jo-Jo, 动量守恒定理 动量矩守恒定理 条件 ∑F外=0 条件 ∑M外=0 ∑mm=恒量 ∑Jm=恒量 动能定理 动能定理 w-fFdr-m-mi 机械能守恒定律 条件:W外+W非=0(或只有保守力作功 2+w+脑g+号=恒量
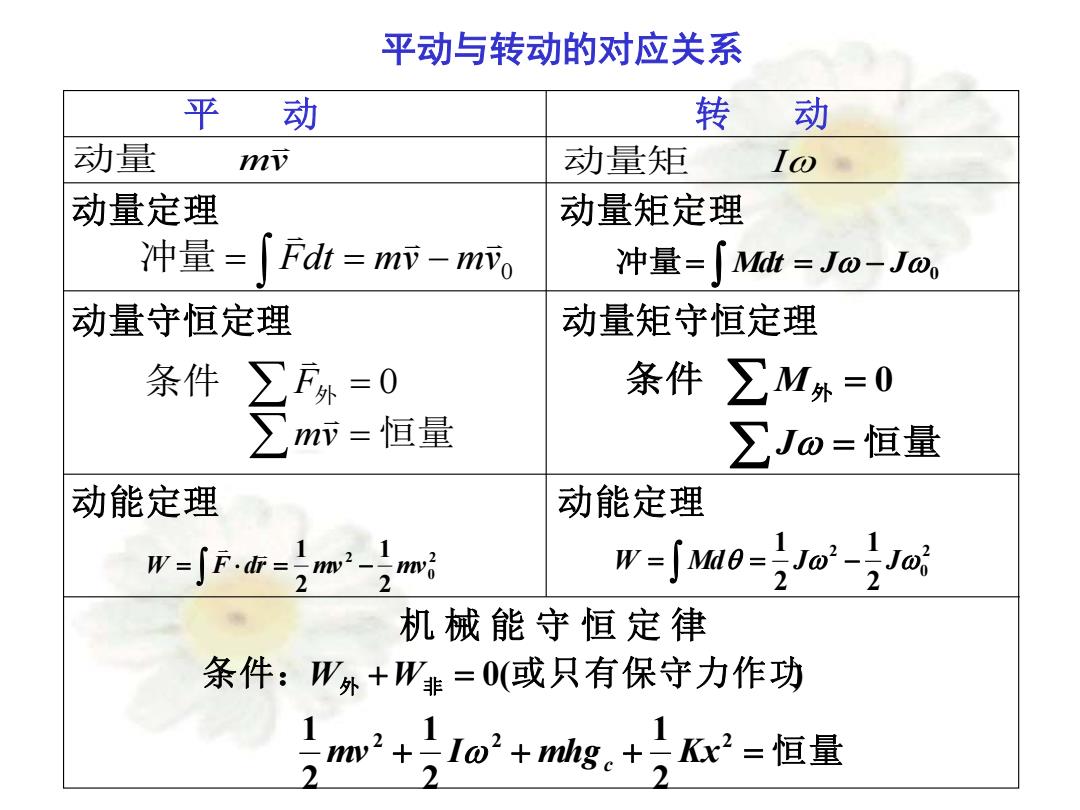
平动与转动的对应关系 平 动 mv 动量 动量定理 0 Fdt mv mv = = − 冲量 动量守恒定理 = = 恒量 条件 外 J M 0 动能定理 2 0 2 2 1 2 1 W = F dr = mv − mv 机 械 能 守 恒 定 律 恒 量 条件: 外 非 或只有保守力作功 + + + = + = 2 2 2 2 1 2 1 2 1 0( ) mv I mhg Kx W W c 转 动 动量矩 I 动量矩定理 冲量= Mdt = J − J0 动量矩守恒定理 = = 恒量 条件 外 mv F 0 动能定理 2 0 2 2 1 2 1 W = Md = J − J

◆基本概念 转动惯量J.=∑△m 角动量L=J0 动力学特点 ◆刚体 转动定 M外z=Jz0 定轴转 律 动的特 点 外力矩所做的总功 W外a∫M6外d0 功能 特 转动动能定 m2=)Jo,2-a 理 重力势能:E。=mgh。转动动 Ek=Jo? 2 能 ◆其它规律与普通的质点系一样
= ⊥ i z i i J m r 转动惯量 2 基本概念 其它规律与普通的质点系一样 刚体 定轴转 动的特 点 W M d 外力矩所做的总功 外总 = 合外 转动动能定 理 2 1 2 12 2 2 1 2 1 W = J − J 重力势能: Ep = mghc 转动动 能 2 2 1 Ek = J 功能 特点 转动定 M外z = Jz 律 动力学特点 角动量 L z = Jz

1、有两个力作用在一个有固定轴的刚体上 (1)这两个力都平行于轴作用时,它们对轴的合力矩一定为0。 (2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是0。 (3)当这两个力的合力为0时,它们对轴的合力矩也一定为0。 (4)当这两个力对轴的合力矩为0时,它们的合力也一定是0。 答:(1)、(2):正确 (3)、(4):不正确
1、有两个力作用在一个有固定轴的刚体上 (1) 这两个力都平行于轴作用时,它们对轴的合力矩一定为 0。 (2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是0。 (3) 当这两个力的合力为 0 时,它们对轴的合力矩也一定为 0。 (4) 当这两个力对轴的合力矩为 0 时,它们的合力也一定是 0。 答:(1)、(2): 正确 (3)、(4): 不正确

2、一光滑的圆环绕竖直轴(转动惯量J0)以角速度⊙o旋转, 一静止小球从顶端开始下滑,求小球各点角速度和速度。 解:m+环:对竖直轴的角动量守恒 A ☒R(sin)o Jo@+mR2 sin200=Jo@o 00 R B 0= mR2 sin20 1+ J m+环十地球:机械能守恒,A为势能零点 2J=-mgR(1-cos0)+Jo+1 1 +。mw2 J=J。+mR2sin20 v2=2gR(1-c0s0)+4 R2sin20 1 mR2sin20 Jo
2、一光滑的圆环绕竖直轴(转动惯量 J0 )以角速度 0 旋转, 一静止小球m 从顶 端开始下滑,求小球各点角速度和速度。 J mR J mR J 0 2 2 0 0 0 2 2 0 1 + = = + sin sin 2 2 0 2 2 2 0 0 sin 2 1 2 1 (1 cos ) 2 1 J = −mgR − + J + m v J = J + m R v gR R mR J 2 0 2 2 2 2 2 0 2 1 1 = − + + ( cos ) sin sin 解:m+环:对竖直轴的角动量守恒 m+环+地球:机械能守恒,A为势能零点 R A B C ╳ v R(sin)

v2=2gR(1-cos8)+ Rsin0 00 1+mR'sin20 1+mR'sin0 Jo y抽v2+R2sin20w2 讨论:1)小球向下滑动的过程中,动量守恒否? 2)小球向下滑动的过程中,对旋转轴的角动量守恒否? 3)为什么小球的速度里,有o及0项?
讨论:1) 小球向下滑动的过程中,动量守恒否? 2)小球向下滑动的过程中,对旋转轴的角动量守恒否? 3) 为什么小球的速度里,有 及 项? 0 2 2 0 sin 1 J mR + v gR = R mR J 2 0 2 2 2 2 2 0 2 1 1 = − + + ( cos ) sin sin 2 2 2 2 v 地 = v + R sin

3、两小球质量分别为和M,放在半径R的水平光滑大圆环形 轨道上,用线将二球缚住,一弹簧压缩在两球之间。 1) 线剪断,两球弹出,弹簧仍在原处,两球何处相碰? 2)设原来弹簧势能U,线断后何时相碰? 解:1)对O轴角动量守恒 M R MR2=mR2@ (1) m 设M转过p后与m相遇 ①t=p (2)0t=2π-p (3) 由(1)2)3)得: 2nm 0M2π-p p= m+M 2)机械能守恒 IMRQ+mRo'-U 、(4) 2mM 由(1)2)3)(4得: t= =TR (m+M)Uo
3、两小球质量分别为m和M,放在半径R的水平光滑大圆环形 轨道上,用线将二球缚住,一弹簧压缩在两球之间。 1)线剪断,两球弹出,弹簧仍在原处,两球何处相碰? 2)设原来弹簧势能U0,线断后何时相碰? M m R j O m M m + = j 2 解:1)对O轴角动量守恒 2 2 MR = mR (1) t =j t = 2 −j 设 M 转过 j 后与m相遇 (2) (3) j j − = = M 2 m 由 (1)(2)(3)得: 2)机械能守恒 0 2 2 2 2 2 1 2 1 MR + mR =U (4) 0 ( ) 2 m M U mM t R + = = j 由 (1)(2)(3)(4)得:

讨论:绳子剪断前后,动量守恒否? 4、如图,原来它们沿同一转向分别以。0、02匀速转动, 然后,平移两轴,使它们的边缘相接触。 求:最后在接触处无相对滑动时,每个圆柱的角速度@1、®2 解:无相对滑动时,二圆柱 020 ①10 线速度一样: 0R1=02R2 R2y02 (1 两圆柱系统角动量守恒: 0oJ1+02J2=0J1+02J2 由(①2式,可求出0、o:1-MR:-MR (2) 问题:解法正确否?
讨论:绳子剪断前后,动量守恒否? 4、 如图,原来它们沿同一转向分别以10、20匀速转动, 然后,平移两轴,使它们的边缘相接触。 求:最后在接触处无相对滑动时,每个圆柱的角速度1、 2 O1 O2 R1 R2 10 20 解:无相对滑动时,二圆柱 线速度一样: 1 R1 =2 R2 两圆柱系统角动量守恒: 2 2 2 2 2 1 1 1 10 1 20 2 1 1 2 2 2 1 2 1 J M R J M R J J J J = = + = + (1) 由 (2) (1)(2)式,可求出1、 2 问题:解法正确否?

正确解: 无相对滑动时,二圆柱,角速度相反,线速度 一样,以01为正方向 020 010 01R1=02R2 (1) R2/02 R 对两柱分别用角动量定理(合外力矩 都是接触处的摩擦力f): -∫Rf=J1(o-oo) o1☒ 正方向 -R2ft=J2(-o2-020) 0,⊙ R=J1(0,-0) (2) 由(1)2) :0.-Mihom-M.R R(M1+M2) R2J2(-02-020) M1R010-M2R2020 R2(M1+M2)
正确解: 无相对滑动时,二圆柱,角速度相反,线速度 一样,以 1 为正方向 对两柱分别用角动量定理(合外力矩 都是接触处的摩擦力f ): O1 O2 R1 R2 10 20 1 ╳ 2 • − R1 fdt = J1 (1 −10 ) 正方向 − = (− − ) 2 2 2 20 R fdt J 1 R1 =2 R2 (1) ( ) ( ) 2 2 20 1 1 10 2 1 − − − = J J R R (2) 由 (1)(2)得: ( ) 1 1 2 1 1 10 2 2 20 1 R M M M R M R + − = ( ) 2 1 2 1 1 10 2 2 20 2 R M M M R M R + − =