
海大理学院赦学裸件 大学物理学电子教案 刚体的转动(2) 4-2转动定律 4-3角动量 角动量守恒定律
大学物理学电子教案 海大理学院教学课件 刚体的转动(2) 4-2 转动定律 4-3 角动量 角动量守恒定律

复习 刚体的概念 刚体的运动 平动和转动 描述刚体转动的物理量 角速度和角加速度 do do d0 dt Q= dt dt2 力矩 M=F×F 转动定律 M=Ja 转动惯量 J=∑Am,J=jrdm
复 习 刚体的概念 刚体的运动——平动和转动 描述刚体转动的物理量——角速度和角加速度 dt d = 2 2 dt d dt d = = 力矩 M r F = 转动定律 M = J 转动惯量 J = r dm2 i i i J m r = 2

4·2力矩转动定律转动惯量(下) 五、刚体定轴转动的转动定律的应用 题目类型 解题步骤 已知两个物理量,求另一个: 1.确定研究对象; 1.己知J和M,求o 2.受力分析; 2.已知J和,求M 3选择参考系与坐标系; 3.已知M和,求J 4.列运动方程; 5.解方程; 6.必要时进行讨论。 注意以下几点: 1.力矩与转动惯量必须对同一转轴而言的; 2.要选定转轴的正方向,以便确定已知力矩或角加速度、角 速度的正负; 3.系统中有转动和平动, 转动物体 转动定律 平动物体 牛顿定律
五、刚体定轴转动的转动定律的应用 题目类型 已知两个物理量,求另一个: 1.已知J和M,求 2.已知J和 ,求M 3.已知M和,求J 解题步骤 1.确定研究对象; 2.受力分析; 3.选择参考系与坐标系; 4.列运动方程; 5.解方程; 6.必要时进行讨论。 注意以下几点: 1.力矩与转动惯量必须对同一转轴而言的; 2.要选定转轴的正方向,以便确定已知力矩或角加速度、角 速度的正负; 3. 系统中有转动和平动, 转动物体——转动定律 平动物体——牛顿定律 4-2 力矩 转动定律 转动惯量(下)
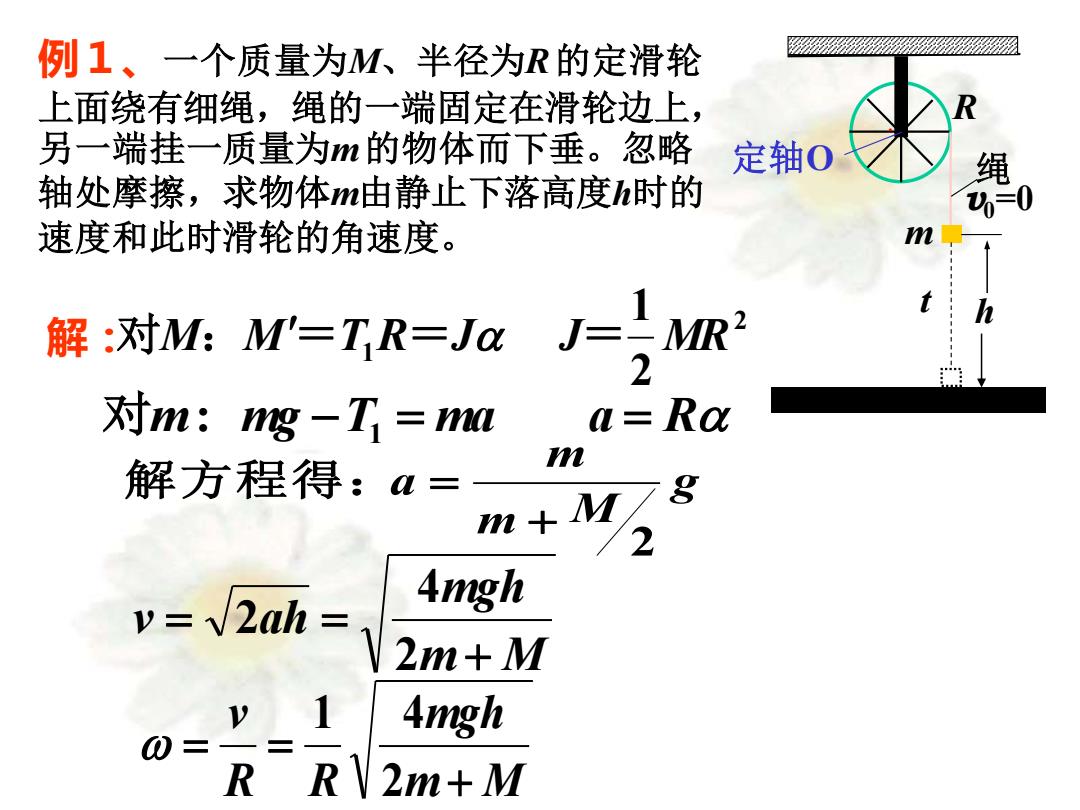
例1、一个质量为M、半径为R的定滑轮 上面绕有细绳,绳的一端固定在滑轮边上, 另一端挂一质量为m的物体而下垂。忽略 定轴0 轴处摩擦,求物体m由静止下落高度h时的 速度和此时滑轮的角速度。 解:对M:M'=TR=Ja J=MR2 对m:g-T=mm a=Ra 解方程得:a= m+M 12 4mgh 2m+M 1 4mgh 0= R R\2m+M
例1、一个质量为M、半径为R 的定滑轮 上面绕有细绳,绳的一端固定在滑轮边上, 另一端挂一质量为m 的物体而下垂。忽略 轴处摩擦,求物体m由静止下落高度h时的 速度和此时滑轮的角速度。 解: 对m: mg −T1 = ma a = R 2 1 2 1 对M:M=T R=J J= MR m M mgh R R v + = = 2 1 4 2 4 2 m M mgh v ah + = = g m M m a 2 + 解方程得: = 定轴O · R t h m v0=0 绳

例2、一根长为l、质量为m的均匀细直棒,其一端有一固定的 光滑水平轴,因而可以在竖直平面内转动。最初棒静止在水平 位置,求它由此下摆日角时的角加速度和角速度。 解:棒下摆为加速过程,外 力矩为重力对0的力矩。棒 X 上取质元dm,当棒处在下摆0 dm 角时,重力矩为: M=∫gxdm=gxdm dmg 据质心定义「xdm=xc 1 ..M=mgxc M- 、ngl cos 0 2 1 1 七。=。lcos mgl cosO 2 M 2 3gcose Q= J 1 21 3
例2、一根长为l、质量为m 的均匀细直棒,其一端有一固定的 光滑水平轴,因而可以在竖直平面内转动。最初棒静止在水平 位置,求它由此下摆角时的角加速度和角速度。 解:棒下摆为加速过程,外 力矩为重力对O 的力矩。 棒 上取质元dm,当棒处在下摆 角时,重力矩为: M= gxdm = g xdm X O dmg dm x M = mgxC 据质心定义 xdm = mxc cos 2 1 x l c = cos 2 1 M = mgl l g ml mgl J M 2 3 cos 3 1 cos 2 1 2 = = =
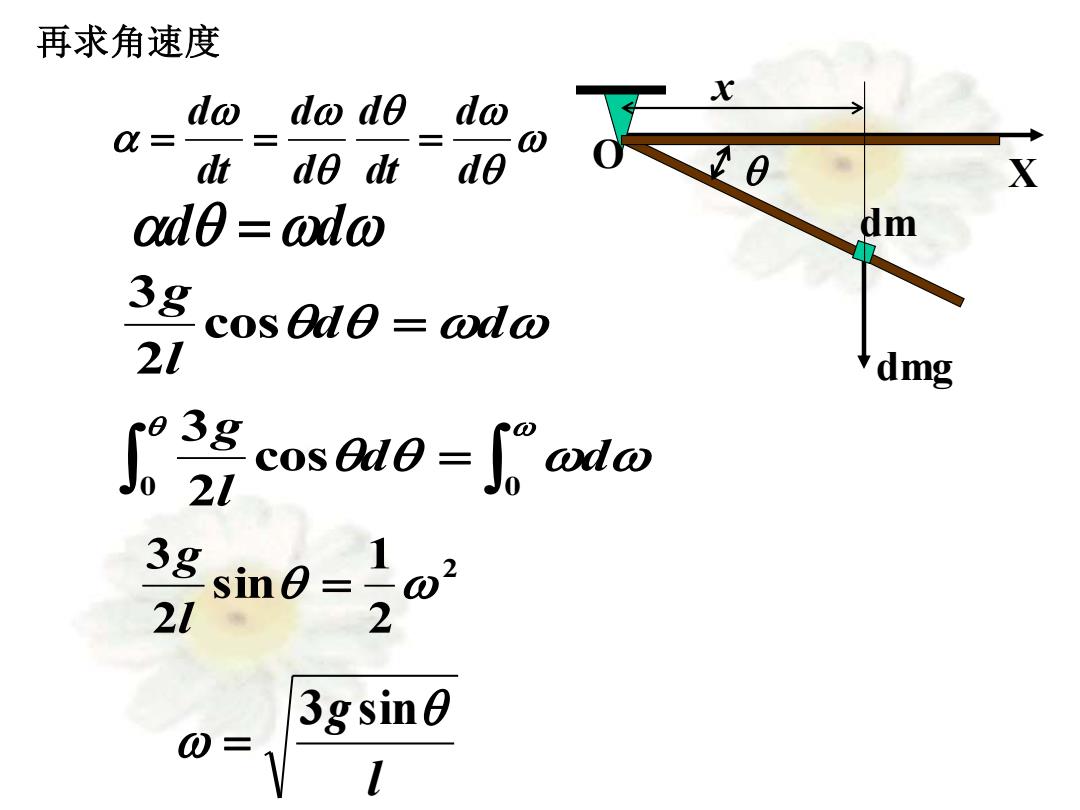
再求角速度 do dw do do Q= dt d0 dt X ad0 adw d m 3g cos ede=axda 21 dmg osaro- 3gsin0=201 21 2 3gsin 0=
dd dt d dd dt d = = = d d lg cos = 23 = 0 0 cos 23 d d lg 2 21 sin 23 = lg l g 3 sin = d = d 再求角速度 X O dmg dm x
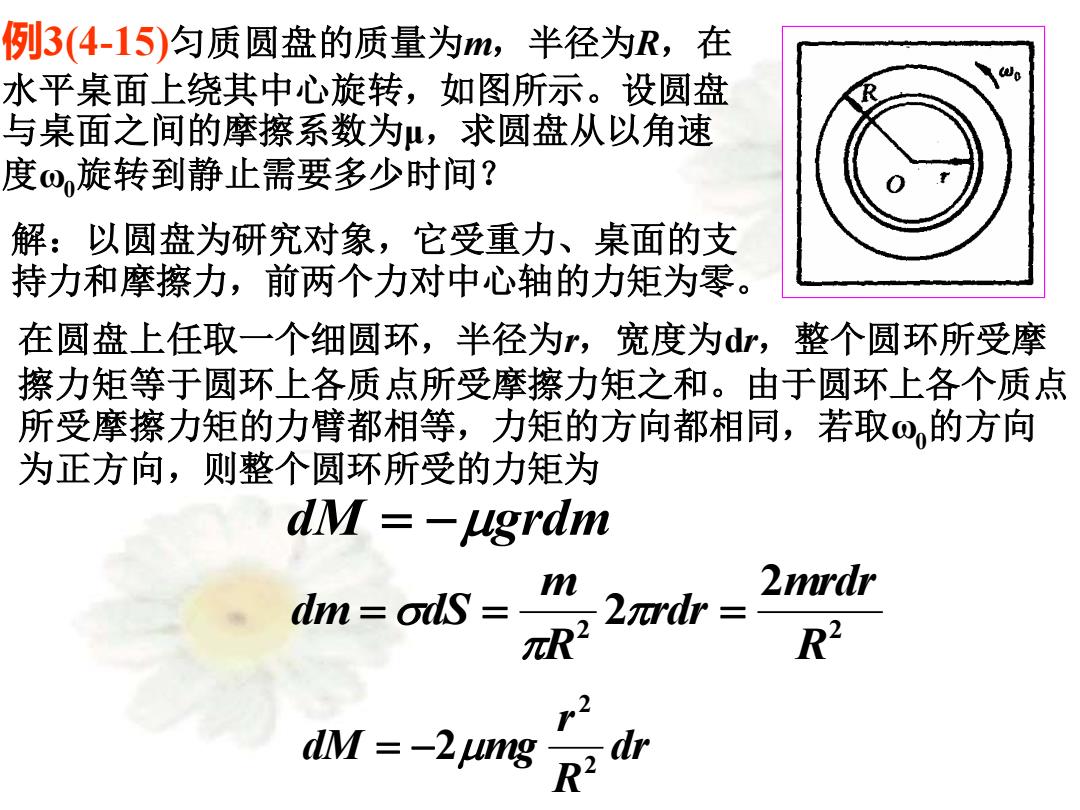
例3(4-15)匀质圆盘的质量为m,半径为R,在 水平桌面上绕其中心旋转,如图所示。设圆盘 与桌面之间的摩擦系数为μ,求圆盘从以角速 度o,旋转到静止需要多少时间? 解:以圆盘为研究对象,它受重力、桌面的支 持力和摩擦力,前两个力对中心轴的力矩为零。 在圆盘上任取一个细圆环,半径为r,宽度为,整个圆环所受摩 擦力矩等于圆环上各质点所受摩擦力矩之和。由于圆环上各个质点 所受摩擦力矩的力臂都相等,力矩的方向都相同,若取Q,的方向 为正方向,则整个圆环所受的力矩为 dM =-ugrdm n 2mrdr dm ods R2 2ardr R2 六2 dM =-2umg
例3(4-15)匀质圆盘的质量为m,半径为R,在 水平桌面上绕其中心旋转,如图所示。设圆盘 与桌面之间的摩擦系数为μ,求圆盘从以角速 度ω0旋转到静止需要多少时间? 解:以圆盘为研究对象,它受重力、桌面的支 持力和摩擦力,前两个力对中心轴的力矩为零。 在圆盘上任取一个细圆环,半径为r,宽度为dr,整个圆环所受摩 擦力矩等于圆环上各质点所受摩擦力矩之和。由于圆环上各个质点 所受摩擦力矩的力臂都相等,力矩的方向都相同,若取ω0的方向 为正方向,则整个圆环所受的力矩为 dM = −grdm2 2 2 2 R mrdr rdr R m dm = dS = = dr R r dM mg 2 2 = −2

整个圆盘所受的力矩为 R 2 M=∫-2gd=- 0 根据转动定律,得 2 M MmgR 48 a 3 mR2 3R 2 角加速度为常量,且与Q,的方向相反,表明圆盘作匀减速转动 0=00+0t 当圆盘停止转动时,0=0,则得 3R00 a Aug
整个圆盘所受的力矩为 dr mgR R r M mg R 3 2 2 0 2 2 = − = − 根据转动定律,得 R g mR mgR J M 3 4 2 1 3 2 2 = − − = = 角加速度为常量,且与ω0的方向相反,表明圆盘作匀减速转动 = +t 0 当圆盘停止转动时,ω=0,则得 g R t 4 0 3 0 = − =
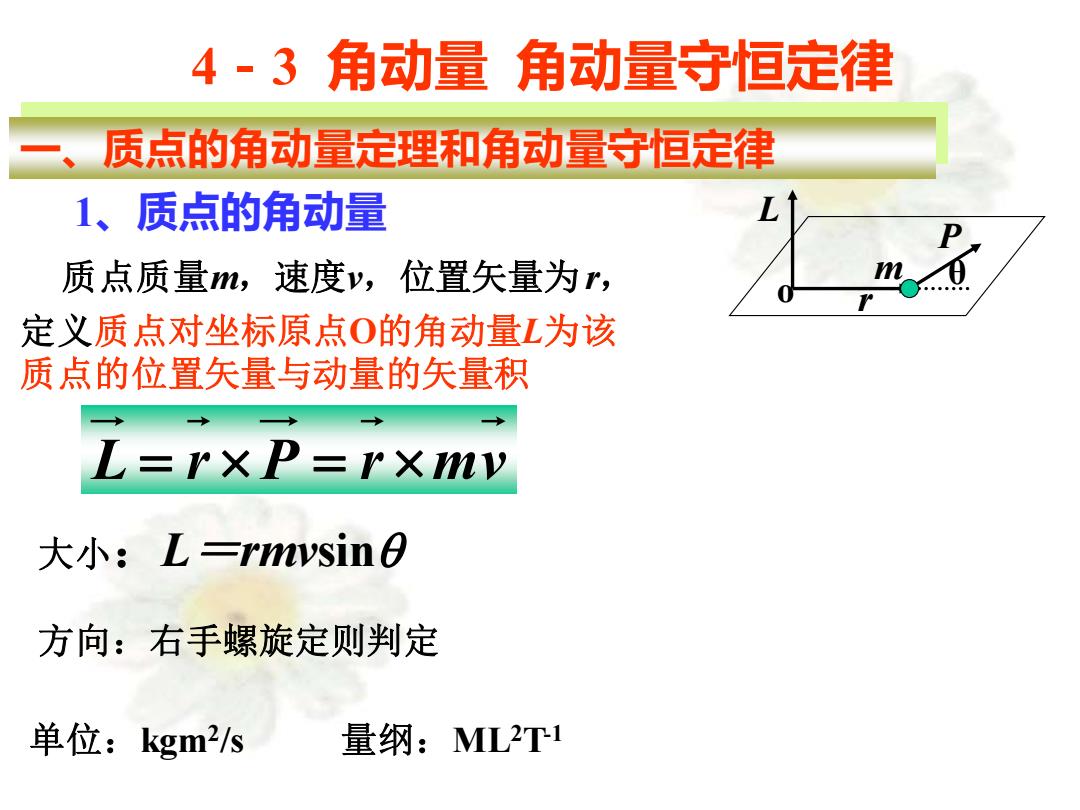
4-3角动量角动量守恒定律 质点的角动量定理和角动量守恒定律 1、质点的角动量 质点质量m,速度y,位置矢量为r, 定义质点对坐标原点O的角动量L为该 质点的位置矢量与动量的矢量积 L=rxP=rxmv 大小:L=rmysin O 方向:右手螺旋定则判定 单位:kgm2s 量纲:ML2T1
4-3 角动量 角动量守恒定律 一、质点的角动量定理和角动量守恒定律 1、质点的角动量 m o r P L θ L = r P = r mv 大小:L=rmvsin 方向:右手螺旋定则判定 单位:kgm2 /s 量纲:ML2T-1 质点质量m,速度v,位置矢量为r, 定义质点对坐标原点O的角动量L为该 质点的位置矢量与动量的矢量积
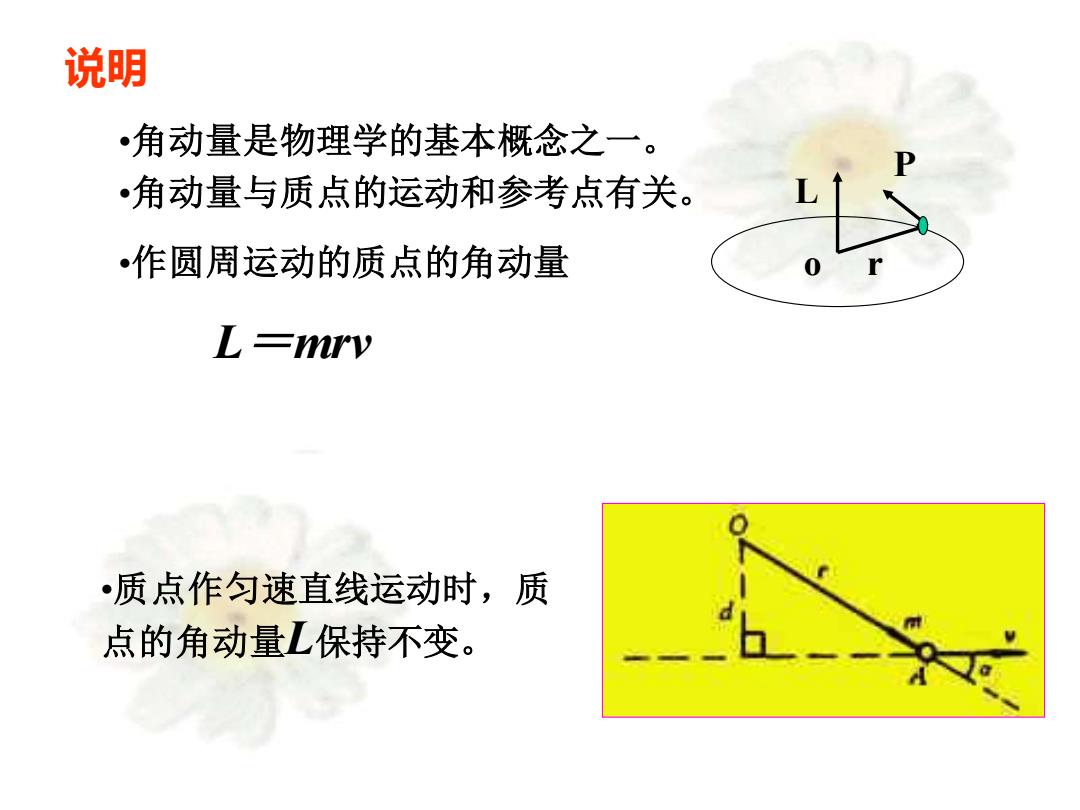
说明 •角动量是物理学的基本概念之一。 •角动量与质点的运动和参考点有关。 •作圆周运动的质点的角动量 L=mry •质点作匀速直线运动时,质 点的角动量L保持不变
说明 •角动量是物理学的基本概念之一。 •角动量与质点的运动和参考点有关。 •作圆周运动的质点的角动量 L=mrv •质点作匀速直线运动时,质 点的角动量L保持不变。 P L o r