
海大理学院教学裸件, 大学物理学电子教案 机械能与机械能守恒定律 3-7完全弹性碰撞完全非弹性碰掊 3-8能量守恒定律 3-9质心质心运动定律
3-7 完全弹性碰撞 完全非弹性碰撞 3-8 能量守恒定律 3-9 质心 质心运动定律 大学物理学电子教案 海大理学院教学课件 机械能与机械能守恒定律

复习 势能 重力势能Ep=gy 功与功率dW=F.dS Mm 引力势能E。=-G P dW dt 1 弹性势能 E=mc2 质点的动能定理 2 ·质点系的动能定理 2 W=二w 2 2 2%,=2Ea-2Em 万有引力、重力、 弹性力 作功的特点 质点系的功能原理 物体沿任意闭合路径运行一 W外力十W非保守外为一E一E, 周时,保守力对它所作的功 为零。 机械能守恒定律 2E。+2Ew-2En+2E
复习 •功与功率 dW F dS = dt dW P= •质点的动能定理 2 1 2 2 2 1 2 1 W = mv − mv •万有引力、重力、弹性力 作功的特点 物体沿任意闭合路径运行一 周时,保守力对它所作的功 为零。 •势能 E mgy p = r Mm Ep = −G 2 2 1 Ep = mx 重力势能 引力势能 弹性势能 •质点系的动能定理 = = = = − n i ki n i ki n i Wi E E 1 0 1 1 •质点系的功能原理 W外 力+W非保守外力 =E-E0 •机械能守恒定律 = = = = + + n i p i n i k i n i p i n i Ek i E E E 0 0 0 0 0 0 =
3-7完全弹性碰撞 完全非弹性碰撞 碰撞 1、概念 两个或两个以上的物体相遇,且相 互作用持续一个极短暂的时间 碰撞。 2、特点 •物体间的相互作用是突发性,持续 时间极短。 •作用力峰值极大,碰撞符合动量守 恒定律的适用条件。 1 0 碰撞过程中物体会产生形变
3-7 完全弹性碰撞 完全非弹性碰撞 一、碰撞 1、概念 两个或两个以上的物体相遇,且相 互作用持续一个极短暂的时间—— 碰撞。 2、特点 •物体间的相互作用是突发性,持续 时间极短。 •作用力峰值极大,碰撞符合动量守 恒定律的适用条件。 •碰撞过程中物体会产生形变

3、碰撞过程的分析 Uio D2o 接触阶段: 两球对心接近运动 形变产生阶段:两球相互挤压,最后两球速度相同 动能转变为势能 形变恢复阶段:在弹性力作用下两球速度逐渐不同而分 开运动 势能转变为动能 分离阶段: 两球分离,各自以不同的速度运动 4、分类 完全弹性碰撞: 系统动能守恒 非弹性碰撞: 系统动能不守恒 完全非弹性碰撞:系统以相同的速度运动
3、碰撞过程的分析 接触阶段: 两球对心接近运动 形变产生阶段:两球相互挤压,最后两球速度相同—— 动能转变为势能 形变恢复阶段:在弹性力作用下两球速度逐渐不同而分 开运动——势能转变为动能 分离阶段: 两球分离,各自以不同的速度运动 4、分类 •完全弹性碰撞: 系统动能守恒 •非弹性碰撞: 系统动能不守恒 •完全非弹性碰撞: 系统以相同的速度运动

完全弹性碰撞 碰撞前 1、碰撞前后速度的变化 两球m1,m2对心碰撞,碰撞 碰撞后 前速度分别为y10、y20,碰撞 后速度变为y、2 动量守恒 m1y1+m2'2=my1o+m2V20 (1 1 2 (2) 2 2 2 由上面两式可得 m (v,-vio)=mz(v2o-v2) 3) m2-呢)=m,2-) (4)
二、完全弹性碰撞 1、碰撞前后速度的变化 两球m1,m2对心碰撞,碰撞 前速度分别为v10、v20,碰撞 后速度变为v1、v2 动量守恒 (1) 1 1 2 2 1 10 2 20 m v + m v = m v + m v (2) 2 1 2 1 2 1 2 1 2 2 20 2 1 10 2 2 2 2 1 1 m v + m v = m v + m v 由上面两式可得 ( ) ( ) (3) 1 1 10 2 20 2 m v − v = m v − v ( ) ( ) (4) 2 2 2 2 2 0 2 1 0 2 1 1 m v − v = m v − v

(4)/3)得 y1+y10=V2+V20 V10-V20=V2-V1 碰撞前两球相互趋近的相对速度(y10-20)等于碰撞后两球相 互分开的相对速度(2-1) 由(3)、(5)式可以解出 m1-m21o+2m2y20 V1= m1+m2 (m2-m1少2o+2my0 V2= m1+m2
(4)/(3)得 (5) 1 0 2 0 2 1 1 1 0 2 2 0 v v v v v v v v - = - + = + 碰撞前两球相互趋近的相对速度(v10-v20)等于碰撞后两球相 互分开的相对速度(v2 -v1) 由(3)、(5)式可以解出 ( ) ( ) 1 2 2 1 2 0 1 1 0 2 1 2 1 2 1 0 2 2 0 1 2 2 m m m m v m v v m m m m v m v v + − + = + − + =

2、讨论 ·若m=,则y=y2o,”2=yo,两球碰撞时交换速度。 若y20=0,m1<h2,则y1≈-y1,y20,m1反弹, 即质量很大且原来静止的物体,在碰撞后仍保持不 动,质量小的物体碰撞后速度等值反向。 ·若m2<m1,且y20=0,则y1y10’22y10, 即一个质量很大的球体,当它的与质量很小的球体 相碰时,它的速度不发生显著的改变,但是质量很 小的球却以近似于两倍于大球体的速度运动
2、讨论 •若m1=m2,则v1=v20,v2=v10,两球碰撞时交换速度。 •若v20=0,m1<<m2,则v1≈ - v1,v2=0,m1反弹, 即质量很大且原来静止的物体,在碰撞后仍保持不 动,质量小的物体碰撞后速度等值反向。 •若m2<<m1,且v20=0,则v1≈v10,v2≈2v10, 即一个质量很大的球体,当它的与质量很小的球体 相碰时,它的速度不发生显著的改变,但是质量很 小的球却以近似于两倍于大球体的速度运动

三、完全非弹性碰撞 碰撞后系统以相同的速度运动 V=V2=V 动量守恒 1y10+m2y20=(m1+m2)y m vio+m2v20 v= m1+m2 动能损失为 aE-行%品+m吃m+m加 网-
三、完全非弹性碰撞 碰撞后系统以相同的速度运动 v1=v2 =v 动量守恒 m v m v (m m )v 1 10 + 2 20 = 1 + 2 1 2 1 10 2 20 m m m v m v v + + = 动能损失为 ( ) ( ) ( ) 2 1 0 2 0 1 2 1 1 2 1 2 2 2 2 0 2 1 1 0 2 2 1 2 1 2 1 v v m m m m E m v m v m m v − + = − + = +

四、非完全弹性碰撞 恢复系数 牛顿提出碰撞定律:碰撞后两球的分离速度y2-与碰撞前 两球的接近速度yo-20之比为以定值,比值由两球材料得性 质决定。该比值称为恢复系数。 V2-y1 e= y10-V20 完全非弹性碰撞: m -emz )vo+(1+e)m2v2o e=0,y2=V1 V1= m1+m2 完全弹性碰撞: (mz em )vzo +(1+e)myio e=1,y2-y1=y10-20 非完全弹性碰撞: m1+m2 0<e<1
四、非完全弹性碰撞 恢复系数 牛顿提出碰撞定律:碰撞后两球的分离速度v2 -v1与碰撞前 两球的接近速度v10-v20之比为以定值,比值由两球材料得性 质决定。该比值称为恢复系数。 10 20 2 1 v v v v e − − = ( ) ( ) 1 2 2 1 2 0 1 1 0 2 1 2 1 2 1 0 2 2 0 1 (1 ) (1 ) m m m em v e m v v m m m em v e m v v + − + + = + − + + = 完全非弹性碰撞: e=0,v2=v1 完全弹性碰撞: e=1, v2 -v1 = v10-v20 非完全弹性碰撞: 0<e<1
例题:如图所示,质量为1kg的钢球,系在 长为=0.8m的绳子的一端,绳子的另一端固 定。把绳子拉至水平位置后将球由静止释放, 球在最低点与质量为5kg的钢块作完全弹性碰 撞。求碰撞后钢球升高的高度。 解:本题分三个过程: 第一过程:钢球下落到最低点。以钢球和地球为系统,机械能 守恒。以钢球在最低点为重力势能零点。 ,w子=gl (1) 第二过程:钢球与钢块作完全弹性碰撞,! 以钢球和钢块为系 统,动能和动量守恒。 1 .21 1 -mv 0 n2 My2 (2) 2 2 mvo mv MV (3)
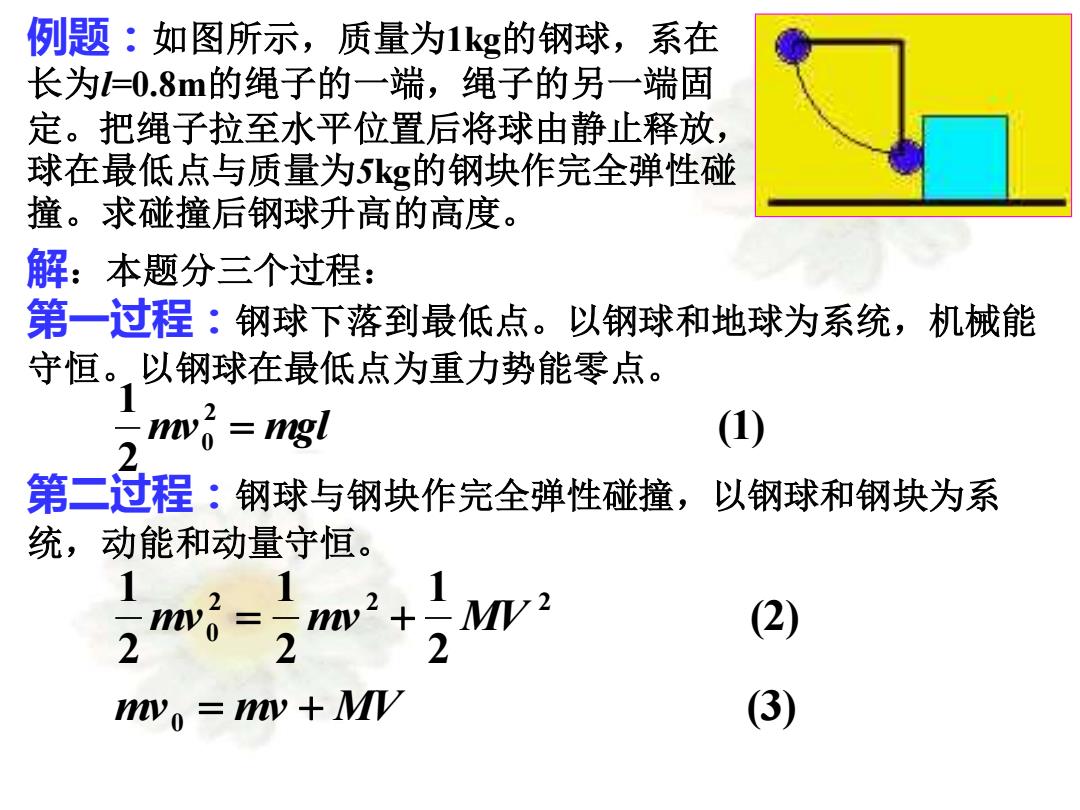
例题:如图所示,质量为1kg的钢球,系在 长为l=0.8m的绳子的一端,绳子的另一端固 定。把绳子拉至水平位置后将球由静止释放, 球在最低点与质量为5kg的钢块作完全弹性碰 撞。求碰撞后钢球升高的高度。 解:本题分三个过程: 第一过程:钢球下落到最低点。以钢球和地球为系统,机械能 守恒。以钢球在最低点为重力势能零点。 (1) 2 1 2 mv 0 = mgl 第二过程:钢球与钢块作完全弹性碰撞,以钢球和钢块为系 统,动能和动量守恒。 (3) (2) 2 1 2 1 2 1 0 2 2 2 0 mv mv MV mv mv MV = + = +