
海大理学院放学裸件 大学物理学电子教案 动量与动量守恒定律 3-1质点和质点系的动量守恒 3-2动量守恒定律 3-3系统内质量流动问题
3-1 质点和质点系的动量守恒 3-2 动量守恒定律 3-3 系统内质量流动问题 大学物理学电子教案 海大理学院教学课件 动量与动量守恒定律

复习 牛顿运动三定律 几种常见的力 万有引力、弹性力、摩擦力 惯性参考系力学相对性原理 牛顿运动定律成立的参考系称为惯性系 牛顿运动定律的应用 惯性力 f=-ma
复 习 牛顿运动三定律 几种常见的力 万有引力、弹性力、摩擦力 惯性参考系 力学相对性原理 牛顿运动定律成立的参考系称为惯性系 牛顿运动定律的应用 惯性力 f=-ma’

第三章 动量守恒定律和能量守恒定律 •牛顿第二定律 外力的作用,质点产生加速度,运动 状态发生变化。 •力的作用需要持续一段时间,或者需要持续一段距离, 这就是力对时间的累积作用和力对空间的累积作用。 ·质点或质点系的动量、动能或能量将发生变化或转移。 在一定条件下,质点系内的动量或能量将保持守恒
•牛顿第二定律——外力的作用,质点产生加速度,运动 状态发生变化。 •力的作用需要持续一段时间,或者需要持续一段距离, 这就是力对时间的累积作用和力对空间的累积作用。 •质点或质点系的动量、动能或能量将发生变化或转移。 在一定条件下,质点系内的动量或能量将保持守恒。 第三章 动量守恒定律和能量守恒定律
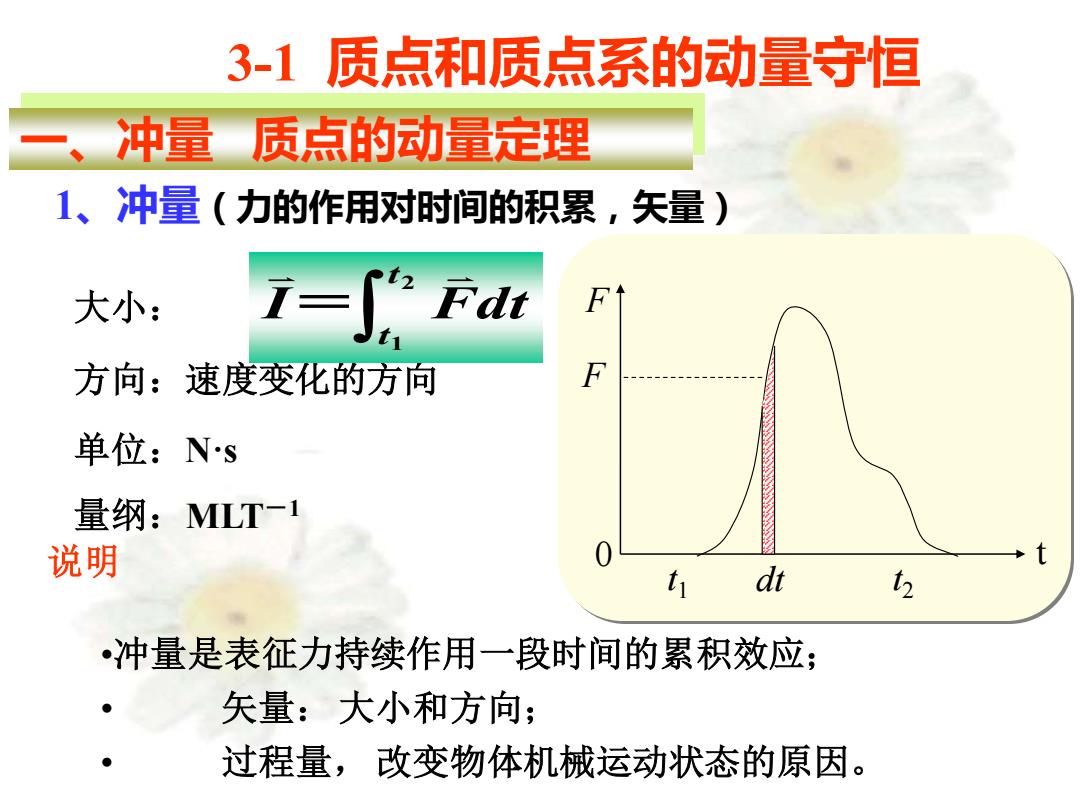
3-1」 质点和质点系的动量守恒 冲量质点的动量定理 1、冲量(力的作用对时间的积累,矢量) 大小: i=∫Fdt 方向:速度变化的方向 单位:Ns 量纲:MLT-1 说明 dt •冲量是表征力持续作用一段时间的累积效应; 矢量:大小和方向; ● 过程量,改变物体机械运动状态的原因
3-1 质点和质点系的动量守恒 一、冲量 质点的动量定理 1、冲量(力的作用对时间的积累,矢量) 大小: 方向:速度变化的方向 单位:N·s 量纲:MLT-1 说明 •冲量是表征力持续作用一段时间的累积效应; • 矢量: 大小和方向; • 过程量, 改变物体机械运动状态的原因。 2 1 t t I Fdt = t1 F 0 t t dt 2 F

2、动量 定义:物体的质量与速度的乘积叫做物体的动量 P=mv 动量是矢量,大小为w,方向就是速度的方向; 表征了物体的运动状态 单位:kgms1 量纲:MLT-1 牛顿第二定律的另外一种表示方法 d下d F=ma=m (mw)= dt dt dt
2、动量 定义:物体的质量与速度的乘积叫做物体的动量 P mv = •动量是矢量,大小为mv,方向就是速度的方向; • 表征了物体的运动状态 •单位: kg·m·s-1 •量纲:MLT-1 牛顿第二定律的另外一种表示方法 dt dP mv dt d dt dv F ma m = = = ( ) =

3、动量定理 dP Fdt dt ∫Rae=∫Fh 卫-p=i=∫Fdi F为恒力时,可以得出=F△t F作用时间很短时,可用力的平均值来代替。 7=∫Fd=△P I=F△t=△P 在给定的时间间隔内,外力作用在质点上的冲量,等于 该质点在此时间内动量的增量 一动量定理
3、动量定理 − = 2 1 2 1 t t P P I Fdt = F为恒力时,可以得出I=F t F作用时间很短时,可用力的平均值来代替。 I F t P I Fdt P = = = = 在给定的时间间隔内,外力作用在质点上的冲量,等于 该质点在此时间内动量的增量——动量定理 = 2 1 2 1 t t P P dP Fdt dP Fdt = dt dP F =
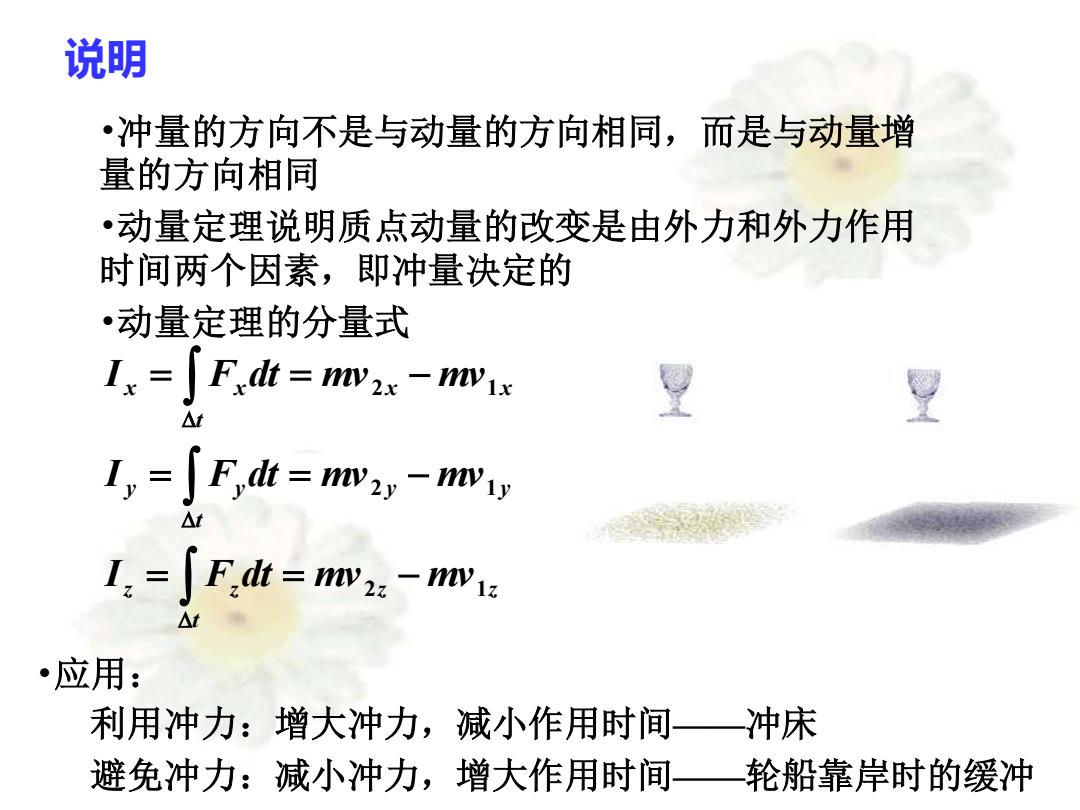
说明 •冲量的方向不是与动量的方向相同,而是与动量增 量的方向相同 •动量定理说明质点动量的改变是由外力和外力作用 时间两个因素,即冲量决定的 •动量定理的分量式 Is F,dt mvzx -mvx L,=了F,t=w2y-wy △t I2=∫F,dt=w2z-w1z △t •应用: 利用冲力:增大冲力,减小作用时间—冲床 避免冲力:减小冲力,增大作用时间 轮船靠岸时的缓冲
说明 •冲量的方向不是与动量的方向相同,而是与动量增 量的方向相同 •动量定理说明质点动量的改变是由外力和外力作用 时间两个因素,即冲量决定的 •动量定理的分量式 z z t z z y y t y y x x t x x I F dt mv mv I F dt mv mv I F dt mv mv 2 1 2 1 2 1 = = − = = − = = − •应用: 利用冲力:增大冲力,减小作用时间——冲床 避免冲力:减小冲力,增大作用时间——轮船靠岸时的缓冲

求作用力 t t 鸟本身的速度不快,质量也 不大,但相对于飞机来说,由于 i=∫Fd=△p 飞机速度很快,所以它们相互靠 近的速度很快。因此,鸟相对 飞机的速度很快,具有很大的相 △P 对动能,因此两者相撞时,会造 F= 成严重的空难事故 △t
求作用力 I Fdt P = = t P F =

例1、质量为2.5g的乒乓球以10m/s的速率 飞来,被板推挡后,又以20m/s的速率飞 出。设两速度在垂直于板面的同一平面内, 00 且它们与板面法线的夹角分别为45和30, 求:(1)乒乓球得到的冲量;(2)若撞 击时间为0.01s,求板施于球的平均冲力的 大小和方向。 解:取挡板和球为研究对象,由于作用 时间很短,忽略重力影响。设挡板对球 的冲力为F测有: T=∫F·t=,-m, 45 I.=∫Ft=w2cos30°-(-,)cos45FAt L,=F,t=w2sin30°-w1sin45°=F,△t
例1、质量为2.5g的乒乓球以10m/s的速率 飞来,被板推挡后,又以20m/s的速率飞 出。设两速度在垂直于板面的同一平面内, 且它们与板面法线的夹角分别为45o和30o , 求:(1)乒乓球得到的冲量;(2)若撞 击时间为0.01s,求板施于球的平均冲力的 大小和方向。 45o 30o n v2 v1 45o 30o n v2 v1 O x y 解:取挡板和球为研究对象,由于作用 时间很短,忽略重力影响。设挡板对球 的冲力为F则有: 2 1 I F dt mv mv = = − I F dt mv mv F t I F dt mv mv F t y y y x x x = = − = = = − − = sin30 sin45 cos 30 ( )cos45 2 1 2 1

△t=0.01sy1=10m/sy2=20ms m=2.5g F=6.1NF=0.7NF=VF+F=6.14N Ix=0.061NsI.=0.007Ns I=VT+I乃=6.14×10-2Ns ga=.=0.1148 0=6.54° o为I与x方向的夹角
t = 0.01s v1 = 10m/s v2 = 20m/s m = 2.5g 6.1N 0.7N 6.14N 2 2 Fx = Fy = F = F x + F y = 为 I 与x方向的夹角。 tg = = 0.1148 x y I I 6.14 10 Ns 2 2 −2 I = I x + I y = = 0.061N s = 0.007N s x y I I = 6.54