
一海大理学院表号裸件 大学物理学电子教案 电场强度与电势的关系 8一8电场场强与电势梯度 8一9静电场中的电偶极子电势
大学物理学电子教案 海大理学院教学课件 电场强度与电势的关系 8-8 电场场强与电势梯度 8-9 静电场中的电偶极子电势

复习 8-6静电场的环路定理 电势能 ·静电场力所作的功 ·静电场的环路定理 ·电势能 8-7电势 ·电势 。} 点电荷电场的电势 电势叠加原理
复 习 8-6 静电场的环路定理 电势能 • 静电场力所作的功 • 静电场的环路定理 • 电势能 8-7 电势 • 电势 • 点电荷电场的电势 • 电势叠加原理

8-8电场场强与电势梯度 等势面 1、 定义 疡中电势相等的点所构成的面,叫做等势 面。即V(xyz)=C,的空间曲面称为等势面。 等势面上的任一曲线叫做等势线。 2、等势面的性质 •在等势面上移动电荷时,电场力不作功; 除电场强度为零处外,电场线与等势面正交。 证明:因为将单位正电荷从等势面上M点移到N点, 电场力做功为零,而路径不为零,d≠0 dWv E.dI Edl cos=0 ..0=/2 •电场线的方向指向电势降落的方向
一、等势面 8-8 电场场强与电势梯度 1、定义 电场中电势相等的点所构成的面,叫做等势 面。即V(x,y,z)=C,的空间曲面称为等势面。 等势面上的任一曲线叫做等势线。 2、等势面的性质 •在等势面上移动电荷时,电场力不作功; l d M N E 证明:因为将单位正电荷从等势面上M点移到N点, 电场力做功为零,而路径不为零,dl≠0 dWMN = Edl = Edl cos = 0 = / 2 •除电场强度为零处外,电场线与等势面正交。 •电场线的方向指向电势降落的方向。 1 n 2 3
3、典型的电场线与等势面 正点电荷的电场 负点电荷的电场 匀强电 场 规定:两个相邻等势面的电势差相等,所以等势面较密 集的地方,场强较大;等势面较稀疏的地方,场强较小。 4、应用 测量电势分布,得到等势面,在根据等势面与电场 强度的关系,定性画出电场线
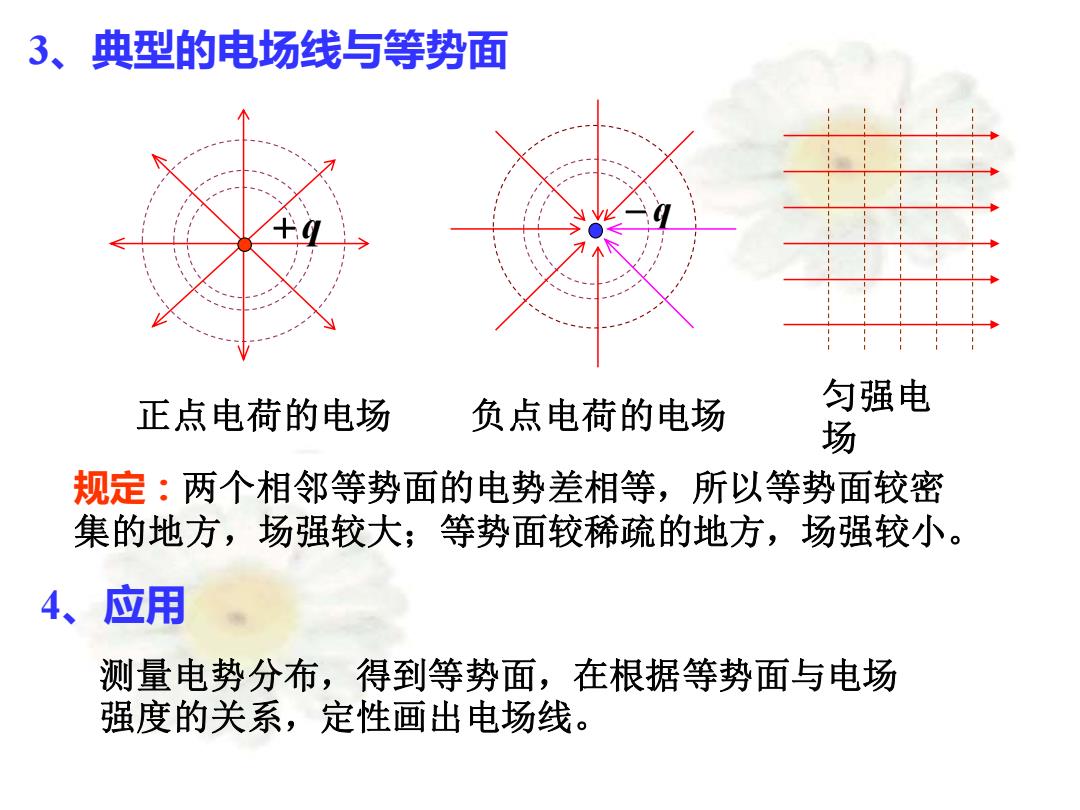
3、典型的电场线与等势面 + q − q 正点电荷的电场 负点电荷的电场 匀强电 场 规定:两个相邻等势面的电势差相等,所以等势面较密 集的地方,场强较大;等势面较稀疏的地方,场强较小。 4、应用 测量电势分布,得到等势面,在根据等势面与电场 强度的关系,定性画出电场线
二、 电场强度与电势的关系 1、沿任一方向的分量 V+△V 静电场中两个靠得很近的等势面,电势分 别为V和4△V,在等势面上取两点A和B, B 间距为△1,设与E之间的夹角为0。 V,-V3=E·△M=E.△1.cos0 -△V=E,△l 负号表明:沿着场强的方向,电势 △V 由高到低;逆着场强的方向,电势 E=- △M 由低到高 △ E=-lim △→0 dl 电场中某一点的场强沿任一方向的分量,等于这一点的电 势沿该方向单位长度的电势变化率的负值,这就是电场强 度和电势之间的关系
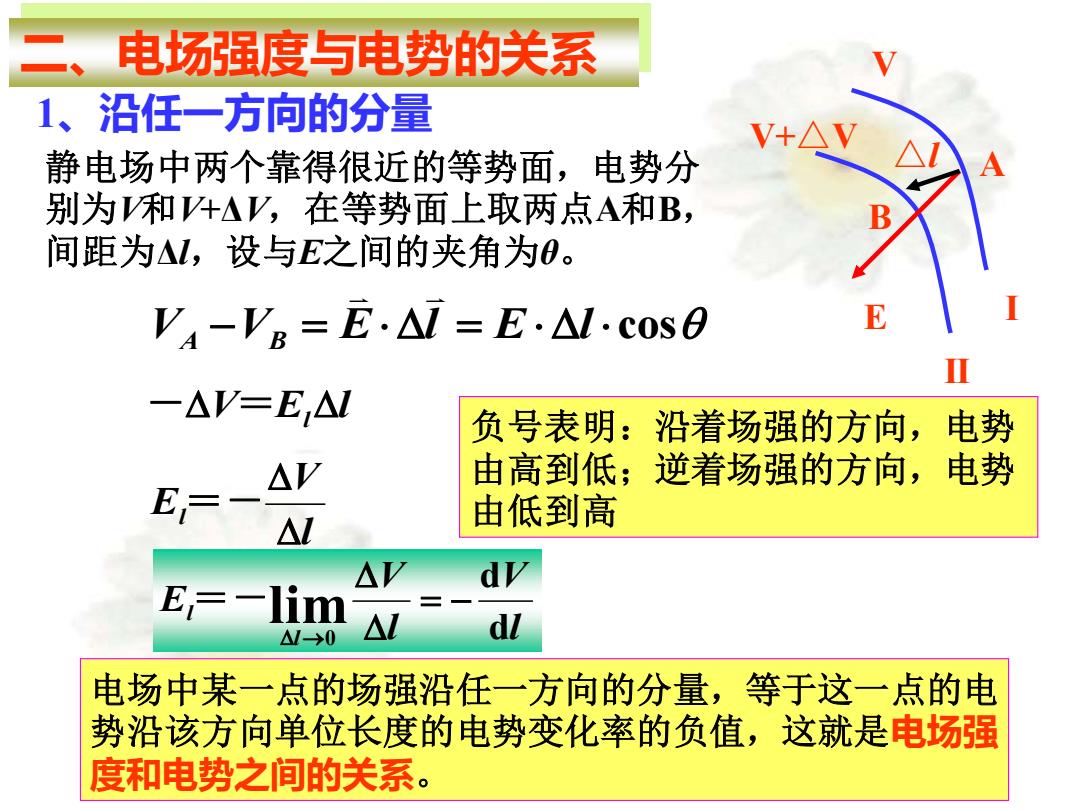
二、电场强度与电势的关系 1、沿任一方向的分量 B A I II E △l V V+△V 静电场中两个靠得很近的等势面,电势分 别为V和V+ΔV,在等势面上取两点A和B, 间距为Δl,设与E之间的夹角为θ。 VA −VB = El = El cos V E l - = l l V El =- 负号表明:沿着场强的方向,电势 由高到低;逆着场强的方向,电势 由低到高 l V l V E l l d d lim 0 = − → = - 电场中某一点的场强沿任一方向的分量,等于这一点的电 势沿该方向单位长度的电势变化率的负值,这就是电场强 度和电势之间的关系
2、1 切向和法向分量 等势面上任一点场强的切向分量为零 •法向分量 dV 电场中任一点的场强, dl 等于该点电势沿等势 低电势 面法线方向单位长度 高电势 E=一 dl, 的变化率的负值。 dr 3、 应用 E e=-VV=-gradv dn 电势是标量,容易计算。 直角坐标系E= Ov+ 可以先计算电势,然后利 用场强与电势的微分关系 计算电场强度,这样做的 av E.= E,=- ov E,= av 好处是可以避免直接用场 Ox y 8x 强叠加原理计算电场强度 的矢量运算的麻烦
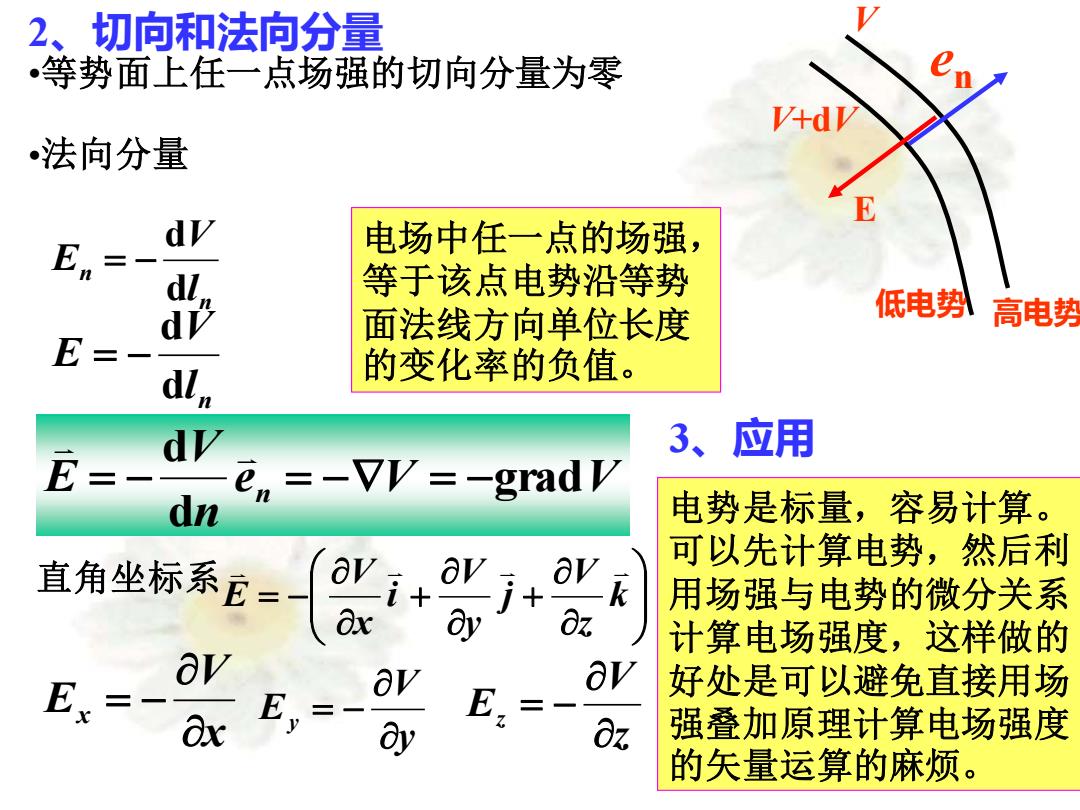
2、切向和法向分量 •等势面上任一点场强的切向分量为零 •法向分量 n n l V E d d = − n l V E d d = − e V V n V E n grad d d = − = − = − 电场中任一点的场强, 等于该点电势沿等势 面法线方向单位长度 的变化率的负值。 V V+dV E en 低电势 高电势 直角坐标系 + + = − k z V j y V i x V E x V Ex = − y V Ey = − z V Ez = − 3、应用 电势是标量,容易计算。 可以先计算电势,然后利 用场强与电势的微分关系 计算电场强度,这样做的 好处是可以避免直接用场 强叠加原理计算电场强度 的矢量运算的麻烦
例题1,求均匀带电细圆环轴线上一点的场强。 解:细圆环轴线上一点的电势为 4π(x2+R2rP 式中R为圆环的半径。因而轴线上一 点的场强为 dg E=- av a X Ox x4z6c2+R2Ψ4r6(c2+R2 E,=0 E,=0
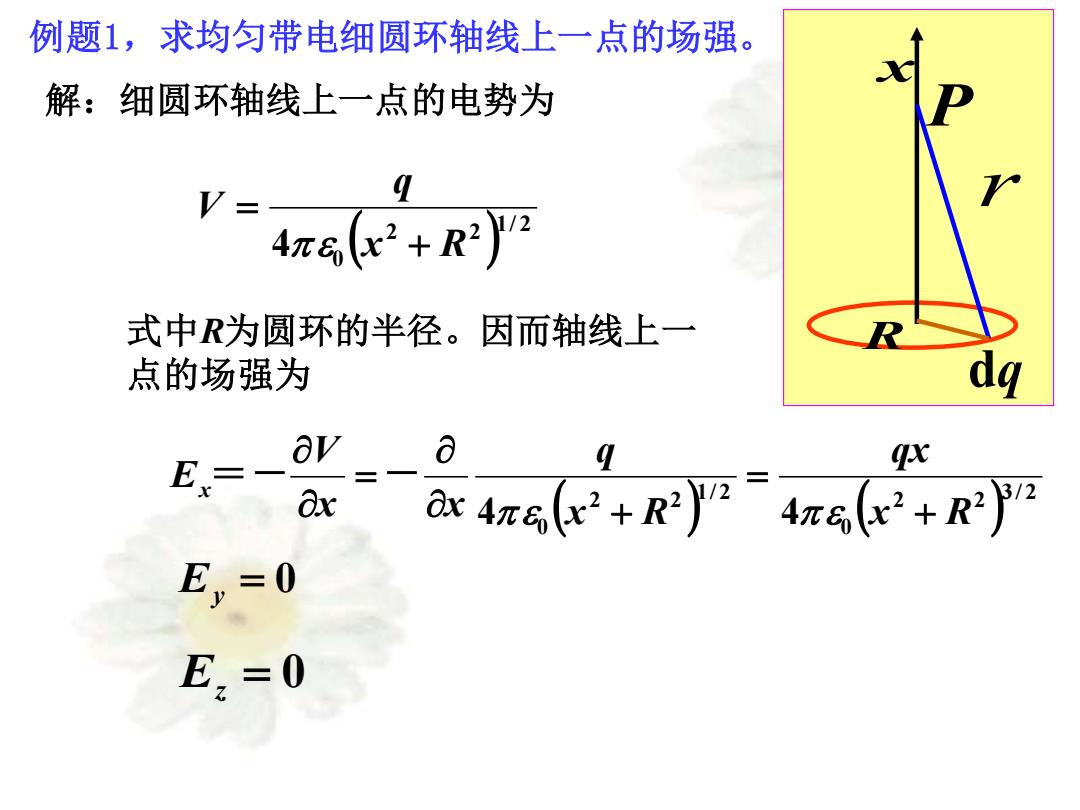
例题1,求均匀带电细圆环轴线上一点的场强。 解:细圆环轴线上一点的电势为 ( ) 1/ 2 2 2 4 0 x R q V + = 式中R为圆环的半径。因而轴线上一 点的场强为 ( ) ( ) 3/ 2 2 2 0 1/ 2 2 2 4 0 4 x R qx x R q x x V Ex + = + = = - - Ey = 0 Ez = 0 x R r P dq

例题2,求电偶极子电场中任一点的电势和电场强度。 解:设A与+g和-g均在xoy平面内,A到+q和-q 的距离分别为r,和r,+q和-q单独存在时,A 点的电势为 V+= q y= q 4πr+ 4πr- 由电势的叠加原理,A点的电势为 V=V+M=,4 4π6 对于电偶极子,1<<r,所以 r-r=Icos0 rr=r2V= q Icose 电场强度为 4π6 引入电偶极子的偶极矩p=ql av y2-2x2 Ex=一 Ex V= 4r6(e2+y25 4xar2r 4xa (x2+y2) ov -3xV = Oy 4π (x2+y252
例题2,求电偶极子电场中任一点的电势和电场强度。 − r − q 0 r + q + r r A x 解:设A与+q和-q均在xoy平面内,A到+q和-q y 的距离分别为r+和r-,+q和-q单独存在时,A 点的电势为 + r q V 4 0 + = - - = r q V 4 0 由电势的叠加原理,A点的电势为 − = = + − + − − + + − − r r q r r r r q V V V 0 4 0 1 1 4 + = 对于电偶极子,l <<r,所以 2 r − r = l cos r r = r − + + − 2 0 cos 4 r q l V = 引入电偶极子的偶极矩p=ql ( ) 3/ 2 2 2 0 2 0 4 4 x y p x r x r p V + = = 电场强度为 ( ) 5/ 2 2 2 2 2 0 2 4 x y p y x x V Ex + − = − = − ( ) 5/ 2 2 2 0 3 4 x y p xy y V Ey + − = − = −

ov Ex= y2-2x2 ax 4r6(c2+y25 av -3y 4r2+y2 电偶极子的延长线上y=0 2p1 Ex= 4π6x3 E,=0 电偶极子的中垂线上x=0 E=- 1 4π6y3 E,=0
-q +q -q +q 电偶极子的延长线上 y = 0 3 0 1 4 2 x p Ex = Ey = 0 电偶极子的中垂线上 x = 0 3 0 1 4 y p Ex = − Ey = 0 ( ) 5/ 2 2 2 2 2 0 2 4 x y p y x x V Ex + − = − = − ( ) 5/ 2 2 2 0 3 4 x y p xy y V Ey + − = − = −

8-9 静电场中的电偶极子 在外电场中电偶极子的力矩和取向 1、在匀强电场中的受力情况 F.=gE E=-dE F=F+十F=qE-qE=0 在匀强电场中,电偶极子不受电场力的作用;电偶极子 没有平动。 2、在匀强电场中所受的力矩 M=grEsine=pE sin M=p×E 在力矩的作用下,电偶极子将在平面内转动
8-9 静电场中的电偶极子 一、在外电场中电偶极子的力矩和取向 1、在匀强电场中的受力情况 F qE + = F qE − =− F F F qE − qE = 0 = + + - = 在匀强电场中,电偶极子不受电场力的作用;电偶极子 没有平动。 -q +q F+ F- θ r0 2、在匀强电场中所受的力矩 M = q r0 Esin = pEsin M p E = 在力矩的作用下,电偶极子将在平面内转动