
海大理学院教学裸件 大学物理学电子教案 单摆和复摆、简谐运动的能量 14-4单摆与复摆 14-5简谐运动的能量
大学物理学电子教案 海大理学院教学课件 单摆和复摆、简谐运动的能量 14-4 单摆与复摆 14-5 简谐运动的能量
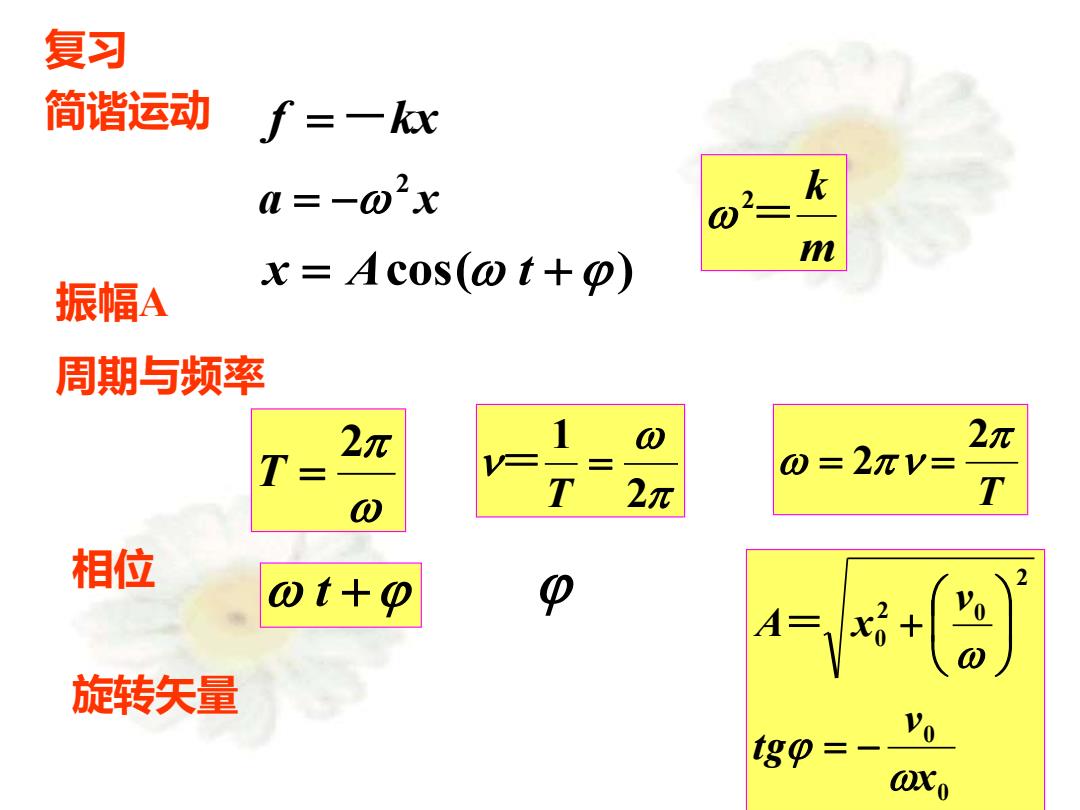
复习 简谐运动 f=一x a=-02x x=Acos(@t+o) m 振幅A 周期与频率 2 元 2元 0=2πV= 2元 T 相位 t+p 旋转矢量 tgo=- @xo
复习 简谐运动 f =-kx a x 2 = − x = Acos( t +) 振幅A 周期与频率 2 T = 2 1 = T = T 2 = 2 = 相位 t + 0 0 2 2 0 0 x v tg v A x = − = + m k 2 = 旋转矢量

14-4单摆与复摆 实际发生的振动比较复杂;例如 回复力不一定是弹性力—而是重力,浮力等其它性 质的力; 合外力可能是非线性力一只有在一定的条件下,才 能近似当作线性回复力。 研究问题的一般方法: 根据问题的性质,突出主要因素,建立合理的物理模 型,使计算简化。 本节讨论两个实际振动问题的近似处理:单摆与复摆
14-4 单摆与复摆 实际发生的振动比较复杂;例如 •回复力不一定是弹性力——而是重力,浮力等其它性 质的力; •合外力可能是非线性力——只有在一定的条件下,才 能近似当作线性回复力。 研究问题的一般方法: 根据问题的性质,突出主要因素,建立合理的物理模 型,使计算简化。 本节讨论两个实际振动问题的近似处理:单摆与复摆
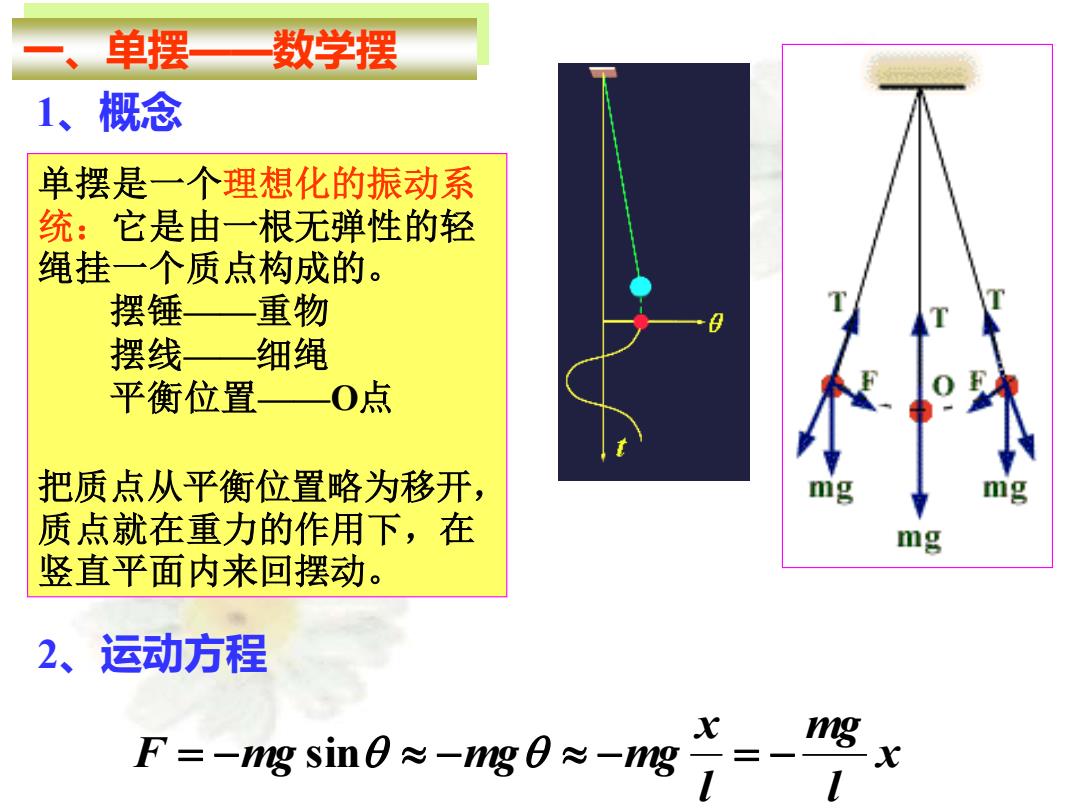
一、 单摆 数学摆 1、概念 单摆是一个理想化的振动系 统:它是由一根无弹性的轻 绳挂一个质点构成的。 摆锤一重物 摆线一细绳 平衡位置—0点 把质点从平衡位置略为移开, mg mg 质点就在重力的作用下,在 mg 竖直平面内来回摆动。 2、运动方程 火 F=-mg sin0≈-gB≈-g g 子
一、单摆——数学摆 1、概念 单摆是一个理想化的振动系 统:它是由一根无弹性的轻 绳挂一个质点构成的。 摆锤——重物 摆线——细绳 平衡位置——O点 把质点从平衡位置略为移开, 质点就在重力的作用下,在 竖直平面内来回摆动。 2、运动方程 x l mg l x F = −mg sin −mg −mg = −
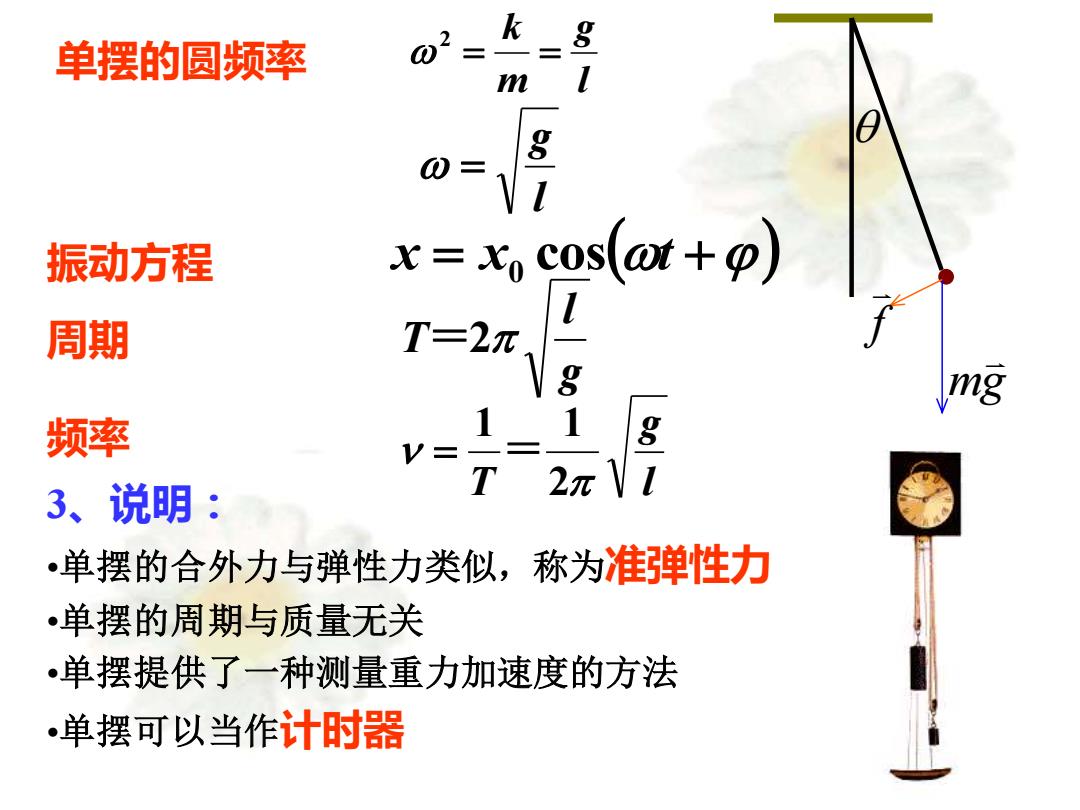
单摆的圆频率 2= @-\1 振动方程 x=cos(ot+p) 周期 T=2元 mg 频率 1 1 8 V= T 3、说明: 2π •单摆的合外力与弹性力类似,称为准弹性力 •单摆的周期与质量无关 •单摆提供了一种测量重力加速度的方法 •单摆可以当作计时器
单摆的圆频率 l g m k = = 2 振动方程 x = x cos(t +) 0 周期 g l T=2 频率 l g T 2 1 1 = = l g = 3、说明: •单摆的合外力与弹性力类似,称为准弹性力 •单摆的周期与质量无关 •单摆提供了一种测量重力加速度的方法 •单摆可以当作计时器 mg f
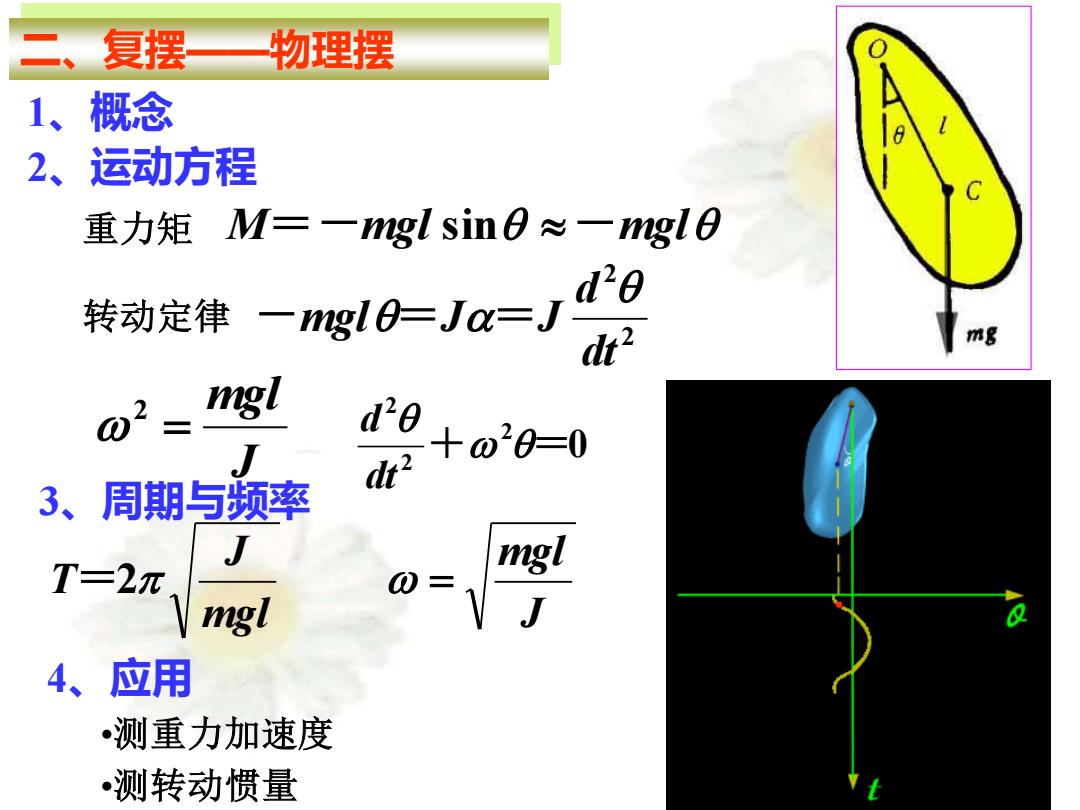
二、复摆 物理摆 1、概念 2、运动方程 重力矩M=-ngl sin0≈一nglB d20 转动定律一mgl0=Ja=J dr mg 02 mgl +oa=0 d20 3、周期与频率 J T=2π mgl 0=, mgl 4、 应用 •测重力加速度 •测转动惯量
二、复摆——物理摆 1、概念 2、运动方程 重力矩 M= -mgl sin -mgl 转动定律 2 2 dt d mgl J J - = = J mgl = 2 0 2 2 2 + = dt d 3、周期与频率 J mgl mgl J T=2 = 4、应用 •测重力加速度 •测转动惯量

14-5 简谐运动的能量 简谐运动的能量 m 以弹簧振子为例 ”多 x=Acos(at+o) y=-A@sin(at+o) E=2m1o2=k 系统动能 Es-1m2-1mA@'sin'(@x+@) 系统势能 E。=,x2=k4cos2(ot+p) 2 系统的总能量 1 E-Ex+E=mA'@'sin'(@x+p)+kAcos(@x+p) 2 弹簧振子作简谐运动的能量与振幅的平方成正比
14-5 简谐运动的能量 一、简谐运动的能量 以弹簧振子为例 k m o x X ( ) ( ) = − + = + v A t x A t sin cos 系统动能 E = mv = mA (t +) k 2 2 2 2 sin 2 1 2 1 系统势能 E = kx kA ( t +) p cos 2 1 2 1 2 = 2 2 系统的总能量 E E E = mA (t +) kA (t +) k p 2 2 2 2 2 cos 2 1 sin 2 1 = + + 2 2 2 2 1 2 1 E= mA = kA 弹簧振子作简谐运动的能量与振幅的平方成正比

二、 能量平均值 1、 动能的时间平均值 豆-f5m4asna+pw=mo=4 2、势能的时间平均值 7了及4cos6as+ph-k4-m4o 结论 简谐运动的动能与势能在一个周期内的平均值相 等,它们都等于总能量的一半
二、能量平均值 1、动能的时间平均值 ( ) 2 2 2 0 2 2 2 4 1 4 1 sin 2 1 1 mA t dt mA kA T E T k = + = = 2、势能的时间平均值 ( ) + = = T p kA t dt kA mA T E 0 2 2 2 2 2 4 1 4 1 cos 2 1 1 = 简谐运动的动能与势能在一个周期内的平均值相 等,它们都等于总能量的一半。 结论

三、应用 忽略阻力,机械能守恒,作简谐运动的 dx m.v +k·xy=0 系统只有动能和势能,有 e+E小0 dx k dt2 =0 n 将具体问题中的动能与势能表达式代入 上式,可得到简谐运动的微分方程及振 令 动周期和频率。 例题、用机械能守恒定律求弹簧振子的 运动方程。 解:弹簧振子在振动过程中,机械能守恒 日w+=C +02x=0 2 两边对时间求导, 1 2x=0 k.2x x=Acos(ax+o 2m2v
三、应用 忽略阻力,机械能守恒,作简谐运动的 系统只有动能和势能,有 (Ek + Ep )= 0 dt d 将具体问题中的动能与势能表达式代入 上式,可得到简谐运动的微分方程及振 动周期和频率。 例题、用机械能守恒定律求弹簧振子的 运动方程。 解:弹簧振子在振动过程中,机械能守恒 mv + kx = kA = C 2 2 2 2 1 2 1 2 1 2 0 2 1 2 2 1 + = dt dx k x dt dv m v 两边对时间求导,得 0 2 2 + k xv = dt d x m v 0 2 2 + x = m k dt d x m k 2 = 0 2 2 2 + x = dt d x x = Acos(t +) 令

小结 单摆和复摆 简谐运动的能量 5-mto 2
小 结 单摆和复摆 简谐运动的能量 2 2 2 2 1 2 1 E= mA = kA