
海大理学院敖学裸件 大学物理学电子教案 光的衍射(1) 17-6光的衍射 17-7单缝夫衍射
大学物理学电子教案 海大理学院教学课件 光的衍射(1) 17-6 光的衍射 17-7 单缝夫衍射

复习 光程 薄膜干涉 ·劈尖牛顿环 ·迈克耳孙干涉仪
复 习 • 光程 薄膜干涉 • 劈尖 牛顿环 • 迈克耳孙干涉仪
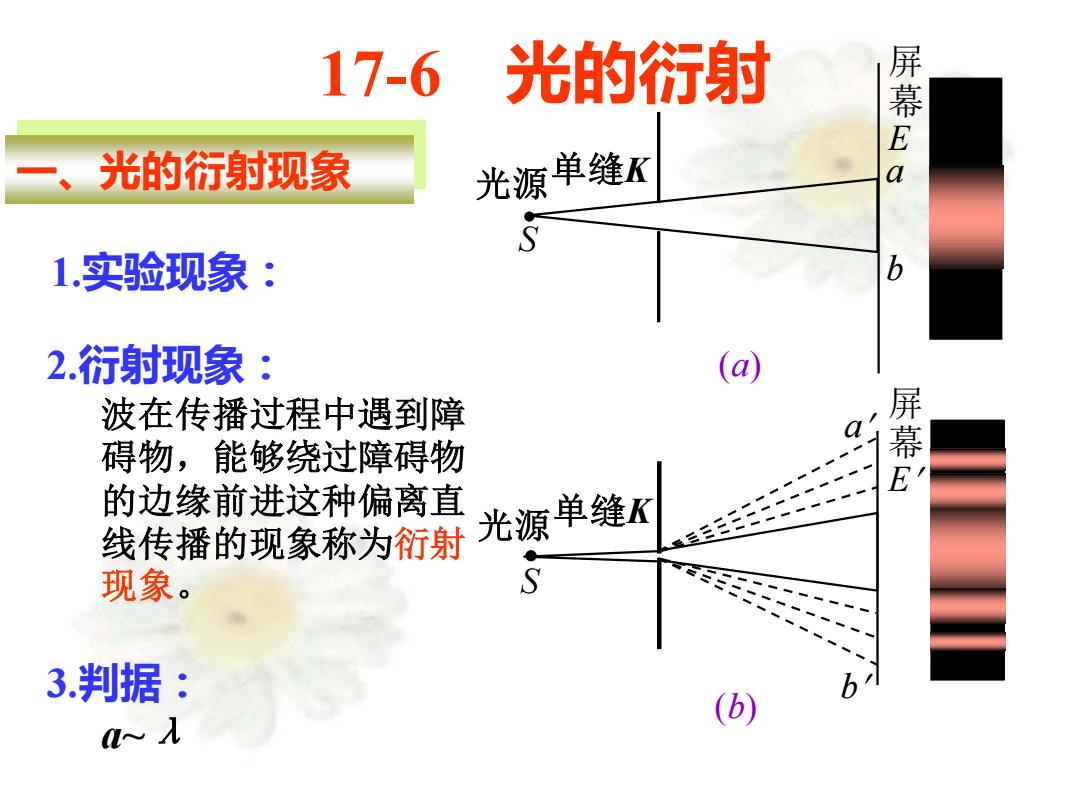
17-6 光的衍射 光的衍射现象 光源单缝K 屏幕EC 1.实验现象: b 2.衍射现象: (a) 波在传播过程中遇到障 a 碍物,能够绕过障碍物 幕 的边缘前进这种偏离直 线传播的现象称为衍射 光源单缝K 现象。 3判据: 6」 (b) a~入
17-6 光的衍射 一、光的衍射现象 2.衍射现象: 波在传播过程中遇到障 碍物,能够绕过障碍物 的边缘前进这种偏离直 线传播的现象称为衍射 现象。 3.判据: a~λ 1.实验现象: 单缝K a b S 光源 (a) 屏 幕 E 屏 幕 E 单缝K a S 光源 (b) b
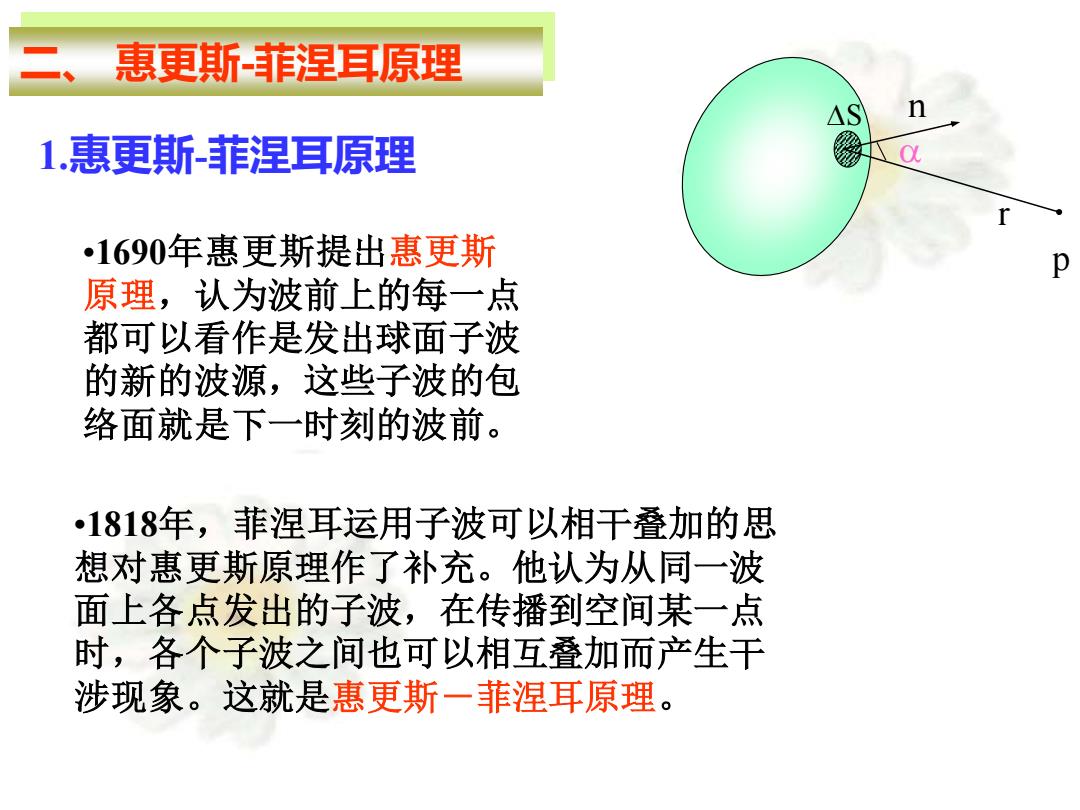
惠更斯菲涅耳原理 △S n 1惠更斯-菲涅耳原理 1690年惠更斯提出惠更斯 p 原理,认为波前上的每一点 都可以看作是发出球面子波 的新的波源,这些子波的包 络面就是下一时刻的波前。 1818年,菲涅耳运用子波可以相干叠加的思 想对惠更斯原理作了补充。他认为从同一波 面上各点发出的子波,在传播到空间某一点 时,各个子波之间也可以相互叠加而产生干 涉现象。这就是惠更斯一菲涅耳原理
二、 惠更斯-菲涅耳原理 •1690年惠更斯提出惠更斯 原理,认为波前上的每一点 都可以看作是发出球面子波 的新的波源,这些子波的包 络面就是下一时刻的波前。 •1818年,菲涅耳运用子波可以相干叠加的思 想对惠更斯原理作了补充。他认为从同一波 面上各点发出的子波,在传播到空间某一点 时,各个子波之间也可以相互叠加而产生干 涉现象。这就是惠更斯-菲涅耳原理。 1.惠更斯-菲涅耳原理 S p r n

2.惠更斯-菲涅耳原理的数学表达式 △S n E(p)C.Fms dS p 菲涅耳衍射积分公式: (cF(owl 对于点光源发出的球面波,初相位可取为零,且倾斜因子 1+cose F(0)= 说明 2 菲涅耳积分可以计算任意 形状波的阵面衍射问题。 它说明子波为什么不会向后退。 •采用半波带法来定性地解 释衍射现象
说明 •菲涅耳积分可以计算任意 形状波的阵面衍射问题。 •采用半波带法来定性地解 释衍射现象。 2.惠更斯-菲涅耳原理的数学表达式 r dS dS r dE p C F t ( )] 2 ( ) ( )cos[ 0 = − + = = − + S S r dS dS r E p dE p C F t ( )] 2 ( ) ( ) ( )cos[ 0 菲涅耳衍射积分公式: 对于点光源发出的球面波,初相位可取为零,且倾斜因子 2 1 cos ( ) + F = 它说明子波为什么不会向后退。 S p r n
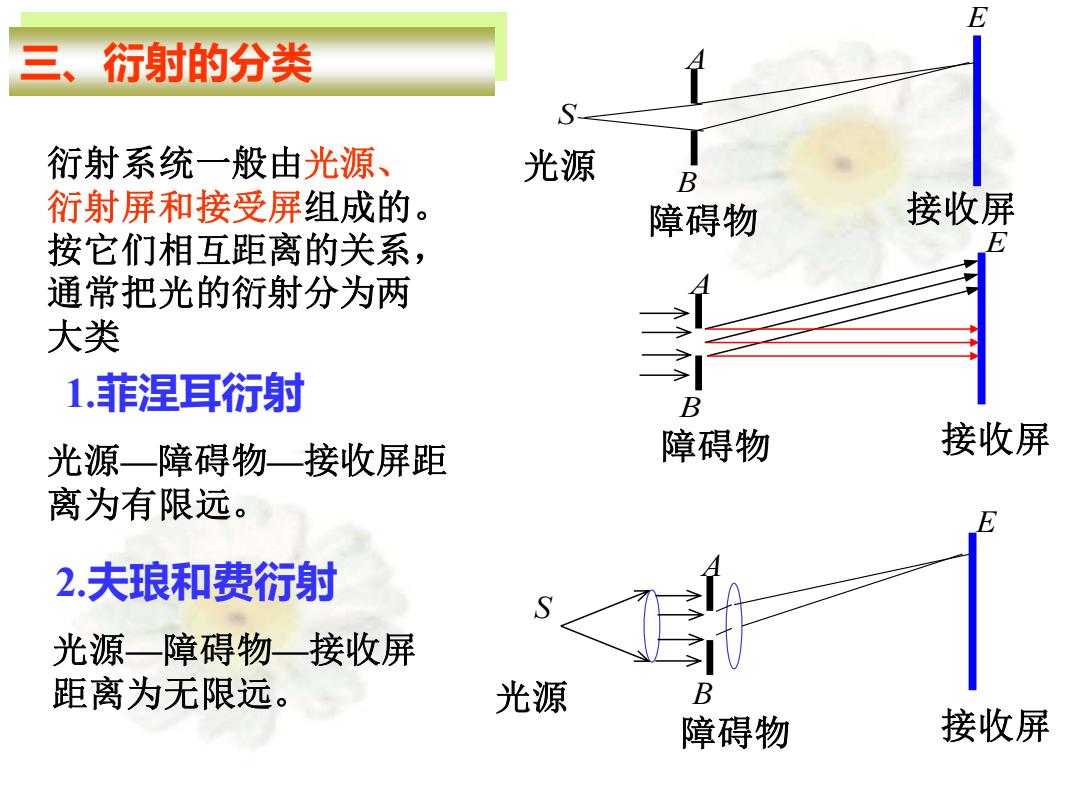
三、衍射的分类 S 衍射系统一般由光源、 光源 B 衍射屏和接受屏组成的。 障碍物 接收屏 按它们相互距离的关系, E 通常把光的衍射分为两 大类 1.菲涅耳衍射 B 光源一障碍物一接收屏距 障碍物 接收屏 离为有限远。 2.夫琅和费衍射 光源一障碍物—接收屏 距离为无限远。 光源 B 障碍物 接收屏
S A B E 光源 障碍物 接收屏 S A B E 光源 障碍物 接收屏 三、衍射的分类 1.菲涅耳衍射 2.夫琅和费衍射 光源—障碍物—接收屏距 离为有限远。 光源—障碍物—接收屏 距离为无限远。 A B E 障碍物 接收屏 衍射系统一般由光源、 衍射屏和接受屏组成的。 按它们相互距离的关系, 通常把光的衍射分为两 大类
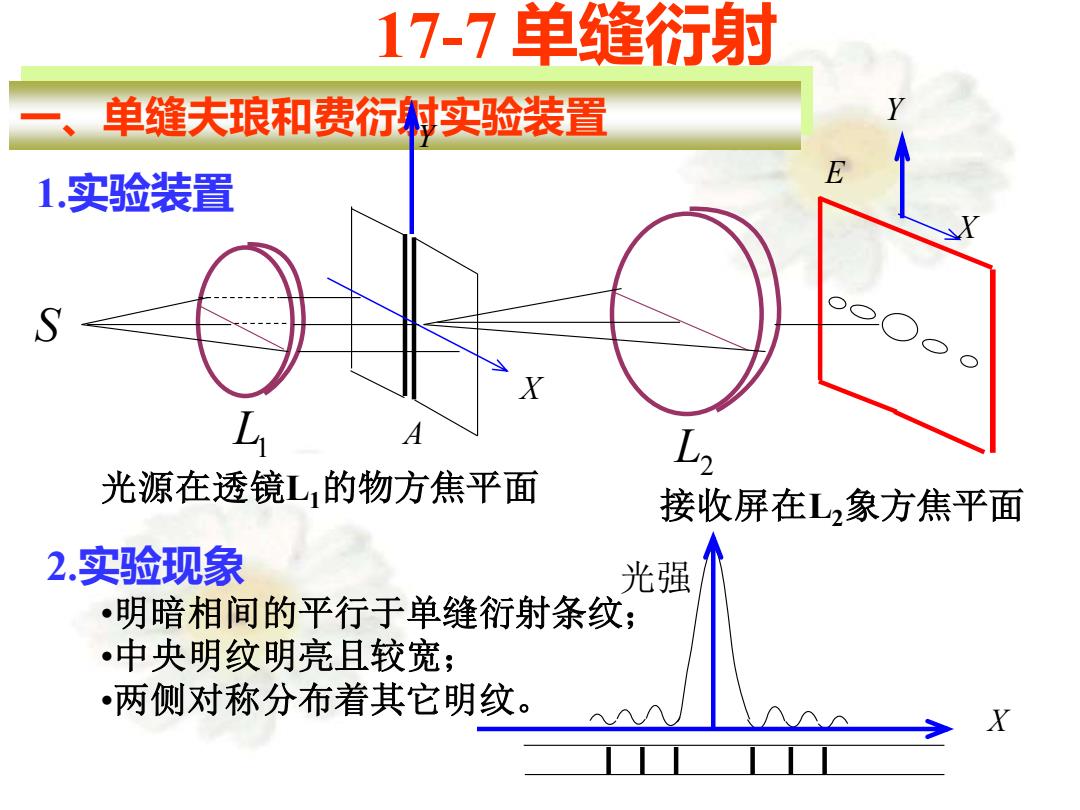
17-7单缝行射 单缝夫琅和费衍村实验装置 1.实验装置 L A 光源在透镜L,的物方焦平面 接收屏在L,象方焦平面 2.实验现象 光强 •明暗相间的平行于单缝衍射条纹 中央明纹明亮且较宽; •两侧对称分布着其它明纹。 X
17-7 单缝衍射 光源在透镜L1的物方焦平面 接收屏在L2象方焦平面 X 光强 一、单缝夫琅和费衍射实验装置 S L1 A L2 E Y Y X X 1.实验装置 2.实验现象 •明暗相间的平行于单缝衍射条纹; •中央明纹明亮且较宽; •两侧对称分布着其它明纹
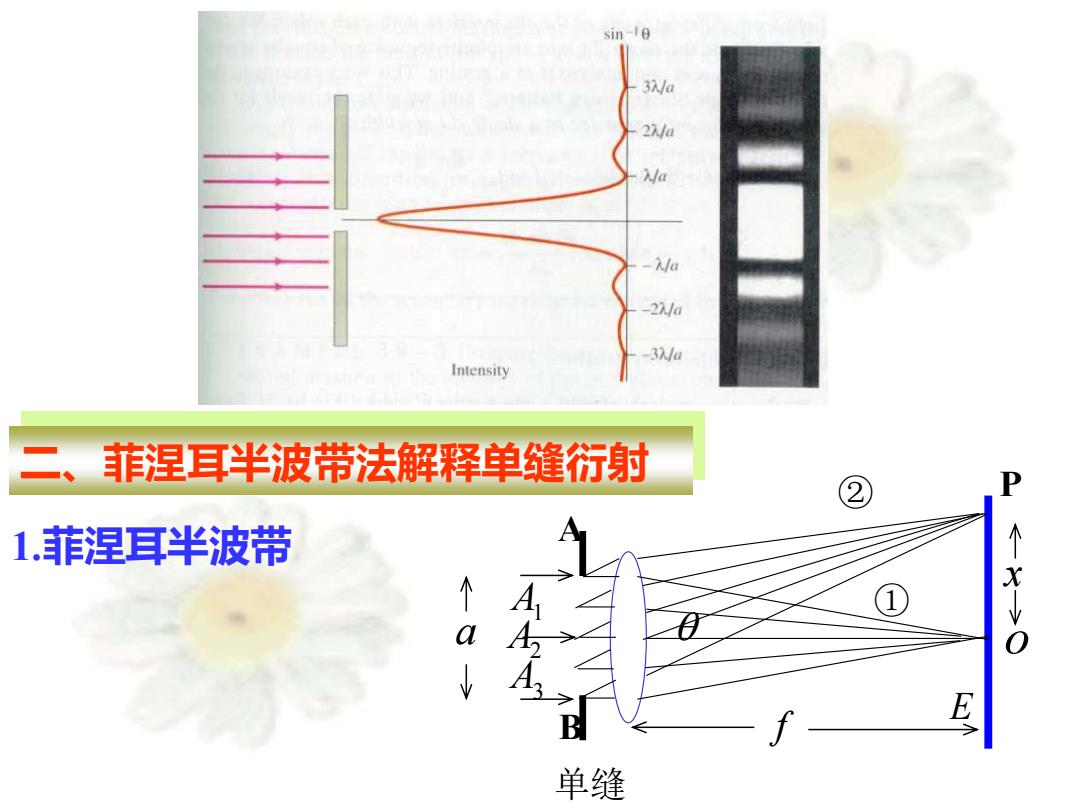
sin-10 3/ 2/ -/a 2/a 3/a Intensity 二、菲涅耳半波带法解释单缝衍射 ② D 1.菲涅耳半波带 B 单缝
二、菲涅耳半波带法解释单缝衍射 1.菲涅耳半波带 E 单缝 f x o A3 A1 A2 a ① ② P B A

半波带的作法: A,B两条平行光线之间的光程差 BC=asin0. 作平行于AC的平面,使相邻平面 之间的距离等于入射光的半波长, (位相差π) 如图把AB波阵面分成AA1,A1A2, A 0 A2B波带. 两相邻波带对应点AA,中A和 AA2中A2,到达P点位相差为π, 光程差为入2。这样的波带就 是菲涅耳半波带。 B 222g asinΦ 所以任何两个相邻波带所发出的光线在 P点相互抵消. 当BC是)2的偶数倍,所有波带成对抵消,P点暗, 当BC是入/2的奇数倍,所有波带成对抵消后留下一个波带,P点明
半波带的作法: A B a θ A,B两条平行光线之间的光程差 BC=asinθ. θ 作平行于AC的平面,使相邻平面 之间的距离等于入射光的半波长. (位相差) 如图把AB波阵面分成AA1,A1A2, A2B波带. 2 λ 2 λ 2 λ A1 A2 两相邻波带对应点AA1中A1和 AA2中A2,到达P点位相差为, 光程差为/2。这样的波带就 是菲涅耳半波带。 所以任何两个相邻波带所发出的光线在 P点相互抵消. 当BC是/2的偶数倍,所有波带成对抵消,P点暗, 当BC是/2的奇数倍,所有波带成对抵消后留下一个波带,P点明

2.特点:将波面分成整数个波带,各波带面积 相等,相邻波带的相位差为元,则: asine=2kA/2 暗纹中心 k=士1,±2. asin0=(2k+1)2/2 明纹中心
2.特点:将波面分成整数个波带,各波带面积 相等,相邻波带的相位差为 ,则: asin = 2k / 2 a sin = (2k + 1) / 2 暗纹中心 明纹中心 k = 1,2