
一海大理学院教学裸件 大学物理学电子教索 量子物理(5) 19-9 氢原子的量子理论简介 ·氢原子的定态薛定谔方程 三个量子数 。1 氢原子在基态时的径向波函 数和电子的分布概率 19-10多电子原子中的电子分布 ·电子自旋自旋磁量子数 ·四个量子数 多电子原子中的由子分布
大学物理学电子教案 海大理学院教学课件 量子物理(5) 19-9 氢原子的量子理论简介 • 氢原子的定态薛定谔方程 • 三个量子数 • 氢原子在基态时的径向波函 数和电子的分布概率 19-10 多电子原子中的电子分布 • 电子自旋 自旋磁量子数 • 四个量子数 • 多电子原子中的电子分布

复习 波函数概率密度 薛定谔方程 ● 一维势阱问题 对应原理 ,一维方势垒隧道效应
复 习 • 波函数 概率密度 • 薛定谔方程 • 一维势阱问题 • 对应原理 • 一维方势垒 隧道效应

19-9 氢原子的量子理论简介 •氢原子是最简单的原子,核外只有一个电子绕核运动。 量子力学对氢原子问题有完满的论述,但是数学运算仍 十分复杂,超过了大学物理的教学要求。 •量子力学能够给出原子系统中电子状态的描述并且自然 地得出量子化的结果。 •通过对氢原子量子特性的讨论,能使我们对原子世界有 一个较为清晰的图象
19-9 氢原子的量子理论简介 •氢原子是最简单的原子,核外只有一个电子绕核运动。 量子力学对氢原子问题有完满的论述,但是数学运算仍 十分复杂,超过了大学物理的教学要求。 •量子力学能够给出原子系统中电子状态的描述并且自然 地得出量子化的结果。 •通过对氢原子量子特性的讨论,能使我们对原子世界有 一个较为清晰的图象

氢原子的定态薛定谔方程 设氢原子中电子的质量为m,电荷为-e,它与原子核之 间的距离为。取原子核为原点O,则电子的势能为 e Ep=- 4πr 定态薛定鄂方程为 ΨG)=E平) 2m 4πr V)+ 8π2m e2 E+ h2 Ψ)=0 4π8 在球坐标系下 x =rsinecoso y=rsinθsinp =rcose X
一、氢原子的定态薛定谔方程 设氢原子中电子的质量为m,电荷为-e,它与原子核之 间的距离为r。取原子核为原点O,则电子的势能为 r e EP 0 2 4 = − 定态薛定鄂方程为 (r) E (r) r e m = − − 0 2 2 2 2 4 ( ) ( ) 0 4 8 0 2 2 2 2 = + + r r e E h m r 在球坐标系下 z y x x = rsin cos y = rsin sin z = r cos

定态薛定鄂方程为 1∂2Ψ 00)r2 sin20 002 分离变量 (F)=R(ro(e() 1d2Φ =mi Φdp2 d do sine =10+1) sin20 ⊙sin0d0 do l d ,2 dR 8π2nm2 e2 E+ R dr dr h =0+1) 4πI
定态薛定鄂方程为 0 4 8 sin 1 sin sin 1 1 0 2 2 2 2 2 2 2 2 2 2 = + + + + r e E h m r r r r r r 分离变量 (r) = R(r)( )() 2 2 2 1 ml d d = − sin ( 1) sin 1 sin2 2 = + − l l d d d ml d ( 1) 4 1 8 0 2 2 2 2 2 = + + + l l r e E h mr dr dR r dr d R
二、三个量子数 1、能量量子化与主量子数 求解氢原子波函数的径向方程,根据波函数满足单值、有限 和连续的条件,可得氢原子的能量是量子化的 me 1 E (4πa}2h2n2 n=1,2,3, me =13.6eV (4π6}2h2 念 13.6 E=- e n=1,2,3,… E 讨论: •由解薛定鄂方程得到的能量公式与波耳理论的结果相同, 氢原子的能量只能取分立值,即能量是量子化的。称为主 量子数; =1的能级称为基态能级,>1的能级称为激发态能级
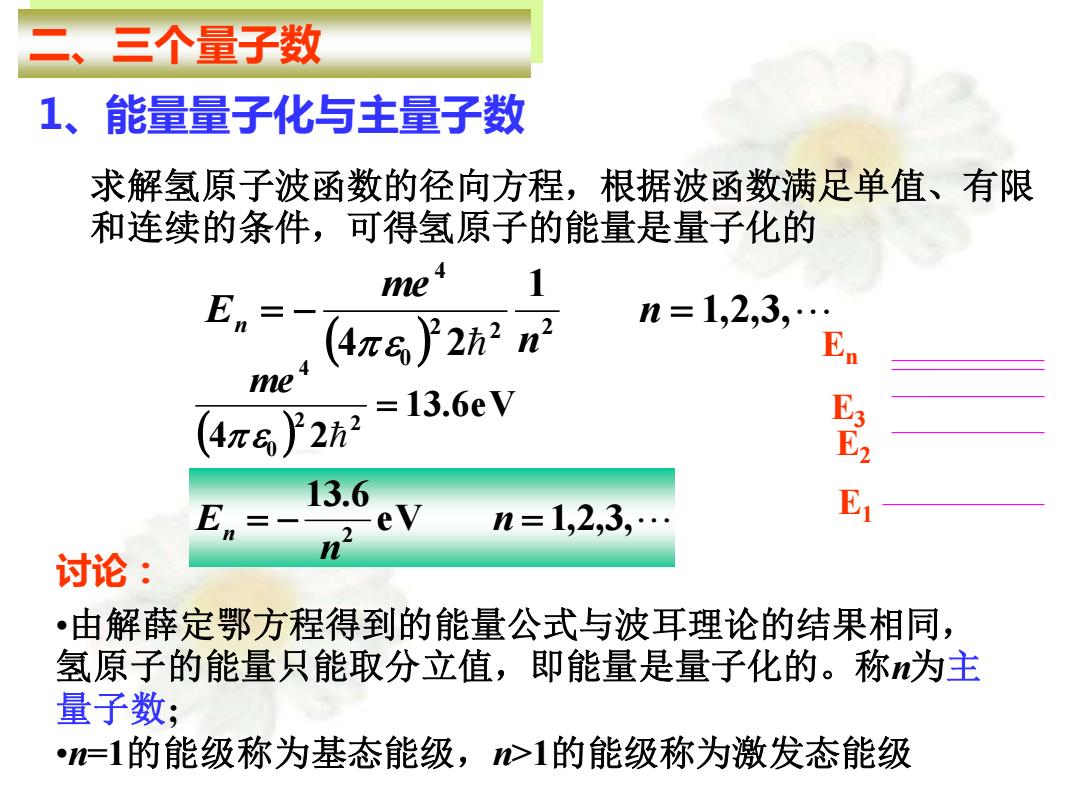
二、三个量子数 1、能量量子化与主量子数 求解氢原子波函数的径向方程,根据波函数满足单值、有限 和连续的条件,可得氢原子的能量是量子化的 ( ) 1,2,3, 1 4 2 2 2 2 0 4 = − n = n me En ( ) 13.6eV 4 2 2 2 0 4 = me eV 1,2,3, 13.6 2 = − n = n En E1 E2 E3 En 讨论: •由解薛定鄂方程得到的能量公式与波耳理论的结果相同, 氢原子的能量只能取分立值,即能量是量子化的。称n为主 量子数; •n=1的能级称为基态能级,n>1的能级称为激发态能级

2、角动量量子化与角量子数 求解氢原子波函数的经度方程,可得氢原子中电子的角动量 是量子化的 =0+22=70+ l=0,1,2,…,n-1 其中1叫做轨道角动量量子数或角量子数。 讨论: 波耳理论的L=nh/2元,最小值为h/2元;而量子力学得出角 动量的最小值为0。实验证明,量子力学得结论是正确的: •角量子数要受到主量子数得限制:处于能级E的原子,其 角动量共有n种可能的取值,即0,1,2,.,n-1; •通常用主量子数和代表角量子数的字母一起来表示原子的 状态。 1s表示原子的基态:=1,=0, =0s1=1 P 2p表示原子处于第一激发态:=2,=1, =2d=3 f
2、角动量量子化与角量子数 求解氢原子波函数的经度方程,可得氢原子中电子的角动量 是量子化的 ( ) ( 1) 0,1,2, , 1 2 = +1 = l l + l = n− h L l l 其中l 叫做轨道角动量量子数或角量子数。 讨论: •波耳理论的L=nh/2,最小值为h/2;而量子力学得出角 动量的最小值为0。实验证明,量子力学得结论是正确的; •角量子数要受到主量子数得限制:处于能级En的原子,其 角动量共有n种可能的取值,即l=0,1,2,…,n-1; •通常用主量子数和代表角量子数的字母一起来表示原子的 状态。 1s表示原子的基态:n=1,l=0, 2p表示原子处于第一激发态:n=2,l=1, l=0 s l=1 p l=2 d l=3 f
氢原子内电子的状态 1=01=11=21=3 1=41=5 S p d f 8 h n=1 1s n=2 25 2p n=3 3s 3p 3d n=4 4s Ap 4d Af n=5 5s Sp 5d 5f 5g n=6 6s 6p 6d 6f 6g 6h
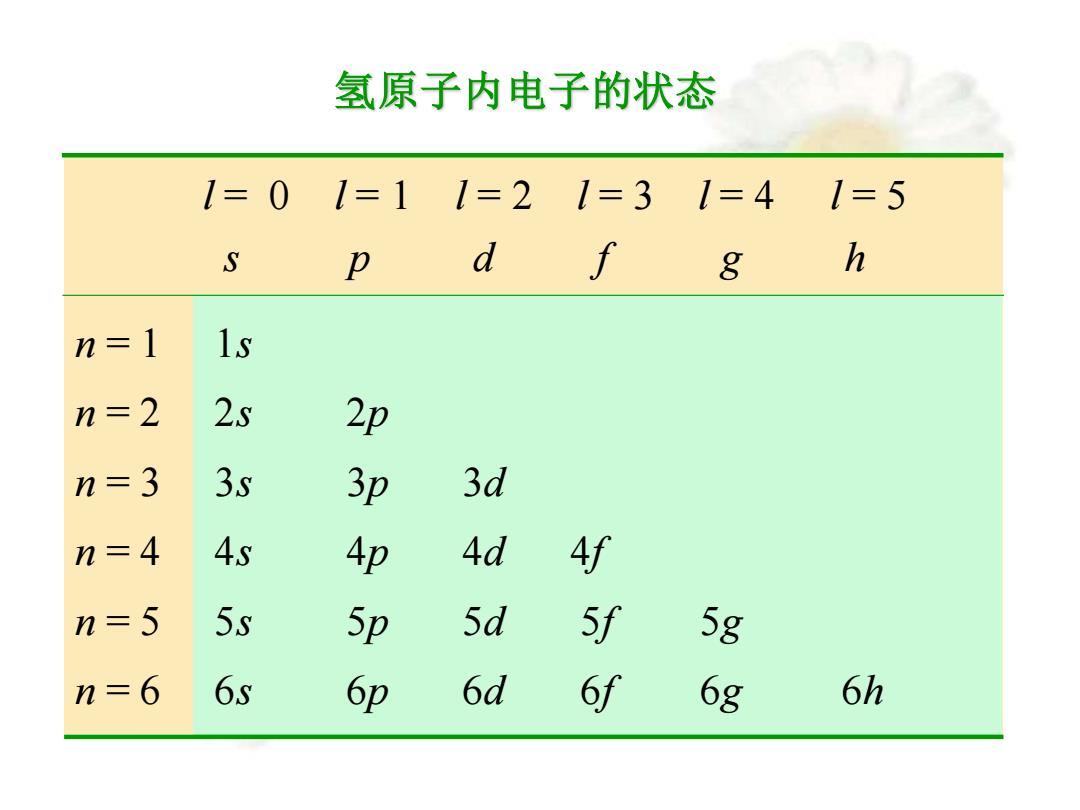
氢原子内电子的状态 l = 0 l = 1 l = 2 l = 3 l = 4 l = 5 s p d f g h n = 1 1s n = 2 2s 2p n = 3 3s 3p 3d n = 4 4s 4p 4d 4f n = 5 5s 5p 5d 5f 5g n = 6 6s 6p 6d 6f 6g 6h

3、空间量子化与磁量子数 求解氢原子波函数的纬度方程,可得氢原子中电子的角动量 在某特定方向的分量是量子化的 h L.=m42元 m=0,±1,±2,…±l ,叫做轨道角动量磁量子数,简称磁量子数。角动量的 这种取向特性叫做空间量子化。 说明:对于一定大小的角动 量,m=0,士1,士2,…士l, mF2 共有2+1种可能的取值。对 每一个m,角动量L与Z轴 m1 的夹角日应满足 m0 m-1 L. m mF-2
3、空间量子化与磁量子数 求解氢原子波函数的纬度方程,可得氢原子中电子的角动量 在某特定方向的分量是量子化的 m l h Lz = ml l = 0,1,2, 2 ml叫做轨道角动量磁量子数,简称磁量子数。角动量的 这种取向特性叫做空间量子化。 说明:对于一定大小的角动 量,ml =0,±1,±2,…±l, 共有2l+1种可能的取值。对 每一个ml ,角动量L与Z轴 的夹角 应满足 ( 1) cos + = = l l m L Lz l ml= 0 ml= 1 ml= 2 ml=−2 ml= − 1

塞曼效应 1896年,塞曼发现在磁场中谱线分裂的现象。塞曼和洛伦 兹用用经典理论作了分析。为此,他们于1902年共同获得 了诺贝尔物理学奖金。但是只有量子力学才能对塞曼效应 作出全面解释。 塞曼效应可以用空间量 子化来说明。 如图所示,在外磁场中,对 于=1的能级,共有三个量子 态,即m0,±1,于是从能 级=1的三个量子态分别跃迁 =1 到能级=0时,就产生了三条 m斤-1 谱线,这种现象,称为正常 塞曼效应。 =0 反常塞曼效应:有些元素,例如钠谱线在弱磁场中分裂为四 条、六条谱线,这种现象称为反常塞曼效应。1926年,海森 伯考虑了电子的自旋后,才用量子力学对反常塞曼效应给出 了正确的说明
塞曼效应 1896年,塞曼发现在磁场中谱线分裂的现象。塞曼和洛伦 兹用用经典理论作了分析。为此,他们于1902年共同获得 了诺贝尔物理学奖金。但是只有量子力学才能对塞曼效应 作出全面解释。 l=1 l=0 ml=0 ml= -1 ml=1 塞曼效应可以用空间量 子化来说明。 如图所示,在外磁场中,对 于l=1的能级,共有三个量子 态,即ml=0, ±1,于是从能 级l=1的三个量子态分别跃迁 到能级l=0时,就产生了三条 谱线,这种现象,称为正常 塞曼效应。 反常塞曼效应:有些元素,例如钠谱线在弱磁场中分裂为四 条、六条谱线,这种现象称为反常塞曼效应。1926年,海森 伯考虑了电子的自旋后,才用量子力学对反常塞曼效应给出 了正确的说明