
海大理学院教学裸件 大学物理学电子教案 简谐运动的基本概念 机械振动引言 14一1简谐运动 14一2简谐运动的振幅、周期、频 率和相位 14一3旋转矢量
大学物理学电子教案 海大理学院教学课件 简谐运动的基本概念 机械振动引言 14-1 简谐运动 14-2 简谐运动的振幅、周期、频 率和相位 14-3 旋转矢量
第十四章 机械振动 一、什么是振动 从狭义上说,通常把具有时间 周期性的运动称为振动。 从广义上说,任何一个物理量 在某一数值附近作周期性的变化, 都称为振动
第十四章 机械振动 一、什么是振动 从狭义上说,通常把具有时间 周期性的运动称为振动。 从广义上说,任何一个物理量 在某一数值附近作周期性的变化, 都称为振动

什么是机械振动 机械振动是物体在一定位置附近所作的周期性往 复的运动。 三、研究机械振动的意义 •不同类型的振动虽然有本质的区别,但振动量随时间 的变化关系遵循相同的数学规律,从而不同的振动有 相同的描述方法。 •研究机械振动的规律是学习和研究其它形式的振动以 及波动、无线电技术、波动光学的基础
二、什么是机械振动 机械振动是物体在一定位置附近所作的周期性往 复的运动。 三、研究机械振动的意义 •不同类型的振动虽然有本质的区别,但振动量随时间 的变化关系遵循相同的数学规律,从而不同的振动有 相同的描述方法。 •研究机械振动的规律是学习和研究其它形式的振动以 及波动、无线电技术、波动光学的基础
14-1 简谐运动 研究简谐运动的意义 •在一切振动中,最简单和最基本的振动称为简谐运动 •任何复杂的运动都可以看成是若干简谐运动的合成 简谐运动 1、弹簧振子 2、弹簧振子运 B 动的定性分析 BO:弹性力向右, 加速度向右,加速; 0→C: 向左, 向左,减速; C→0: 向左, 向左,加速; O→B: 向右, 向右,减速。 物体在B、C之间来回往复运动 3、 畅体作简谐运动的条件 物体的惯性 阻止系统停留在平衡位置 作用在物体上的弹性力一 驱使系统回复到平衡位置
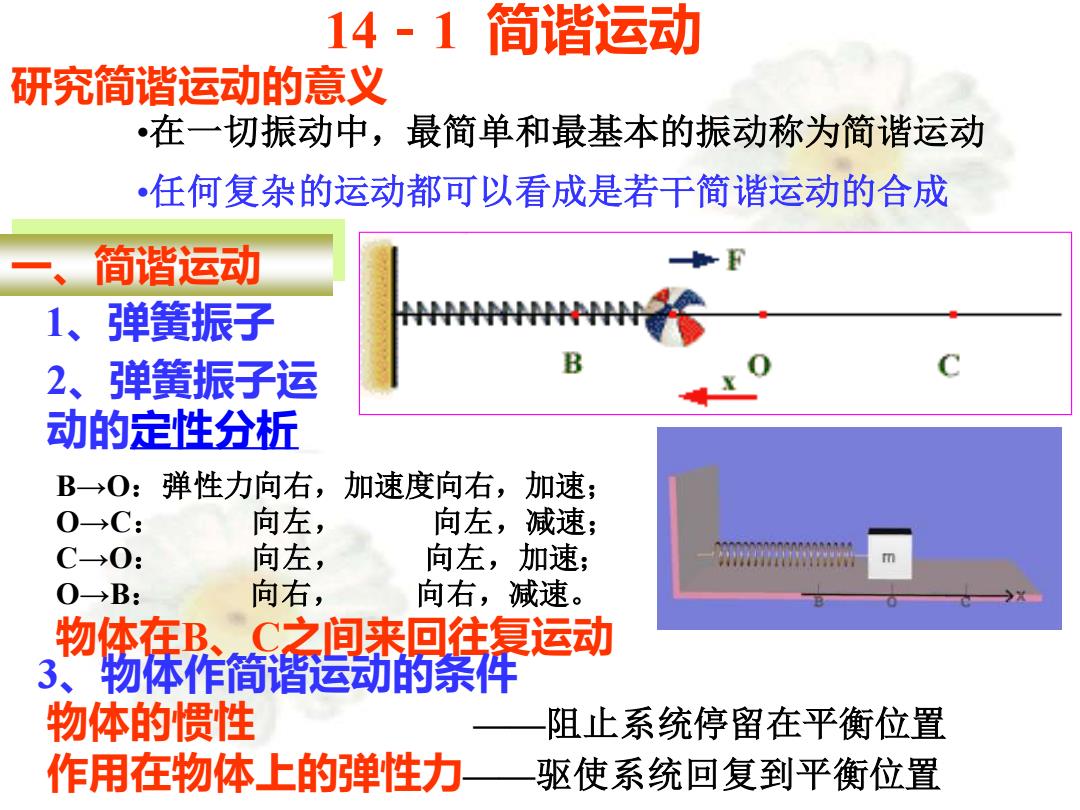
14-1 简谐运动 研究简谐运动的意义 •在一切振动中,最简单和最基本的振动称为简谐运动 •任何复杂的运动都可以看成是若干简谐运动的合成 一、简谐运动 1、弹簧振子 2、弹簧振子运 动的定性分析 B→O:弹性力向右,加速度向右,加速; O→C: 向左, 向左,减速; C→O: 向左, 向左,加速; O→B: 向右, 向右,减速。 物体在B、C之间来回往复运动 3、物体作简谐运动的条件 物体的惯性 ——阻止系统停留在平衡位置 作用在物体上的弹性力——驱使系统回复到平衡位置
4、弹簧振子的动力学特征 取平衡位置O 点为坐标原点, 水平向右为x 轴的正方向。 f=一x 力的方向与位移的方向相反,始终指向平衡位置的,称为 回复力。 简谐运动 f ma m 微分方程 n 02 m dx+o'x-0
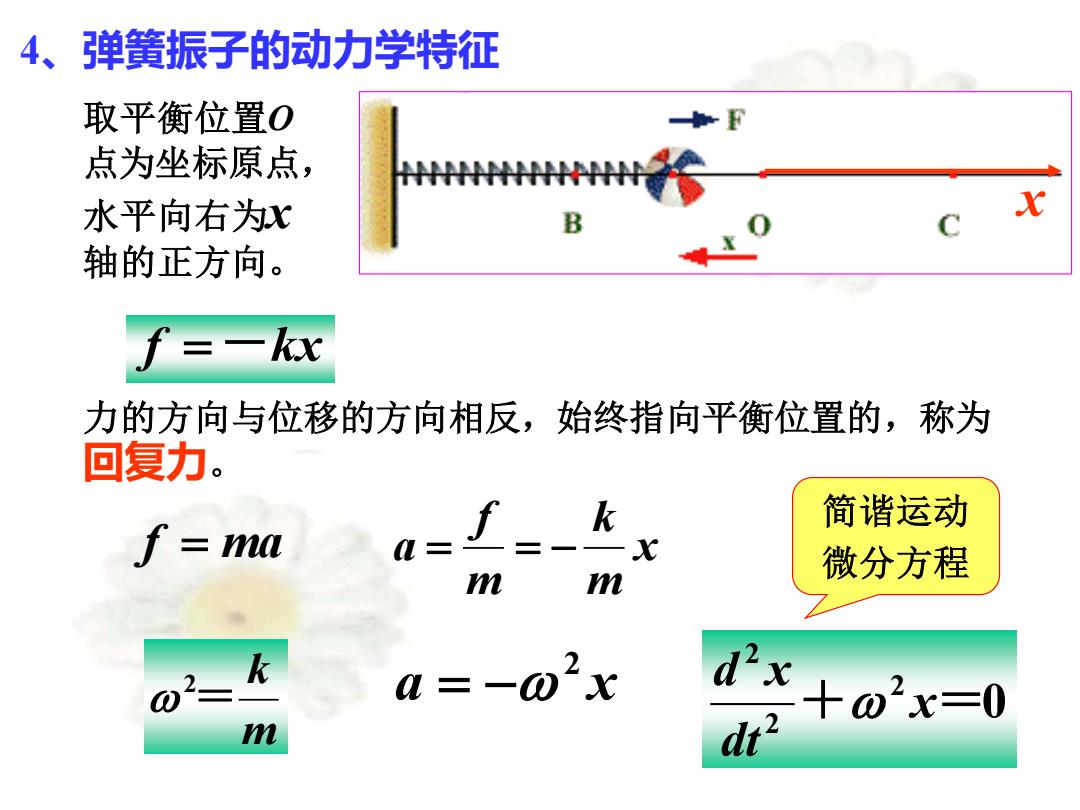
4、弹簧振子的动力学特征 取平衡位置O 点为坐标原点, 水平向右为x 轴的正方向。 x f =-kx 力的方向与位移的方向相反,始终指向平衡位置的,称为 回复力。 f = ma x m k m f a = = − m k 2 = 0 2 2 2 + x= dt d x a x 2 = − 简谐运动 微分方程
5、简谐运动的运动学特征 x=Acos(@t+o) xt七,以,a V= =-Asin(@t+o) dt d'x dr2 -=-@2Acos(@t+p) 说明: 物体在简谐运动时,其位移、速度、加速度都是周期性变 化的 ·简谐运动不仅是周期性的,而且是有界的,只有正弦函数、 余弦函数或它们的组合才具有这种性质,这里我们采用余弦 函数
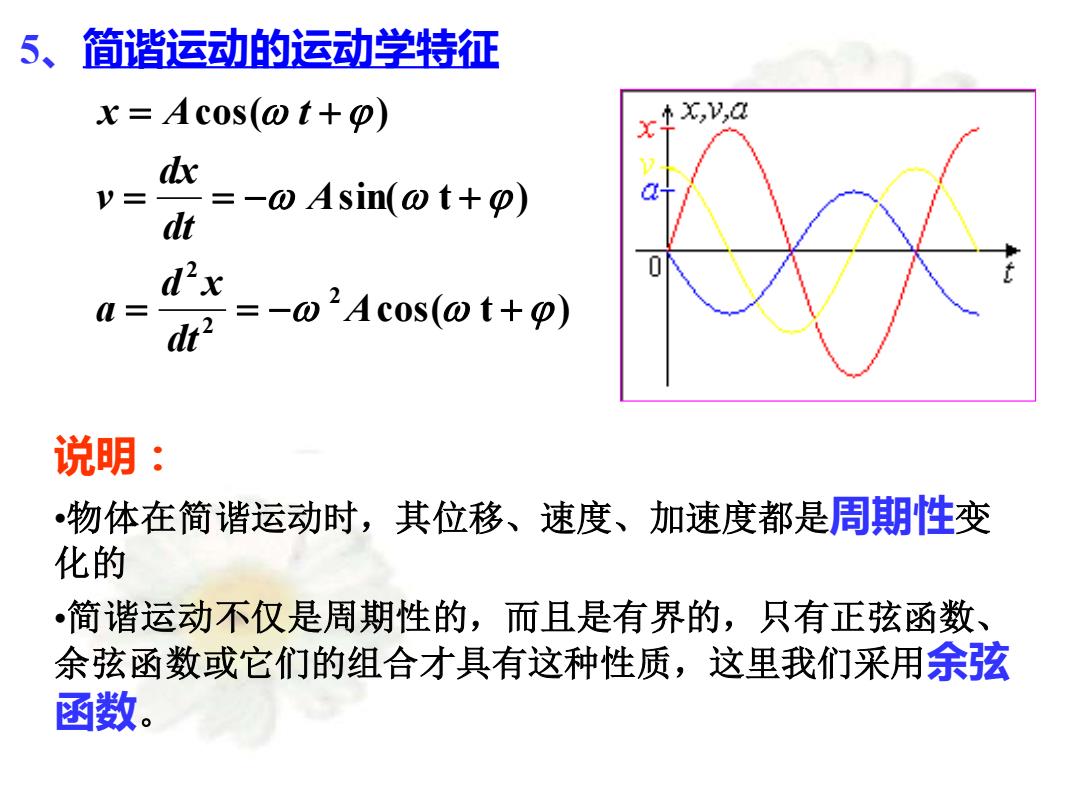
5、简谐运动的运动学特征 cos( t ) sin( t ) cos( ) 2 2 2 = = − + = = − + = + A dt d x a A dt dx v x A t 说明: •物体在简谐运动时,其位移、速度、加速度都是周期性变 化的 •简谐运动不仅是周期性的,而且是有界的,只有正弦函数、 余弦函数或它们的组合才具有这种性质,这里我们采用余弦 函数

简谐运动的特点 1、从受力角度来看一动力学特征 f=一kx 2、从加速度角度来看 —运动学特征 2 M=-0X 3、从位移角度来看一运动学特征 x=Acos(@t+o) 说明: 要证明一个物体是否作简谐运动,只要证明上面三个式子中的 一个即可,且由其中的一个可以推出另外两个; 要证明一个物体是否作简谐运动最简单的方法就是受力方析, 得到物体所受的合外力满足回复力的关系
二、简谐运动的特点 1、从受力角度来看——动力学特征 f =-kx 2、从加速度角度来看——运动学特征 a x 2 = − 3、从位移角度来看——运动学特征 x = Acos( t +) 说明: •要证明一个物体是否作简谐运动,只要证明上面三个式子中的 一个即可,且由其中的一个可以推出另外两个; •要证明一个物体是否作简谐运动最简单的方法就是受力方析, 得到物体所受的合外力满足回复力的关系
例1、一个轻质弹簧竖直悬挂,下端挂一质量为的物体。今将 物体向下拉一段距离后再放开,证明物体将作简谐振动。 解: 求平衡位置 弹簧原长 kx。=mg 20 mg 尤。= 挂m后伸长 受弹力 k 以平衡位置0为原点 平衡位置 X。 F=mg-k(xo+x) mg -kxco -kx 伸长 =-x 某时刻m位置 因此,此振动为简谐振动
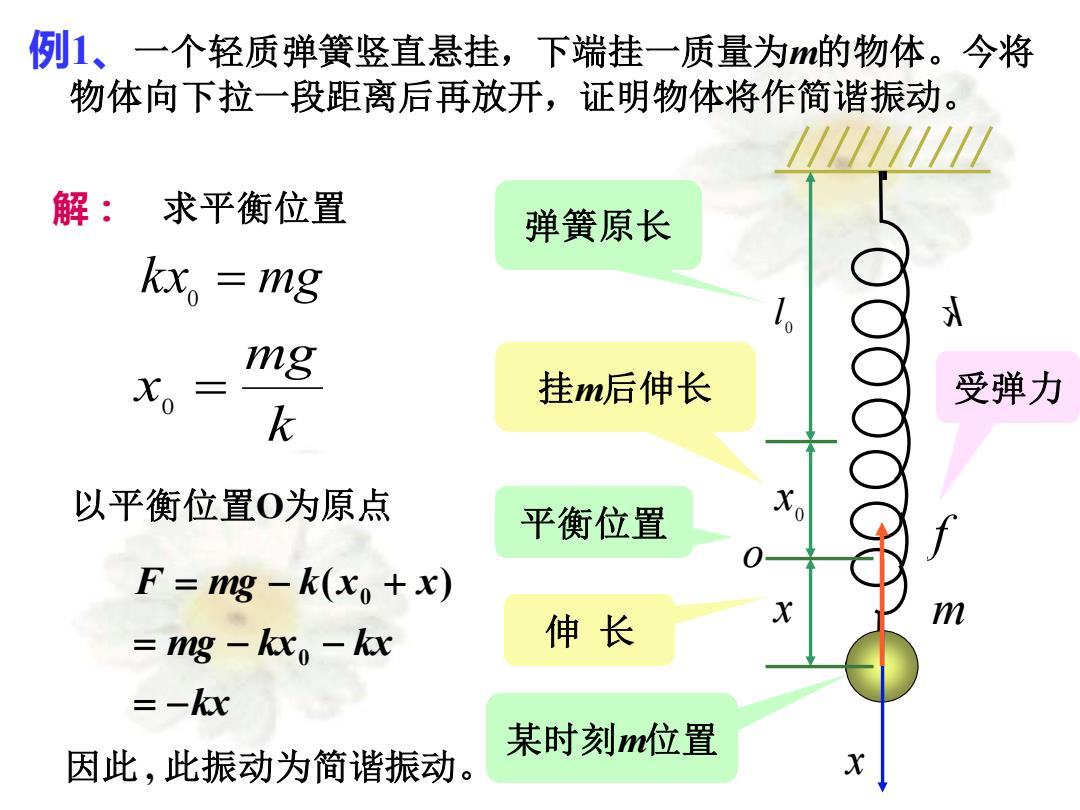
例1、一个轻质弹簧竖直悬挂,下端挂一质量为m的物体。今将 物体向下拉一段距离后再放开,证明物体将作简谐振动。 因此 , 此振动为简谐振动。 m 0 l k 0 x x x o 以平衡位置O为原点 弹簧原长 挂m后伸长 某时刻m位置 f 伸 长 受弹力 平衡位置 解: 求平衡位置 kx = mg 0 k mg x0 = kx mg kx kx F mg k x x = − = − − = − + 0 0 ( )
14-2简谐运动的振幅、周期、 频率和相位 振幅一反映振动幅度的大小 1、定义—A 作简谐运动的物体 H谷谷谷 离开平衡位置的最 0 B、C为弹簧振子两极端位置,则A-0B=0C 大位移的绝对值。 2、说明 振幅恒为正值,单位为米(m); 振幅的大小与振动系统的能量有关,由系统的初 始条件确定
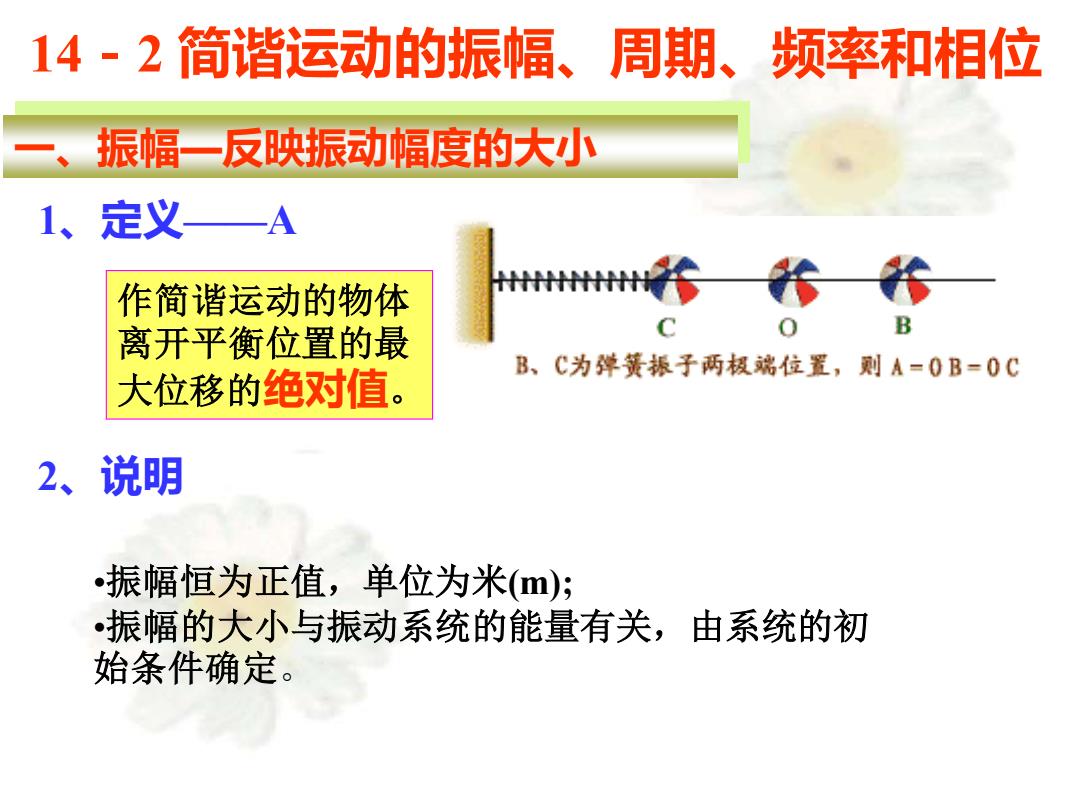
14-2 简谐运动的振幅、周期、频率和相位 一、振幅—反映振动幅度的大小 1、定义——A 作简谐运动的物体 离开平衡位置的最 大位移的绝对值。 2、说明 •振幅恒为正值,单位为米(m); •振幅的大小与振动系统的能量有关,由系统的初 始条件确定

二、周期与频率一反映振动的快慢 1、周期 定义:物体作一次完全振动所需的时间,用T表示,单位 为秒(s) x=Acos(@t+o)=Acos @(t+T)+o] oT=2元 2元 2、频率 定义:单位时间内物体所作的完全振动的次数,用ⅴ表 示,单位为赫兹Hz
二、周期与频率—反映振动的快慢 1、周期 定义:物体作一次完全振动所需的时间,用T表示,单位 为秒(s) x = Acos( t +) = Acos[( t +T) +] T=2 2 T = 2、频率 定义:单位时间内物体所作的完全振动的次数,用ν表 示,单位为赫兹(Hz)。 2 1 = T =