
海大理学院教学保件 大学物理学电子教案 光的干涉(2) 17-3光程薄膜干涉 17-4劈尖牛顿环 17-5迈克耳孙干涉仪
大学物理学电子教案 海大理学院教学课件 光的干涉(2) 17-3 光程 薄膜干涉 17-4 劈尖 牛顿环 17-5 迈克耳孙干涉仪

复习 光的干涉理论 杨氏干涉 ·实验装置 。 干涉条件 ·条纹特点 ·菲涅耳双面镜、洛埃镜、菲涅耳双棱镜
复 习 • 光的干涉理论 • 杨氏干涉 • 实验装置 • 干涉条件 • 条纹特点 • 菲涅耳双面镜、洛埃镜、菲涅耳双棱镜

§17-3光程薄膜干涉 B 光程 光在介质中的传播 1、光程的引入和光程的概念 AAAA u c Ao 九=uT=“= 例1、 n==√8,l, ny n S1 ·在介质中传播的波长,折算 成真空中波长 n 光程=nr=二r=cAt S2 •光在介质中传播的距离折算 D = 成真空中的长度。 D2 na+r2-a 2、光程差 两光程之差叫做光程差 6=D2-D1 δ=n22-n =3-h+(n-1)a 相位差: p=2(5-)=2 (n22-n)= 26 20
一、光程 光在介质中的传播 •光在介质中传播的距离折算 成真空中的长度。 r c t u c 光程= nr = = n n u c uT 0 = = = = r r u c n = = A B n r •在介质中传播的波长,折算 成真空中波长 两光程之差叫做光程差 2 2 1 1 = n r − n r 2 ( ) 1 1 2 2 r r 相位差: = − 0 2 2 1 1 0 2 ( ) 2 = n r − n r = 2、光程差 1、光程的引入和光程的概念 §17-3 光程 薄膜干涉 例1、 n 1 S 2 S 1 r 2 r P a D2 = na +r 2 −a 1 1 D = r = D2 − D1 = r2 − r1 +(n−1)a
二 透镜不引起附加的光程差 SC=SA SB=SF CD+n·DE+EF=n·ABS A 演示1 •当用透镜观测 ·演示2 干涉时,不会 结论: 带来附加的光 程差。 干涉条件 用相位差表示: ±2k元 k=0,1,2,. 明条纹 △0= ±k-0好 k=1,2,3,… 暗条纹 •用光程差表示: ±k兄 k=0,1,2,..明条纹,半波长的偶数倍 8= k=0,1,2,.…暗条纹,半波长的奇数培
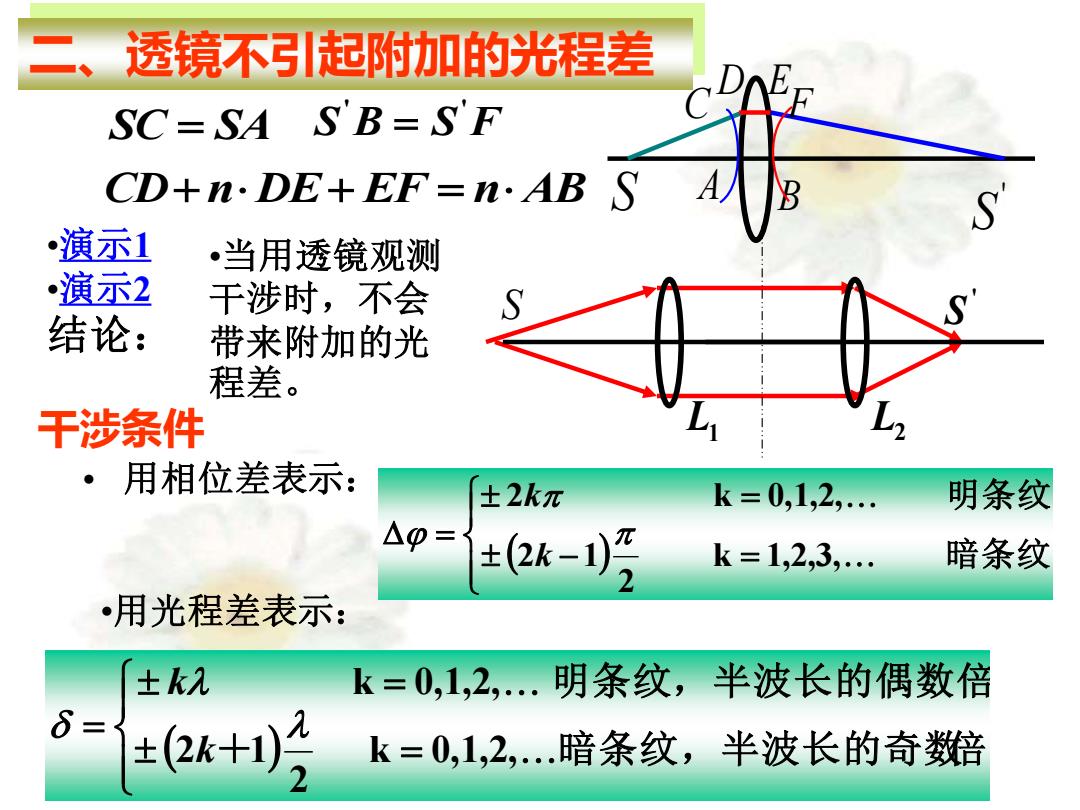
•当用透镜观测 干涉时,不会 带来附加的光 程差。 SC = SA S B S F ' ' = CD+ n DE+ EF = n AB S C D E F A B ' S 二、透镜不引起附加的光程差 S ' S L1 L2 •演示1 •演示2 结论: 干涉条件 • 用相位差表示: ( ) − = = = 暗条纹 明条纹 k 1,2,3, 2 2 1 2 k 0,1,2, k k •用光程差表示: ( ) = = = + 暗条纹,半波长的奇数倍 明条纹,半波长的偶数倍 k 0,1,2, 2 2 1 k 0,1,2, k k
三、薄膜干涉 1、i 引言: 薄膜干涉属于分振幅法 2、 实验装置 B.Interference produced by reflecting white light from a soap film.The picture on the right shows the patter produced by red light. 在一均匀透明介质n1中放入 上下表面平行,厚度为e的 均匀介质n2, 光与光的光程差为: δ=(AC+BC)n2-ADn,+九/2 n 有半波损失
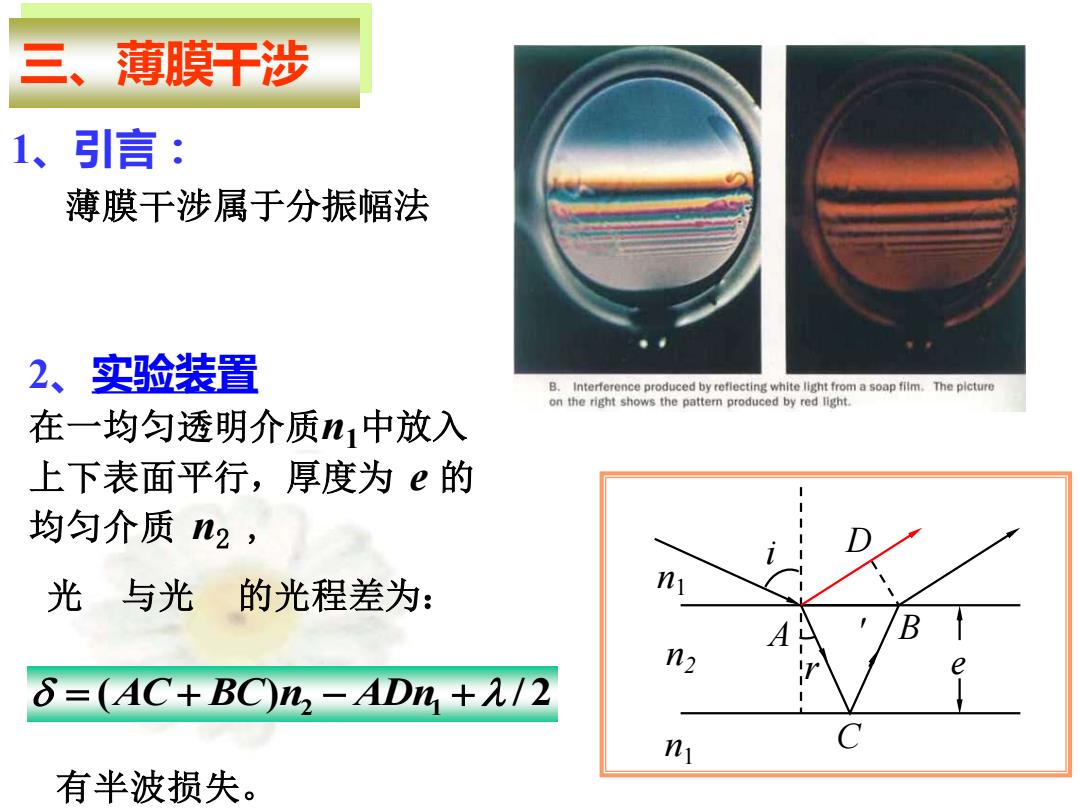
三、薄膜干涉 1、引言: 薄膜干涉属于分振幅法 2、实验装置 在一均匀透明介质n1中放入 上下表面平行,厚度为 e 的 均匀介质 n2 , 光 与光 的光程差为: = (AC + BC)n2 − ADn1 + / 2 有半波损失。 n1 n2 n1 A B C e D r i

3、光程差 由折射定律和几何关系可得出: n sini=n siny AD=ABsini AB=2etgy AC=BC=e/cosy 代入6=(AC+BC)n2-ADn+九/2 得出:6=2n2( 1 simY+元12 结论:相同的入射角对 osY 应同一级条纹。因此,称它 为薄膜等倾干涉。 即:δ=2en,cosy+λ/2 光与光 相遇在无穷远, 或者在透镜的焦平面上观察 或写为:6=2eVm-所·sim2i+元/2 它们的相干结果,所以称它 为定域干涉。 k入 k=1,2,3,…,明纹 =2店-msimi+2k+月 k=0,1,2,…暗纹
3、光程差 由折射定律和几何关系可得出: AB = 2etg AC = BC = e / cos sin sin 1 n2 n i = AD = ABsini 代入 = (AC + BC)n2 − ADn1 + / 2 ) / 2 cos sin cos 1 2 ( 2 2 得出: = en − + 即: = 2en2 cos + / 2 或写为: 2 sin / 2 2 2 1 2 = e n2 − n i + 结论:相同的入射角对 应同一级条纹。因此,称它 为薄膜等倾干涉。 光 与光 相遇在无穷远, 或者在透镜的焦平面上观察 它们的相干结果,所以称它 为定域干涉。 ( ) + = = = − + 暗 纹 明 纹 = 0,1,2, 2 2 1 1 2 3 2 2 sin 2 2 1 2 2 k k k k , , , , e n n i n1 n2 n1 A B C e D r i

4、 透射光的干涉: 对于同一厚度的薄膜,在某一 方向观察到某一波长对应反射 光相干相长,则该波长在对应 方向的透射光一定相干相消。 因为要满足能量守恒。 增透膜、增反膜用在光学仪器的镜头 上,就是根据这个道理。 空气1.00 MgF272=1.3器 玻璃g-1.50 5、应用: •测定薄膜的厚度; 测定光的波长; •提高或降低光学器件的透射率一增透膜(增反膜)
4、透射光的干涉: 对于同一厚度的薄膜,在某一 方向观察到某一波长对应反射 光相干相长,则该波长在对应 方向的透射光一定相干相消。 因为要满足能量守恒。 增透膜、增反膜用在光学仪器的镜头 上,就是根据这个道理。 A B C D 1 n 1 n 2 n e i 5、应用: •测定薄膜的厚度; •测定光的波长; •提高或降低光学器件的透射率——增透膜(增反膜)

例题.如图所示,在折射率为1.50的平 白光 反射相干光 板玻璃表面有一层厚度为300nm,折射 空气 =1.00 率为1.22的均匀透明油膜,用白光垂直 油膜 2=1.22 e %=1.50 射向油膜,问: 玻璃分 透射相干光 1)哪些波长的可见光在反射光中产生 相长干涉? k=1时 红光 2)哪些波长的可见光在透射光中产生 相长干涉? 2=2×1.22×300=732nm 3)若要使反射光中=550nm的光产生 相干涉,油膜的最小厚度为多少? =2时 紫外 解:()因反射光之间没有半波损失, 由垂直入射=0,得反射光相长干涉的 2=2×1.22×300/2=366nm 条件为 δ=2n2e=k2, k=1,2,3… 故反射中红光产 生相长干涉。 = 2nze k
例题.如图所示,在折射率为1.50的平 板玻璃表面有一层厚度为300nm,折射 率为1.22的均匀透明油膜,用白光垂直 射向油膜,问: 1)哪些波长的可见光在反射光中产生 相长干涉? 2)哪些波长的可见光在透射光中产生 相长干涉? 3)若要使反射光中λ=550nm的光产生 相干涉,油膜的最小厚度为多少? 解:(1)因反射光之间没有半波损失, 由垂直入射i=0,得反射光相长干涉的 条件为 = 2n2 e = k, k = 1,2,3 k n e2 2 = k=1时 1 = 21.22300 = 732nm 红光 k=2时 2 = 21.22 300/ 2 = 366nm 故反射中红光产 生相长干涉。 紫外

2)对于透射光,相干条件为: (3)由反射相消干涉条件为: 6=2n2e+=k2, k=1,2,3… 6=2e=2k+1,k=0,12, Ane 2k-1 e=2k+1以 =1时 红外 42 元=4n2e=4×1.22×300=1464nm 显然=O所产生对应的厚 =2时 青色光 度最小,即 2=4n2e/3=4×1.22×300/3=488nm 2550 =3时 紫外 emin= 42 =113nm 4×1.22 3=4m2e/5=4×1.22×300/5=293nm
(2)对于透射光,相干条件为: , 1,2,3 2 = 2n2 e = k k = + 2 1 4 2 k- n e = k=1时 1 = 4n2 e=41.22 300 = 1464nm 红外 k=2时 2 = 4n2 e / 3=41.22 300/ 3 = 488nm 青色光 k=3时 3 = 4n2 e / 5=41.22 300/ 5 = 293nm 紫外 (3)由反射相消干涉条件为: ( ) , 0,1,2, 2 = 2n2 e = 2k 1 k = + ( ) 4 2 2 1 n k e + = 显然k=0所产生对应的厚 度最小,即 nm n e 113 4 1.22 550 4 2 min = = =
§17-4劈尖牛顿环 劈尖干涉 1、 劈尖王涉的实验装置 干涉条纹定域 在膜附近。条 纹形状由膜的 2e+2/2=k2 等厚点轨迹所 明纹中心 决定。 2e+/2=(2k+1)2/2 暗纹中心 2、干涉条件 k=0,士1,±2…
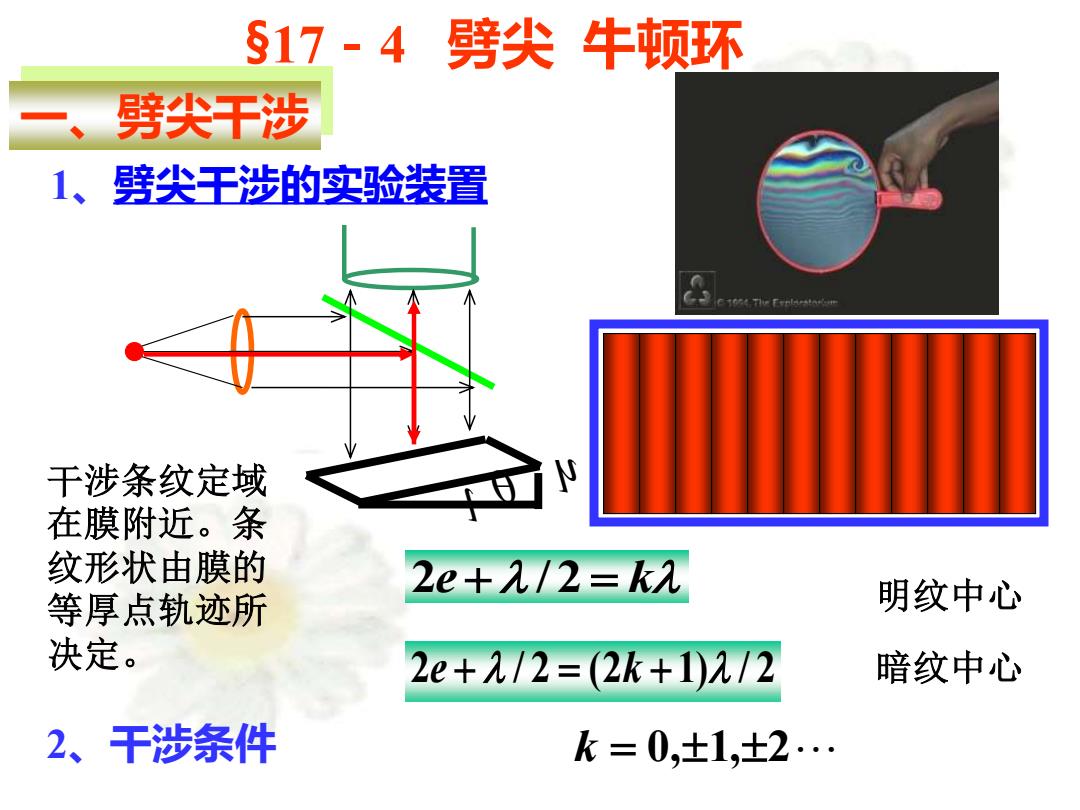
干涉条纹定域 在膜附近。条 纹形状由膜的 等厚点轨迹所 决定。 一、劈尖干涉 h l 1、劈尖干涉的实验装置 §17-4 劈尖 牛顿环 2e + / 2 = k 2e + / 2 = (2k + 1) / 2 k = 0,1,2 明纹中心 暗纹中心 2、干涉条件