广东海洋大学：《大学物理》课程教学资源（PPT课件）lesson32 电磁学习题讨论课（导体和绝缘体）

电磁学习题讨论课2 导体和绝缘体 1.无限大均匀带电平面板附近场强为σ/20，对 靠近有限大带电表面的地方也适用。但导体表面 附近场强为σ/？ 6/2e 6/280 S

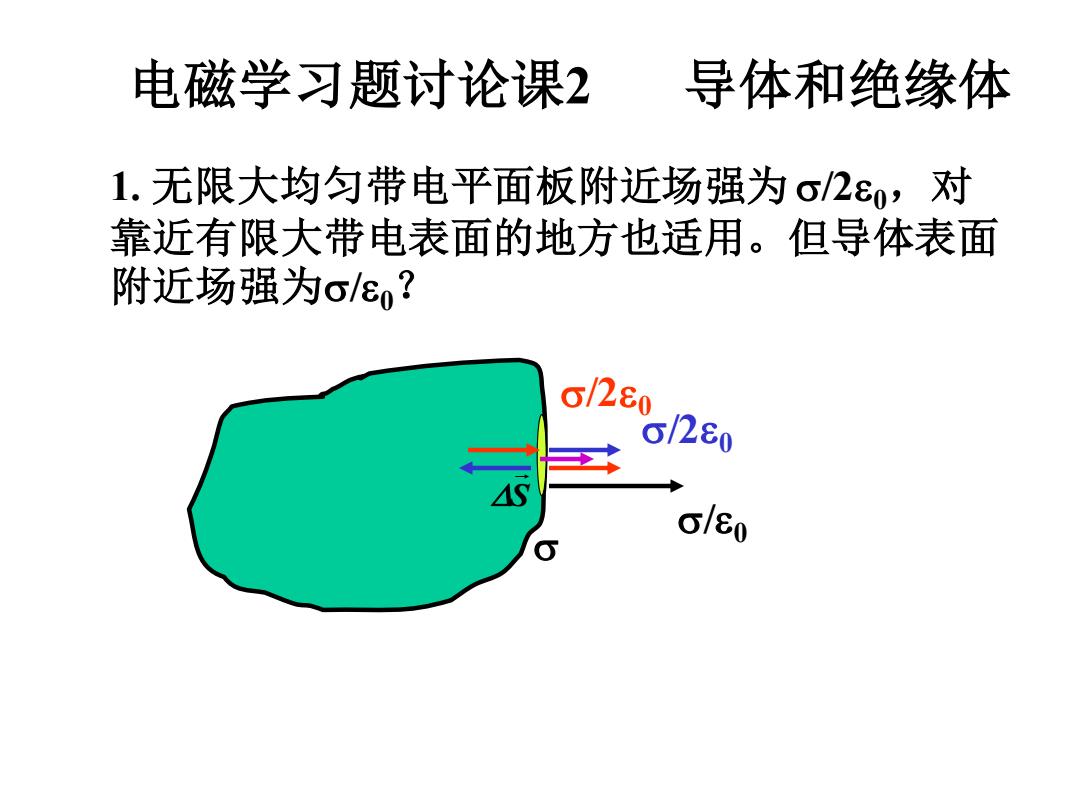
电磁学习题讨论课2 导体和绝缘体 1. 无限大均匀带电平面板附近场强为 /20，对 靠近有限大带电表面的地方也适用。但导体表面 附近场强为/0？  S   /20 /0 /20

2.在一个绝缘的不带电的导体球周围做一同心球面的 高斯面，定性讨论将一正电荷q移向高斯面上A点的过 程， (1)A点处的场强大小和方向怎样变化？ (2)B点处的场强大小和方向怎样变化？ (3)过S面的电通量怎样变化？ q B 电通量不变

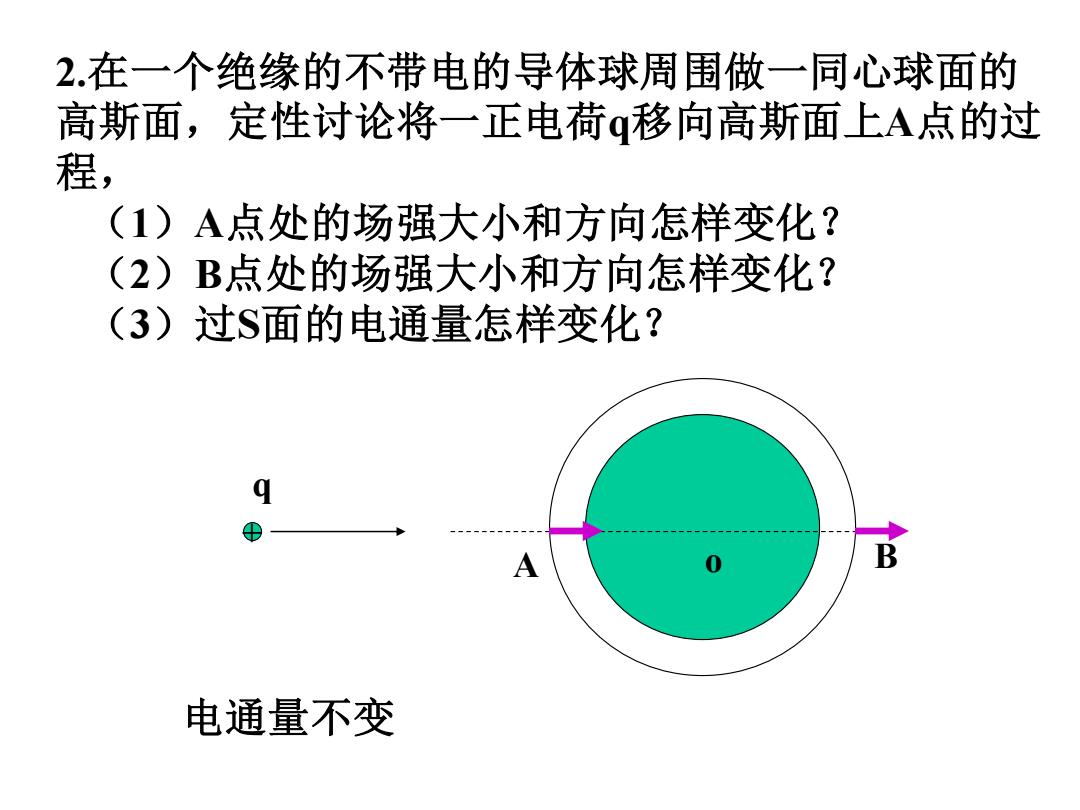
2.在一个绝缘的不带电的导体球周围做一同心球面的 高斯面，定性讨论将一正电荷q移向高斯面上A点的过 程， （1）A点处的场强大小和方向怎样变化？ （2）B点处的场强大小和方向怎样变化？ （3）过S面的电通量怎样变化？ A o B q 电通量不变 +

3.一不接地的球形金属壳不带电，现球心处放一 正电荷q1,在球壳外放一点电荷q2,问： (1)q2能否感受q1的场的作用； (2)q1能否感受电场力的作用： (3)q1在球壳内运动，q2能否感受得到？ 若q1数值变化时又如何？ (4) 若将球壳接地以上三问的答案又如何？ 92 (4) (1)不能 (1)能 91 (2)不能 (2)不能 (3)都不能 (3)不能，能

3.一不接地的球形金属壳不带电，现球心处放一 正电荷q1，在球壳外放一点电荷q2，问： （1） q2能否感受q1的场的作用； （2） q1能否感受电场力的作用； （3） q1在球壳内运动，q2能否感受得到？ 若q1数值变化时又如何？ （4） 若将球壳接地以上三问的答案又如何？ q1 q2 （1）能 （2）不能 （3）不能，能 （1）不能 （2）不能 （3）都不能 (4)

4.半径为r1、r2(r2>1)的互相绝缘的二同心导体 球壳，内球壳带电+q,外球壳带电Q,问： (1)外球壳的电荷和电势； (2)外球壳接地后重新绝缘，外球壳的电荷和电势； (3)然后内球壳接地，内球壳的电势和外球壳的电 势和（2)相比各改变了多少？ 2+q 解 :(1)无限远处电势为零 00 U,=∫E而= 9+Q 4元82 电荷2+q 壳厚度远小于半径

4.半径为r1、r2（ r2 >r1）的互相绝缘的二同心导体 球壳，内球壳带电+q，外球壳带电Q，问： （1）外球壳的电荷和电势； （2）外球壳接地后重新绝缘，外球壳的电荷和电势； （3）然后内球壳接地，内球壳的电势和外球壳的电 势和（2）相比各改变了多少？ （1）无限远处电势为零   + =  = 2 r 0 2 2 4 r q Q U E dr     电荷Q+q r1 r2 q Q 解： -q +q 壳厚度远小于半径

(2)外球壳接地，球壳外电场为零，q+Q电荷流 入大地，外球壳带电-，电势为零。 0 (2) (3) (3)内球壳接地，剩余电荷9

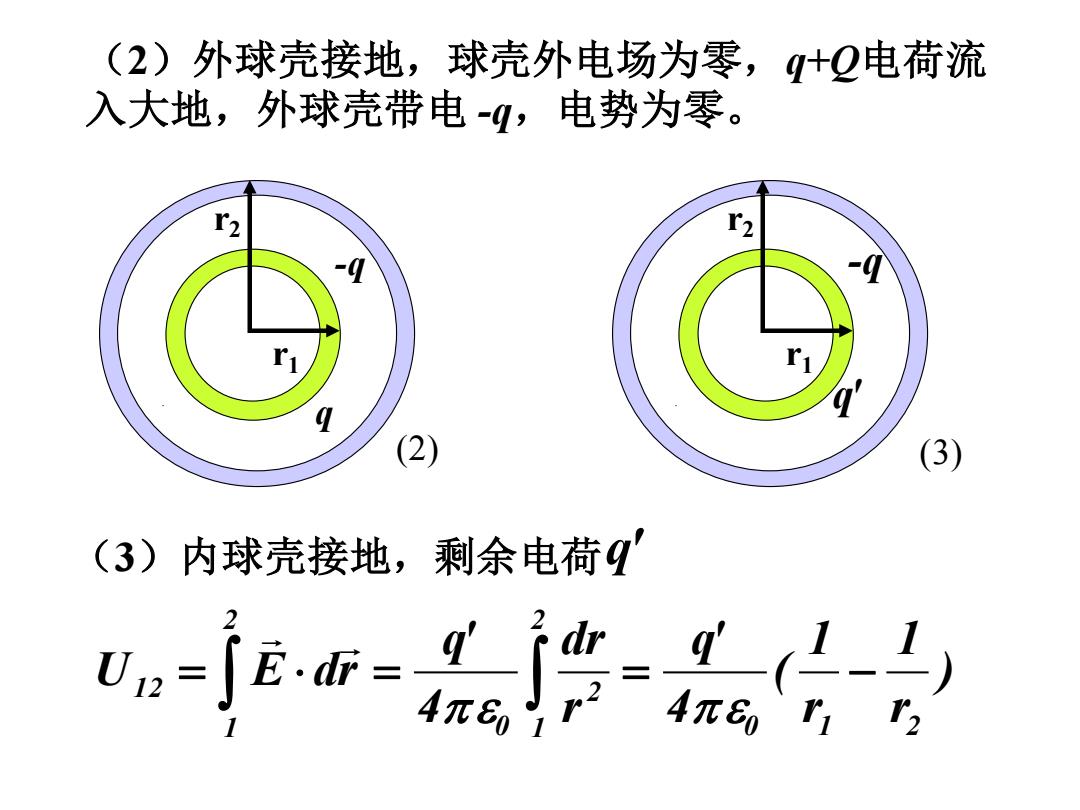
（2）外球壳接地，球壳外电场为零，q+Q电荷流 入大地，外球壳带电 -q，电势为零。 ) r 1 r 1 ( 4 q' r dr 4 q' U E dr 0 1 2 2 1 2 0 2 1 1 2 =  = = −         （3）内球壳接地，剩余电荷 q' r1 r2 q -q (2) r1 r2 -q q' (3)

U2= 9'-9 4π8r2 U1=U12+U2 14-9)=0 4元6 g=q 外球壳电势 (1-9 0→U2=- 2 4π6，r2 内球壳电势 41-1)→0 4元60

0 2 2 4 r q' q U   − = ) 0 r q r q' ( 4 1 U U U 0 1 2 1 12 2 = − = = +   q r r q' 2 1 = 0 2 2 1 2 4 r )q r r ( 1 0 U   − → = − 内球壳电势 ) 0 r 1 r 1 ( 4 q 0 1 2 − →   外球壳电势 r1 r2 -q q

5.一绝缘导体球不带电，距球心r处放一点电荷q, 求导体电势。 解： 导体为等势体，能求得球心0处的电势即可。 导体上感应电荷都在球表面，距球心R U。= q4+ ∑44： 4π6，' 4πEnR 4π8，I' 电荷守恒 ∑q:=0

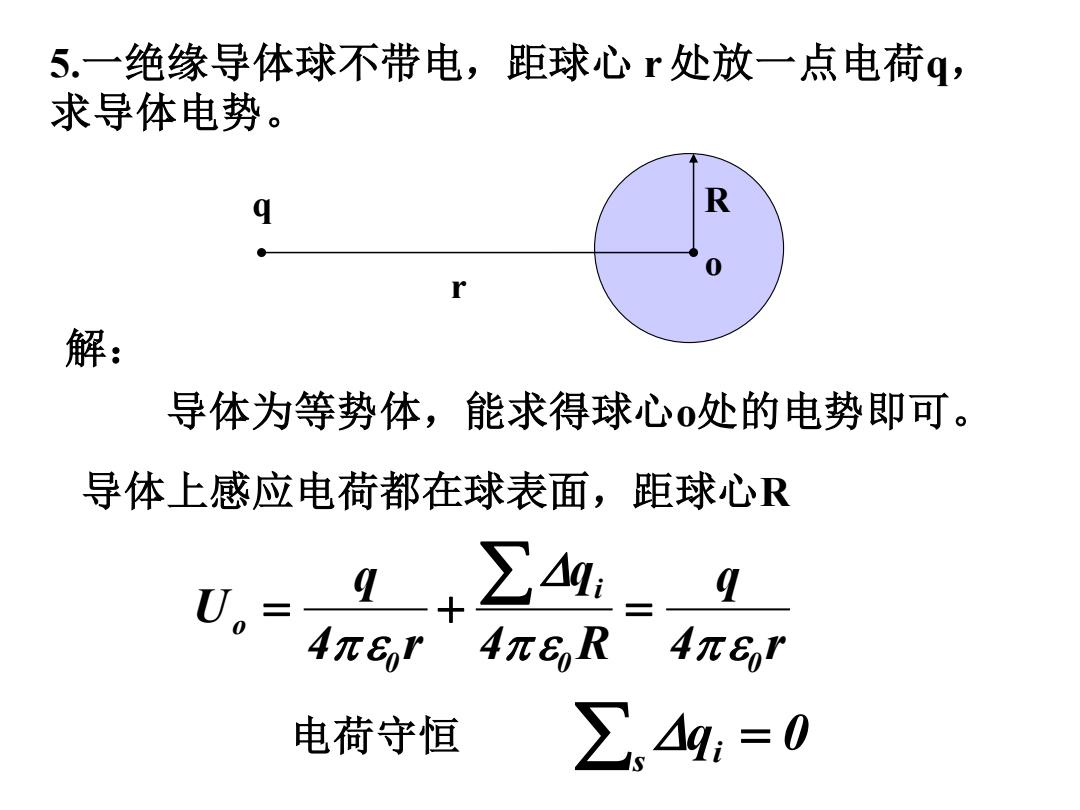
5.一绝缘导体球不带电，距球心 r 处放一点电荷q， 求导体电势。 导体为等势体，能求得球心o处的电势即可。 导体上感应电荷都在球表面，距球心R 4 r q 4 R q 4 r q U 0 0 i 0 o        = +  = 电荷守恒 q 0 s   i = 解： q r o R

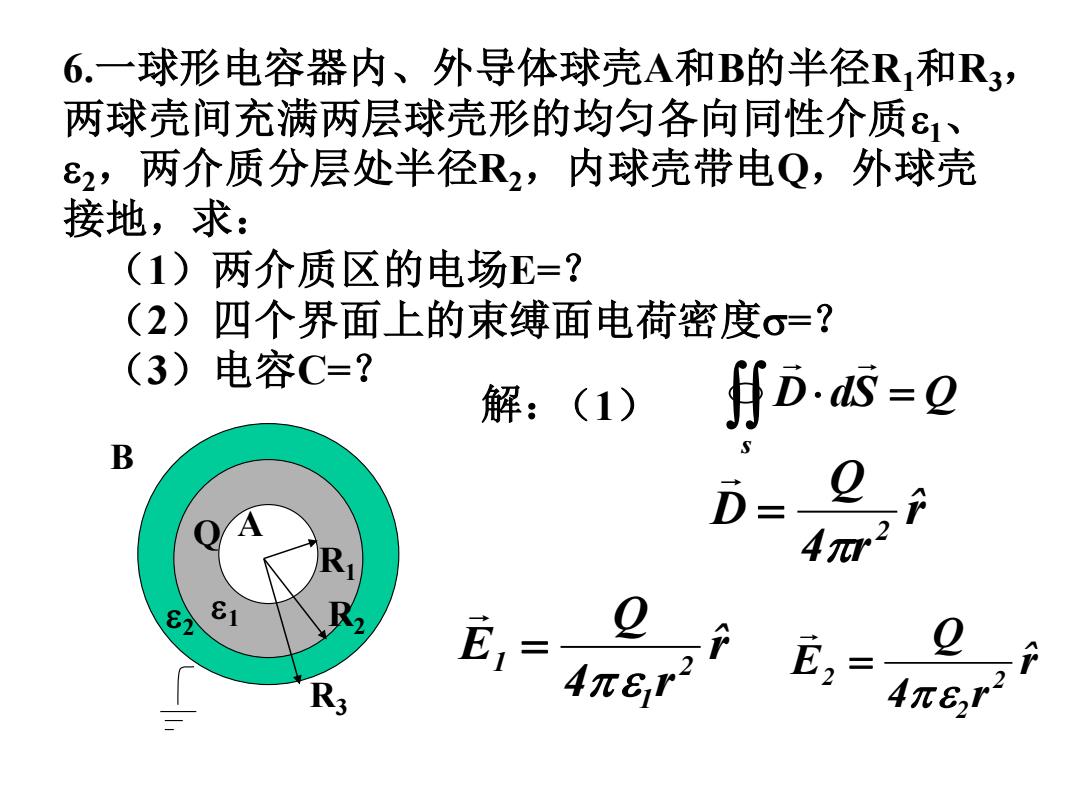
6.一球形电容器内、外导体球壳A和B的半径R和R3, 两球壳间充满两层球壳形的均匀各向同性介质ε、 82,两介质分层处半径R2,内球壳带电Q,外球壳 接地，求： (1)两介质区的电场E=? (2)四个界面上的束缚面电荷密度σ=？ (3)电容C=? 解：(1) f月D.s=e B D= 4m2 81 1二 2 R; AπG令因 4π6，r

6.一球形电容器内、外导体球壳A和B的半径R1和R3， 两球壳间充满两层球壳形的均匀各向同性介质1、 2，两介质分层处半径R2，内球壳带电Q，外球壳 接地，求： （1）两介质区的电场E=？ （2）四个界面上的束缚面电荷密度=？ （3）电容C=？ R3 R2 R1 2 1 A B Q （1）   = s D dS Q   r ˆ 4 r Q D 2  =  rˆ 4 r Q E 2 2 2   =  rˆ 4 r Q E 2 1 1   =  解：

(2) P=(6-8n)E o'=P.i=±(8-6n)E 0, 2(81-80) 4πER1 R3 o,=6-8 4πeR21 2(82-6) 4π6R21 o,=6,-e) 4π6，R3

R3R 2 R 1  2  1 A B Q （ 2 ） P ( 0 ) E   =  −  ' = Pnˆ =  (  −  0 ) E  2 1 1 1 0 1 4 R Q ( ) '      − = − 2 2 3 2 0 4 4 R Q ( ) '      − 2 = 2 2 2 0 3 4 R Q ( ) '      − = − 2 1 2 1 0 2 4 R Q ( ) '      − = 1  ' 2  ' 3  ' 4 

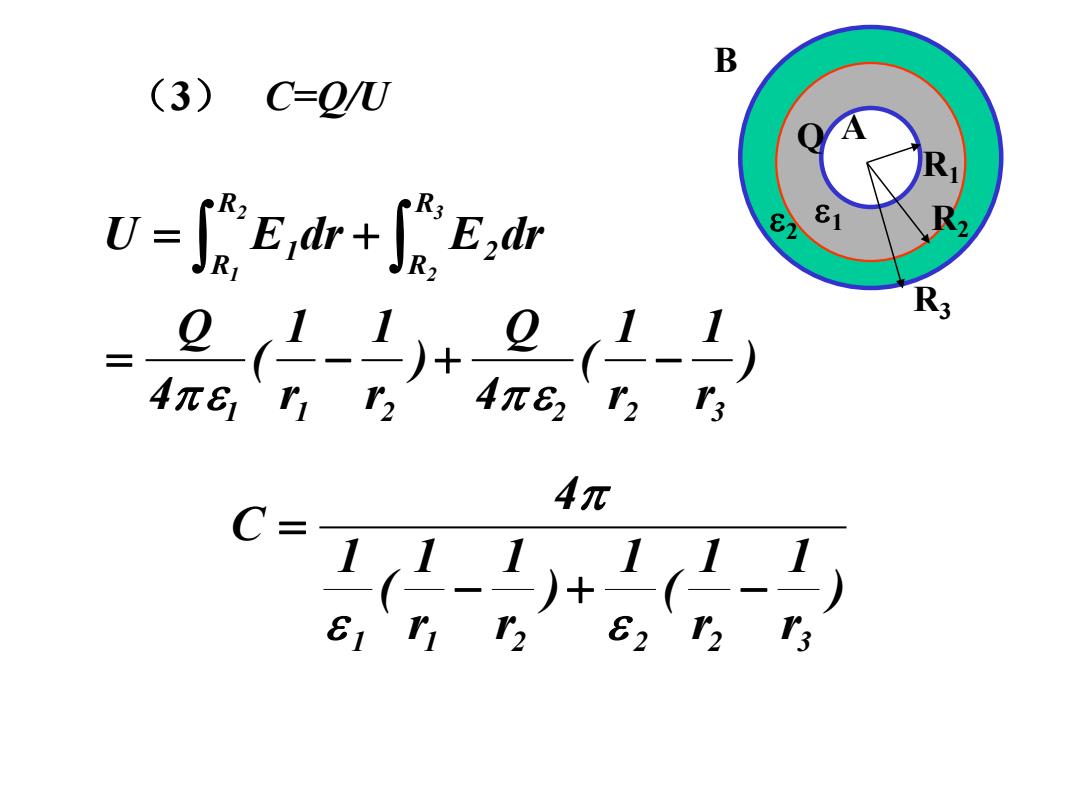
B (3) C=O/U Edr+Edr 82 81 4元 81

（ 3 ） C=Q/U ) r1 r1 ( 4 Q ) r1 r1 ( 4 Q U E dr E dr 1 1 2 2 2 3 RR 2 RR 1 32 21 = − + − = +       ) r1 r1 ( 1 ) r1 r1 ( 1 4 C 1 1 2 2 2 3 − + − =    R3R 2 R 1  2  1 A B Q