
海大理学院教学课件 大学物理学电子教索 循环过程与卡诺循环 6一5理想气体的等温过程和绝热过程 ·等温过程 。 绝热过程 ·绝热线和等温线 6一6循环过程卡诺循环 ·循环过程 卡诺循环
大学物理学电子教案 海大理学院教学课件 循环过程与卡诺循环 6-5 理想气体的等温过程和绝热过程 • 等温过程 • 绝热过程 • 绝热线和等温线 6-6 循环过程 卡诺循环 • 循环过程 • 卡诺循环

复习 热学的研究对象及其分类 气体物态参量 •平衡态与准静态过程 •理想气体的物态方程 功 w-jpar 热量 内能 热力学第一定律 2=△E+W •热力学第一定律在理想气体的等体和等压过程的应用 •摩尔热容 d№v dT P,m dT
复 习 •热学的研究对象及其分类 •气体物态参量 •平衡态与准静态过程 •理想气体的物态方程 •功 2 1 V V W= pdV •热量 •内能 •热力学第一定律 Q = E + W •热力学第一定律在理想气体的等体和等压过程的应用 •摩尔热容 dT dQ C V V ,m = dT dQ C p p,m =

6-5理想气体的等温过程和绝热过程 等温过程 系统从外界 吸收的热量 特点: 全部用来对 理想气体的温度保持不变,T=const 外作功。 过程曲线: 在PV图上是一条双曲线,叫等温线。 过程方程: W,= PV=P2V2 内能、功和热量的变化 pV= RT M dE=0,E=0 Wr- RTIn M Or=Wr= m RTIn m RTIn M M P2
6-5 理想气体的等温过程和绝热过程 一、等温过程 •特点: 理想气体的温度保持不变,T=const •过程曲线: 在PV图上是一条双曲线,叫等温线。 •过程方程: p1 V1 = p2 V2 p V •内能、功和热量的变化 dE = 0, E = 0 = 2 1 V V WT pdVRT M m pV = 1 2 ln V V RT M m WT = 2 1 1 2 ln ln p p RT M m V V RT M m QT =WT = = 系统从外界 吸收的热量, 全部用来对 外作功

绝热过程 1、绝热过程 特点: 系统与外界没有热量交换的过程, Q=0。 内能和功的变化 AE=E,-E=9C亿-T) m W=一 Cn(c,-I) M 特征: 在绝热过程中,系统对外界所作的功是由于系统内能 的减少来完成的
二、绝热过程 1、绝热过程 •特点: 系统与外界没有热量交换的过程, Q=0。 •内能和功的变化 •特征: 在绝热过程中,系统对外界所作的功是由于系统内能 的减少来完成的。 ( ) 2 1 C , T2 T1 M m E = E − E = V m − ( ) C , T2 T1 M m W = − V m −

2、绝热方程 考虑 const Cpm Cv.m =R Kr-IT const p-T-7 const Y=1 p四 推导:对绝热过程,由热力学第一定律 dy d迎 do dE+dw =0 Cv.dT+PdV n 0= M 对于理想气体 dpvr)=0 m pV= RT p const M pdW+Φ=M m RdT 将上式与理想气体的状 态方程结合即可得另外 Cy,mpdV +Cy.mVdp=-RpdV 两式
2、绝热方程 const const const 1 1 = = = − − − p T V T pV 推导:对绝热过程,由热力学第一定律 dQ = dE + dW = 0 C dT PdV M m 0 = V ,m + 对于理想气体 RT M m pV= RdT M m pdV +Vdp= CV ,m pdV + CV ,m Vdp = −RpdV 考虑 CP,m -CV ,m =R V m P m C C , , = p dp V dV = − ( )= 0 d pV= const pV 将上式与理想气体的状 态方程结合即可得另外 两式

绝热过程计算功的方法 将绝热方程pV'=PY?代入W=∫pdW得 w-pYi av = ] ,是-A)
( ) 1 1 2 2 1 2 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 p V p V V p V V V V p V dV V p V W V V − − = − − = − − = = − − − 绝热过程计算功的方法 将绝热方程 代入 得 pV = p1 V1 W = pdV
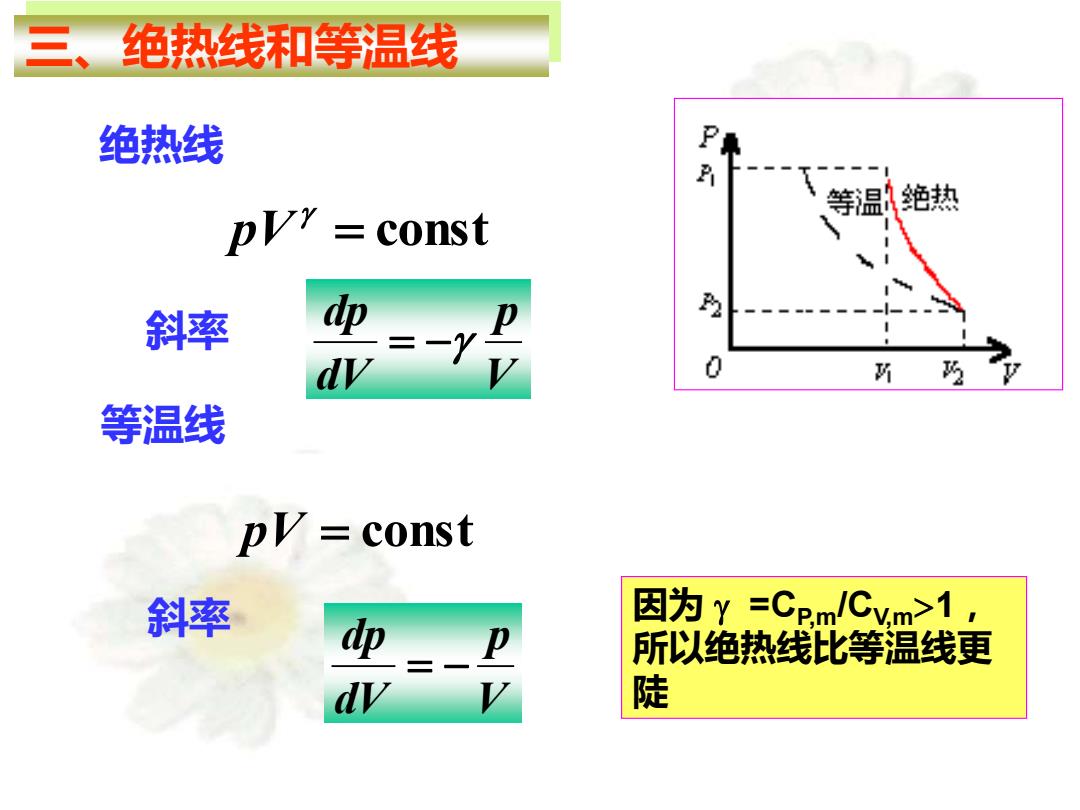
三、绝热线和等温线 绝热线 P 等温 绝热 const 斜率 =-Y &A 等温线 pK=const 斜率 因为Y=Cpm/Cym>1, dp 所以绝热线比等温线更 dy 陡
三、绝热线和等温线 绝热线 = const pV 等温线 pV = const 斜率 V p dV dp = − 斜率 V p dV dp = − 因为 =CP,m/CV,m1, 所以绝热线比等温线更 陡

四、多方过程 P 实际上,气体所进行的过程,常常既 等温绝热 等 不是等温又不是绝热的,而是介于两 者之间,可表示为 P=常量 (n为多方指数) 等压 凡满足上式的过程称为多方过程。 n=1 等温过程 n =Y 绝热过程 说明: n=0 等压过程 理想气体的内能增量为 n =oo 一等容过程 一般情况1<n<Y,多方过程可近似 △E= Cv.AT M 代表气体内进行的实际过程。 理想气体的状态方程 对各种过程都成立
四、多方过程 实际上,气体所进行的过程,常常既 不是等温又不是绝热的,而是介于两 者之间,可表示为 PVn =常量 (n为多方指数) 凡满足上式的过程称为多方过程。 n =1 —— 等温过程 n = —— 绝热过程 n= 0 —— 等压过程 n = —— 等容过程 一般情况1 n ,多方过程可近似 代表气体内进行的实际过程。 说明: 理想气体的内能增量为 C T M m E = V ,m 理想气体的状态方程 对各种过程都成立
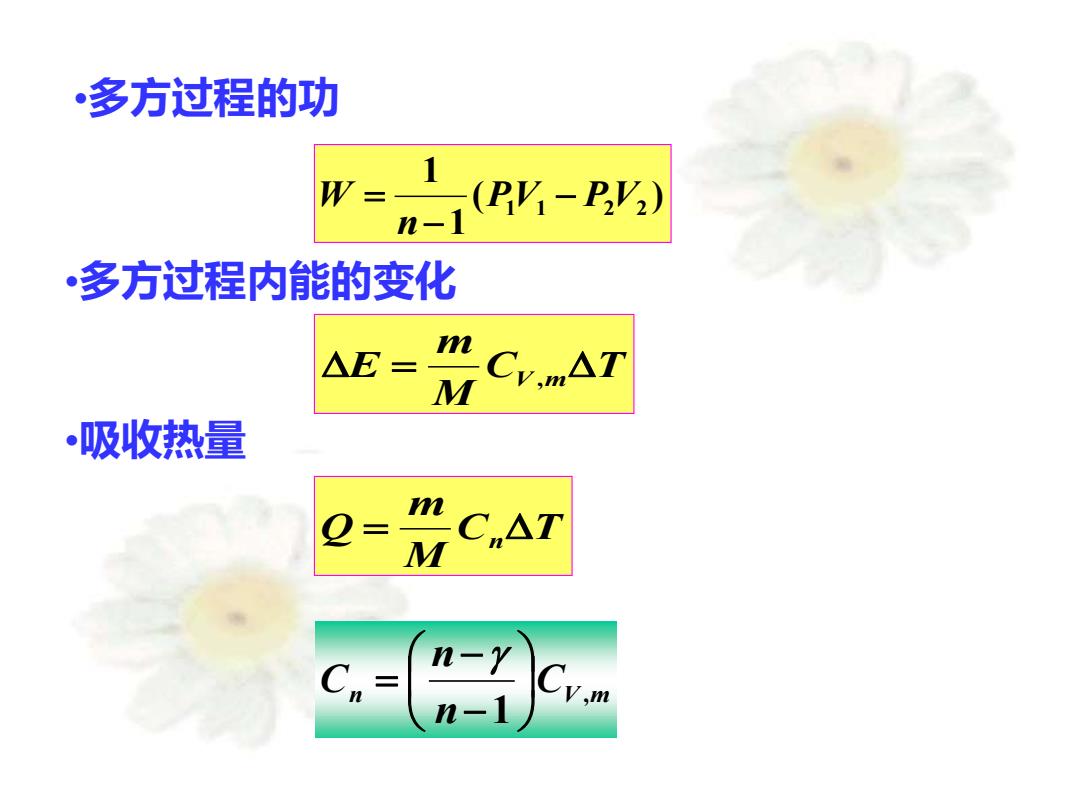
多方过程的功 (PK-PV) n-] 多方过程内能的变化 AE= n M 吸收热量 Cn△T M /,m
•多方过程的功 ( ) 1 1 P1 V1 P2 V2 n W − − = C T M m E = V ,m n CV m n n C , 1 − − = •吸收热量 •多方过程内能的变化 C T M m Q = n

6-6循环过程 卡诺循环 循环过程 在热机中被用来吸收热量并对外作功的物质叫工作物 质,简称工质。工质往往经历着循环过程,即经历一 系列变化又回到初始状态。 1、定义: 系统经过一系列状态变化以后,又回到原 来状态的过程叫作热力学系统的循环过程, 简称循环。 2、特点: ·若循环的每一阶段都是准静态过程,则此循环可 用P-V图上的一条闭合曲线表示。工质在整个循环 过程中对外作的净功等于曲线所包围的面积。 ·系统经过一个循环以后,系统的内能没有变化
在热机中被用来吸收热量并对外作功的物质叫工作物 质,简称工质。工质往往经历着循环过程,即经历一 系列变化又回到初始状态。 2、特点: •若循环的每一阶段都是准静态过程,则此循环可 用P-V图上的一条闭合曲线表示。工质在整个循环 过程中对外作 的净功等于曲线所包围的面积。 •系统经过一个循环以后,系统的内能没有变化 6-6 循环过程 卡诺循环 一、循环过程 1、定义: 系统经过一系列状态变化以后,又回到原 来状态的过程叫作热力学系统的循环过程, 简称循环