广东海洋大学：《大学物理》课程教学资源（习题分析与解答）第十三章 电磁感应（1/2）

第中章习國戴分新解器

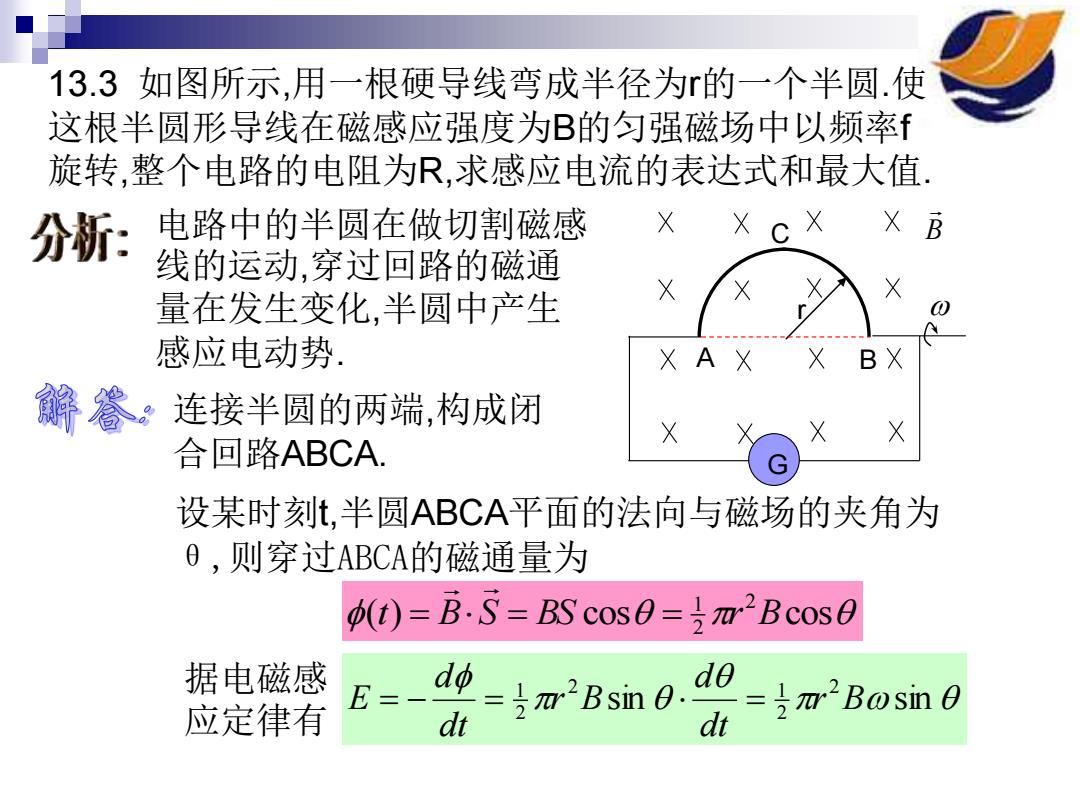
13.3如图所示，用一根硬导线弯成半径为r的一个半圆.使 这根半圆形导线在磁感应强度为B的匀强磁场中以频率f 旋转，整个电路的电阻为R,求感应电流的表达式和最大值 分所： 电路中的半圆在做切割磁感 X cX X B 线的运动，穿过回路的磁通 量在发生变化，半圆中产生 感应电动势 A BX 解餐 连接半圆的两端，构成闭 合▣路ABCA 设某时刻t,半圆ABCA平面的法向与磁场的夹角为 0,则穿过ABCA的磁通量为 (t)=B·S=BS cos0=号m2Bcos0 据电磁感 E= dφ 应定律有 dt =号m2Bsm0.d0 2x2Bosin 0

13.3 如图所示,用一根硬导线弯成半径为r的一个半圆.使 这根半圆形导线在磁感应强度为B的匀强磁场中以频率f 旋转,整个电路的电阻为R,求感应电流的表达式和最大值. r  B  G 电路中的半圆在做切割磁感 线的运动,穿过回路的磁通 量在发生变化,半圆中产生 感应电动势. 连接半圆的两端,构成闭 合回路ABCA. A B C 设某时刻t,半圆ABCA平面的法向与磁场的夹角为 θ,则穿过ABCA的磁通量为 ( ) cos  cos 2 2 1 t = BS = BS = r B   据电磁感 应定律有        sin sin 2 2 2 1 2 1 r B dt d r B dt d E = − =  =

若设初始时刻，半圆ABCA平面的法向与磁场的夹角为0， 即回路的环绕方向为顺时针(A→B→C→A).则 0=ot =2nft 而对闭合回路ABCA来说，辅助线AB不产生电动势.于是 得到半圆中产生的电动势即为 E=π2r2 Bf sin(2dt) 易知电路中的 Eπ2r2 Bf sin(2i) 感应电流为 R R 可见电路的电流随时间做正弦变化.在图中位置时，电流 沿顺时针.感应电流的最大值为 m =π2r2Bf/R

若设初始时刻,半圆ABCA平面的法向与磁场的夹角为0, 即回路的环绕方向为顺时针(A→B →C →A).则  =t = 2ft 而对闭合回路ABCA来说,辅助线AB不产生电动势.于是 得到半圆中产生的电动势即为 sin( 2 ) 2 2 E =  r Bf ft 易知电路中的 感应电流为 R r Bf ft R E I sin( 2 ) 2 2   = = 可见电路的电流随时间做正弦变化.在图中位置时,电流 沿顺时针.感应电流的最大值为 I m r Bf R 2 2 = 

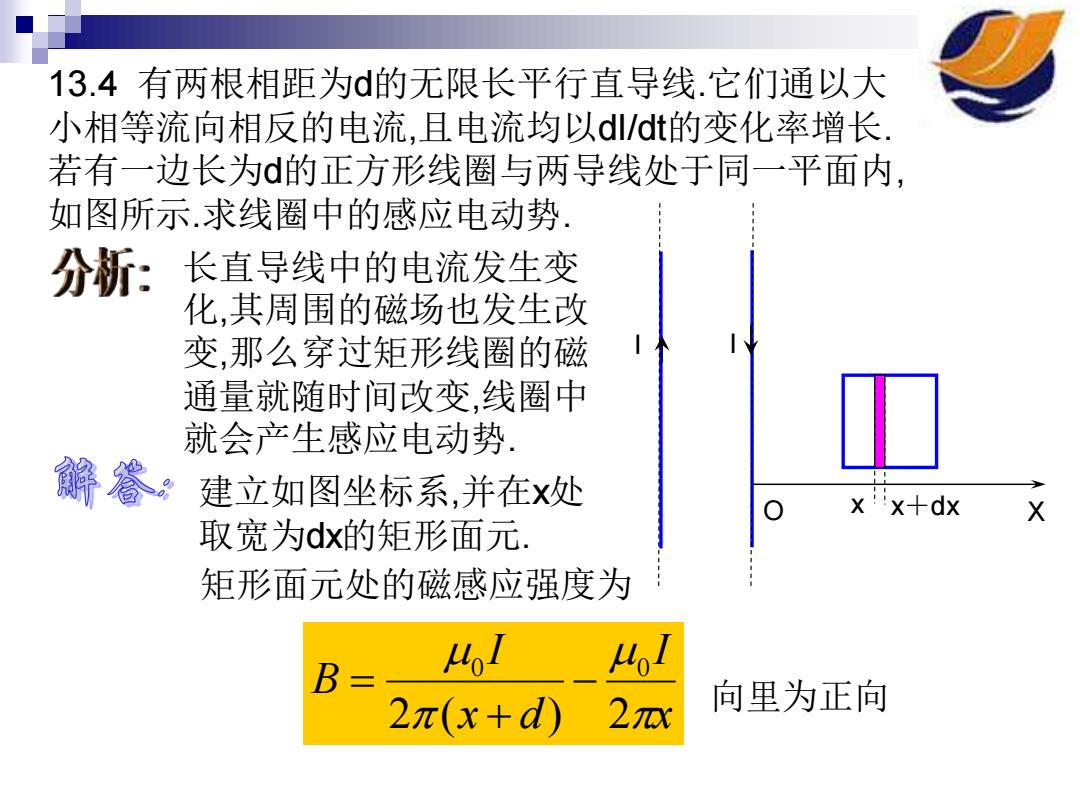
13.4有两根相距为d的无限长平行直导线.它们通以大 小相等流向相反的电流，且电流均以d/t的变化率增长 若有一边长为d的正方形线圈与两导线处于同一平面内， 如图所示求线圈中的感应电动势 分新：长直导线中的电流发生变 化，其周围的磁场也发生改 变，那么穿过矩形线圈的磁 通量就随时间改变，线圈中 就会产生感应电动势， 解眷 建立如图坐标系，并在x处 X'x+dx 取宽为dx的矩形面元 矩形面元处的磁感应强度为 B 41 2π(x+d) 2 向里为正向

13.4 有两根相距为d的无限长平行直导线.它们通以大 小相等流向相反的电流,且电流均以dI/dt的变化率增长. 若有一边长为d的正方形线圈与两导线处于同一平面内, 如图所示.求线圈中的感应电动势. O X I I x x＋dx 长直导线中的电流发生变 化,其周围的磁场也发生改 变,那么穿过矩形线圈的磁 通量就随时间改变,线圈中 就会产生感应电动势. 建立如图坐标系,并在x处 取宽为dx的矩形面元. 矩形面元处的磁感应强度为 x I x d I B     2 ( ) 2 0 0 − + = 向里为正向

若取矩形面元的法向也向里.则穿过面元的磁通量为 d中=Bdk= 41 4 d.dx 2π(x+d) 2 穿过整个矩形回路的磁通量为 3 d.dx= 2π(x+d) 2 2π 根据电磁感应定律得到 d dt 2 电动势为正，说明与矩形平面法向成右手螺旋关系，即沿顺 时针.当然也可根据楞次定律来判断！

若取矩形面元的法向也向里.则穿过面元的磁通量为 d dx x I x d I d B ds         − + =  =      2 ( ) 2 0 0  穿过整个矩形回路的磁通量为 4 3 ln 2 ( ) 2 2 0 2 0 0         Id d dx x I x d I d d d   =       − + = =   根据电磁感应定律得到 dt d dI dt d E       = − = 3 4 ln 2 0    电动势为正,说明与矩形平面法向成右手螺旋关系,即沿顺 时针.当然也可根据楞次定律来判断

13.7如图所示，把一半径为R的半圆形导线OP置于磁感 强度为B的均匀磁场中，当导线以速率V水平向右平动时， 求导线中感应电动势的大小，哪一端电势高？ 解誊建立如图坐标系，并在导线上 取线元dd,其产生的电动势为 Y个立×B de=(xB)dl 由于线元运动方向与磁场垂直，而 二者叉乘方向沿Y轴，所以得到 ds=vBal cos0=vBcos ORde X 整个半圆导体中产生的电动势为 ds= vBcos ORd0 =2RvB EoP为正，说明电动势方向从O指向P,即P端电势较高

13.7 如图所示,把一半径为R的半圆形导线OP置于磁感 强度为B的均匀磁场中,当导线以速率v水平向右平动时, 求导线中感应电动势的大小,哪一端电势高? R O O X Y v   dθ P v B     dl  建立如图坐标系,并在导线上 取线元 dl ,其产生的电动势为  d (v B) dl     =  • 由于线元运动方向与磁场垂直,而 二者叉乘方向沿Y轴,所以得到 d = vBdl cos = vBcosRd 整个半圆导体中产生的电动势为  −  = = = 2 2 cos 2   d v B Rd RvB P O OP EOP为正,说明电动势方向从O指向P,即P端电势较高

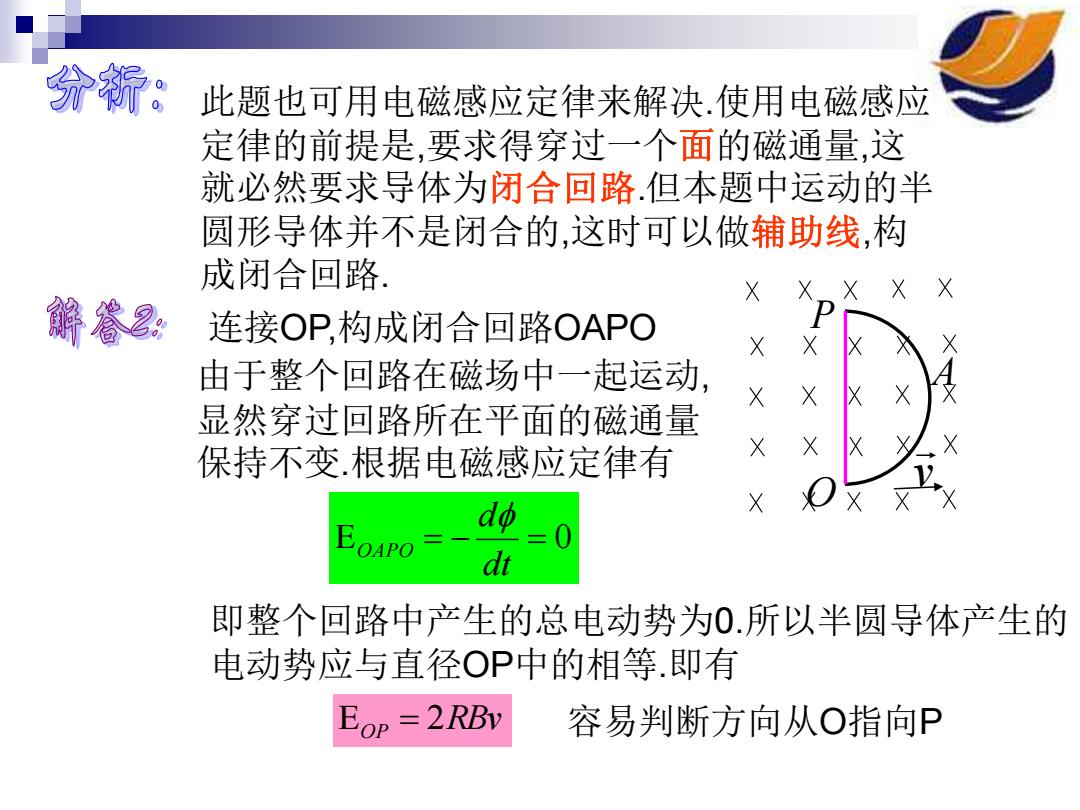
分舒。 此题也可用电磁感应定律来解决.使用电磁感应 定律的前提是，要求得穿过一个面的磁通量，这 就必然要求导体为闭合回路但本题中运动的半 圆形导体并不是闭合的，这时可以做辅助线，构 成闭合回路， X XXXX 解誉 连接OP,构成闭合回路OAPO 由于整个回路在磁场中一起运动， 显然穿过回路所在平面的磁通量 保持不变根据电磁感应定律有 dΦ EOAPO dt 即整个回路中产生的总电动势为0.所以半圆导体产生的 电动势应与直径OP中的相等.即有 EOP =2RBv 容易判断方向从O指向P

此题也可用电磁感应定律来解决.使用电磁感应 定律的前提是,要求得穿过一个面的磁通量,这 就必然要求导体为闭合回路.但本题中运动的半 圆形导体并不是闭合的,这时可以做辅助线,构 成闭合回路. v  O 连接OP,构成闭合回路OAPO P 由于整个回路在磁场中一起运动, A 显然穿过回路所在平面的磁通量 保持不变.根据电磁感应定律有  = − = 0 dt d OAPO  即整个回路中产生的总电动势为0.所以半圆导体产生的 电动势应与直径OP中的相等.即有 RBv OP = 2 容易判断方向从O指向P

13.9如图所示，长为L的导体棒OP,处于均匀磁场中，并绕 OO轴以角速度ω旋转，棒与转轴间夹角恒为0，磁感强 度B与转轴平行.求OP棒在图示位置处的电动势. 解誉：在导体棒OP上取线元 其中产生的 电动势为 de =(ixB)dl 而由图示可知，线元运动方向与磁场垂直， 二者叉乘方向与转轴垂直.所以 ds vBdl cosa =oBsin2Oldl 导体棒OP上产生的电动势为 EoP为正值，说明电动势方向由O指向P,即P端电势较高！

13.9 如图所示,长为L的导体棒OP,处于均匀磁场中,并绕 OO′轴以角速度ω旋转,棒与转轴间夹角恒为θ ,磁感强 度B与转轴平行.求OP棒在图示位置处的电动势. B  O Q P   v B     在导体棒OP上取线元 其中产生的 电动势为 d (v B) dl     =  • 而由图示可知,线元运动方向与磁场垂直, 二者叉乘方向与转轴垂直.所以 d vBdl  B ldl 2 = cos = sin 导体棒OP上产生的电动势为 ( ) 2 0 2 sin 2 1 d Bsin ldl B L  P L O O P    = = = EOP为正值,说明电动势方向由O指向P,即P端电势较高. l lsin dl 

解眷 此问题也可用电磁感应定律来 解决.做辅助线构成OPQO闭合 B 回路 由于闭合回路OPQO所在平面始终与 磁场平行（平面法向与磁场垂直），所以 0 由电磁感应定律知，闭合回路OPQO中的 感应电动势为0.即 dφ EoPQo =0 dt 即有 Eop +Epe+Eoo=0 所以 Eop=-Epo=Bo(Lsin e)2

B  O Q P   此问题也可用电磁感应定律来 解决.做辅助线构成OPQO闭合 回路. 由于闭合回路OPQO所在平面始终与 磁场平行(平面法向与磁场垂直),所以   0 由电磁感应定律知,闭合回路OPQO中的 感应电动势为0.即  = − = 0 dt d OPQO  即有 EOP + EPQ + EQO = 0 2 2 1 E E B(Lsin ) 所以 OP = − PQ = O Q P

13.10如图所示，金属杆AB以匀速v=2.0m/s平行于一长 直导线移动，此导线通有电流=40A.问：此杆中的感应电 动势为多大？哪一端的电势高？ 解春 建立如图坐标系，并在导体棒 AB上取线元 dl dxi 其中所产生的电动势为 币XB de=6×Bdi 根据图示， 可以得到 de=v Bdx cosπ=-vBdk A B dx 又因为 所以 Ea=--0=-n11=-384×10 2元 EAB为负值，说明电动势方向由B指向A,即A端电势较高

13.10 如图所示,金属杆AB以匀速v=2.0m/s平行于一长 直导线移动,此导线通有电流I=40A.问:此杆中的感应电 动势为多大?哪一端的电势高? I v  A B dx v B    O X 建立如图坐标系,并在导体棒 AB上取线元 dl dxi   = 其中所产生的电动势为 d (v B) dl     =   根据图示, 可以得到 d = vBdxcos = −vBdx 又因为 x I B   2 0 = 所以 V Iv dx x I E vBdx v B A A B 0 5 1.1 0.1 0 ln 11 3.84 10 2 2 − = − = − = − = −        EAB为负值,说明电动势方向由B指向A,即A端电势较高