
第九章静电场中的导体和介质分习题分析与解答 第克章都粉司题桥锦容
第九章 静电场中的导体和介质部分习题分析与解答
第九章 静电场中的导体和介质部分习题分析与解答 9-3 在一半径为R=6.0cm的金属球A外面套有一个同 心的金属球壳B,已知球壳B的内、外半径分别为 R2=8.0cm,R3=10.0cm.设球A带有总电荷QA=3.0×10-8C 球壳B带有总电荷Q=2.0×108C.(1)求球壳B内、外 表面上所带的电荷以及球A和球壳B的电势;(2)将球 壳B接地然后断开,再把金属球A接地,求金属球A和球 壳B内、外表面上所带的电荷以及球A和球壳B的电势。 R QA -Qa QA+Q分
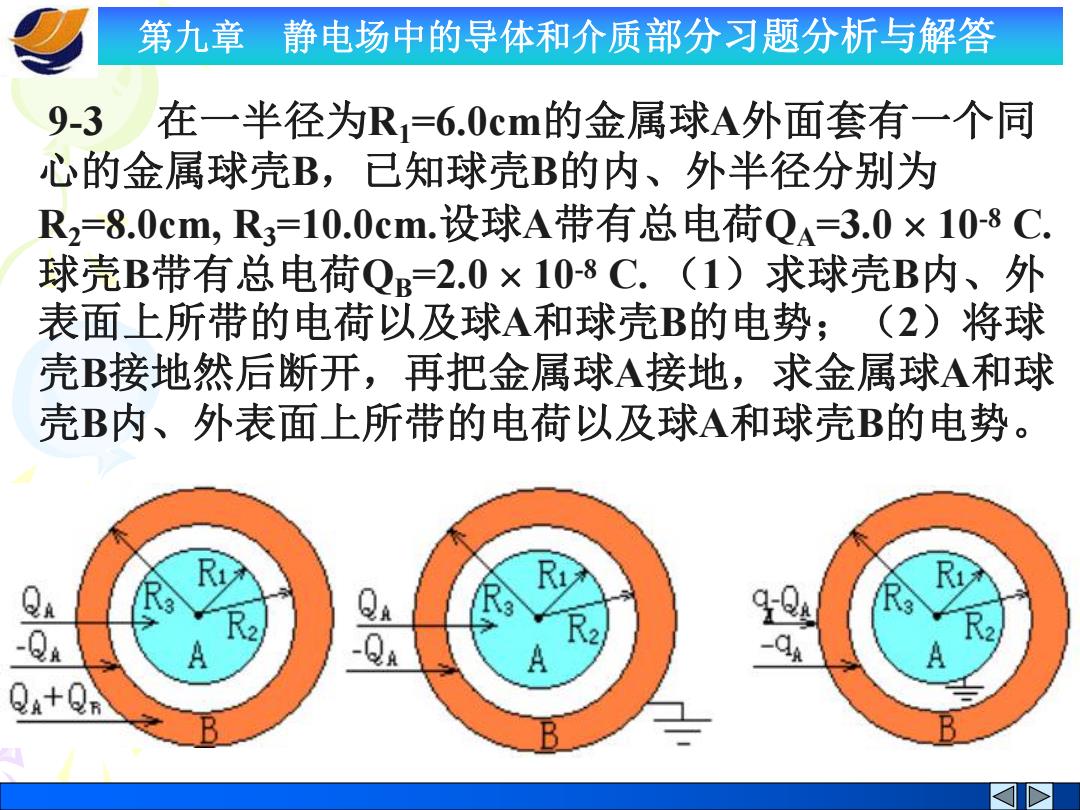
第九章 静电场中的导体和介质部分习题分析与解答 9-3 在一半径为R1=6.0cm的金属球A外面套有一个同 心的金属球壳B,已知球壳B的内、外半径分别为 R2=8.0cm, R3=10.0cm.设球A带有总电荷QA=3.0 10 -8 C. 球壳B带有总电荷QB=2.0 10 -8 C. (1)求球壳B内、外 表面上所带的电荷以及球A和球壳B的电势;(2)将球 壳B接地然后断开,再把金属球A接地,求金属球A和球 壳B内、外表面上所带的电荷以及球A和球壳B的电势

第九章静电场中的导体和介质部分习题分析与解答 解:(1)由于静电平衡时电荷只分布于导体的表面上, 故:球A在外表面带电Q4=3.0×108C,球壳B内表面 带电-Q4=-3.0×10-8C,球壳B外表面带电Q4+QB=5.0 ×10-8C。 由电势的叠加,知球A和球壳B的电势分别为: 0 VA=4πGR +-04+24+0B=5.6×103y 4πER24πER Va= 2+2 2=4.5×103V 4π6R (2)将球壳B接地后断开,再把球A接地,设球A带电 qA,球A和球壳B的电势为:
第九章 静电场中的导体和介质部分习题分析与解答 解: (1)由于静电平衡时电荷只分布于导体的表面上, 故:球A在外表面带电QA=3.0 10 -8 C,球壳B内表面 带电-QA= -3.0 10 -8 C,球壳B外表面带电QA + QB = 5.0 10 -8 C。 由电势的叠加,知球A和球壳B的电势分别为: V R Q Q R Q R Q V A A A B A 3 0 1 0 2 0 3 5.6 10 4 4 4 V R Q Q V A B B 3 0 3 4.5 10 4 (2) 将球壳B接地后断开,再把球A接地,设球A带电 qA,球A和球壳B的电势为:

第九章 静电场中的导体和介质部分习题分析与解答 -q 4+-4+94=0 4π6R14π6R 。4π8R 4πER3 RRO 解得:q4=RR,+RR-RB =2.12×10-8C 得:ya=-,+44=-792×102T 4π8oR3 即,球A的外表面、球壳B的内、外表面所带的电荷 分别为:2.12×10-8C、-2.12×10-8C、-0.9×10-8C
第九章 静电场中的导体和介质部分习题分析与解答 0 4 4 4 0 1 0 2 0 3 R Q q R q R q V A A A A A 0 3 4 R Q q V A A B C R R R R R R R R Q q A A 8 1 2 2 3 1 3 1 2 2.12 10 解得: V R Q q V A A B 2 0 3 7.92 10 4 得: 即,球A的外表面、球壳B的内、外表面所带的电荷 分别为:2.1210 -8 C、 -2.1210 -8 C、 -0.910 -8 C
第九章静电场中的导体和介质部分习题分析与解答 9-4三个平行板A、B和C的面积均为S,其中A板带 电Q,B、C板不带电,A、B间相距为d1,A、C间相 距为d2。求:(1)各导体板上的电荷分布和导体板间 的电势差;(2)将B、C两导体板分别接地,再求导 体板上的电荷分布和导体板间的电势差。 B C aci Acr 0 BL 4BR
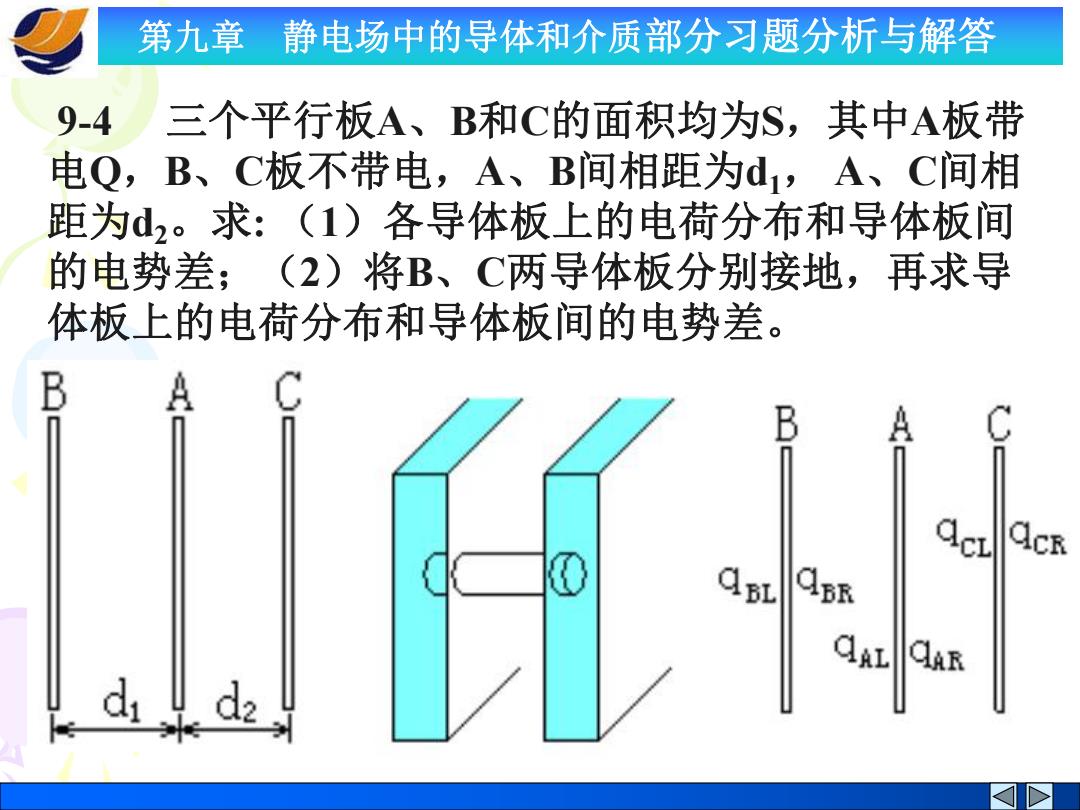
第九章 静电场中的导体和介质部分习题分析与解答 9-4 三个平行板A、B和C的面积均为S,其中A板带 电Q,B、C板不带电,A、B间相距为d1, A、C间相 距为d2。求: (1)各导体板上的电荷分布和导体板间 的电势差;(2)将B、C两导体板分别接地,再求导 体板上的电荷分布和导体板间的电势差

第九章 静电场中的导体和介质部分习题分析与解答 解:(1)设电荷分布如上图所示,据静电平衡时导体 板上电荷分布的规律,有 由高斯定理知: BL=4CR QBR-QAL QAR=-qCL 又对导体板B:qBL+qBR=O 对导体板C:qcL+qcR=0 对导体板A:qAL+qAR=Q 联立以上各式,得qBL=qAL=qAR=qCR=Q/2 9BR=QCL=-Q/2
第九章 静电场中的导体和介质部分习题分析与解答 解:(1)设电荷分布如上图所示,据静电平衡时导体 板上电荷分布的规律,有 由高斯定理知:qBL = qCR qBR =- qAL qAR =- qCL 又对导体板B:qBL + qBR =0 对导体板C:qCL + qCR =0 对导体板A:qAL + qAR =Q 联立以上各式,得 qBL = qAL= qAR = qCR =Q/2 qBR = qCL=-Q/2

第九章静电场中的导体和介质部分习题分析与解答 故有:V刷= -d 26S VAc= 26S (2)B、C两导体接地,UBc=0,则有 ABL=qCR=0 QAR+gAL=Q BR=-GAL OCL=-QAR 4BRd-d2 EoS EoS
第九章 静电场中的导体和介质部分习题分析与解答 1 0 2 d S Q VBA 故有: 2 2 0 d S Q VAC (2)B、C两导体接地,UBC=0,则有 qBL = qCR=0 qAR+ qAL =Q qBR =- qAL qCL =- qAR 2 0 0 1 0 d S q d S qBR CL

第九章 静电场中的导体和介质部分习题分析与解答 联立以上各式,得 9R=4=- d d +dz d qci.=-9iR =d+dz UBA=- ddz Q eoS d +d, Uic= o dd, &oS d +d
第九章 静电场中的导体和介质部分习题分析与解答 联立以上各式,得 Q d d d q q BR AL 1 2 2 Q d d d q q CL AR 1 2 1 1 2 1 2 0 d d d d S Q UBA 1 2 1 2 0 d d d d S Q UAC

第九章静电场中的导体和介质部分习题分析与解答 9-6在真空中,将半径为R的金属球接地,与球心 O相距为r(>R)处放置一点电荷q,不计接地导线上 电荷的影响。求金属球表面上的感应电荷总量。 解:金属球为等势体,金属 球上任一点的电势V等于点电 荷q和金属球表面感应电荷q' 在球心处激发的电势之和。 而金属球接地,总电势为零。 所以球心处的电势为 V= 9 dq" 十Js4G 4π8o1 感应电荷总量为:q=、dg=- R
第九章 静电场中的导体和介质部分习题分析与解答 9-6 在真空中,将半径为R的金属球接地,与球心 O相距为r(r>R)处放置一点电荷q,不计接地导线上 电荷的影响。求金属球表面上的感应电荷总量。 q q’ R O r 解:金属球为等势体,金属 球上任一点的电势V等于点电 荷q和金属球表面感应电荷q’ 在球心处激发的电势之和。 而金属球接地,总电势为零。 所以球心处的电势为 S S dq r R q R dq r q V 0 4 1 4 0 4 0 4 0 0 感应电荷总量为: q r R q dq S

第九章 静电场中的导体和介质部分习题分析与解答 9-8 两根输电线,其导线半径为3.26mm,两线中心 相距0.50m,线位于地面上空很高处,因而大地的影 响可以忽略。求输电线单位长度的电容。 解:由课本第九章9-2节例3可知两输电线的电势差 U= d-R πE0 R 因此,输电线单位长度的电容为 πe0 IEo U d-R Ind/R In R 代入数据,得 C=4.86×10-12uF
第九章 静电场中的导体和介质部分习题分析与解答 9-8 两根输电线,其导线半径为3.26mm,两线中心 相距0.50m,线位于地面上空很高处,因而大地的影 响可以忽略。求输电线单位长度的电容。 解:由课本第九章9-2节例3可知两输电线的电势差 R d R U ln 0 因此,输电线单位长度的电容为 d R R U d R C ln / ln 0 0 代入数据,得 C F 12 4.86 10