
一海大理学院表号课件 大学物理学电子教案 刚体的转动(1) 4-1刚体的定轴转动 4-2力矩转动定律转动惯量(上) ·力矩 ·转动定律 转动惯量
大学物理学电子教案 海大理学院教学课件 刚体的转动(1) 4-1 刚体的定轴转动 4-2 力矩 转动定律 转动惯量(上) • 力矩 • 转动定律 • 转动惯量
第四章 刚体的转动 引言 物体的形状和大小不发生变化,即物体内任意两 点之间的距离都保持不变—刚体。 说明 1)理想化的力学模型; 2)任何两点之间的距离在运动过程中保持不变: 3)刚体可以看成是无数质点组成的质点系 刚体可以看成一个包含由大量质点、而各个质点间距离保持不变 的质点系
第四章 刚体的转动 引言 物体的形状和大小不发生变化,即物体内任意两 点之间的距离都保持不变——刚体。 说明 1) 理想化的力学模型; 2) 任何两点之间的距离在运动过程中保持不变; 3)刚体可以看成是无数质点组成的质点系 刚体可以看成一个包含由大量质点、而各个质点间距离保持不变 的质点系
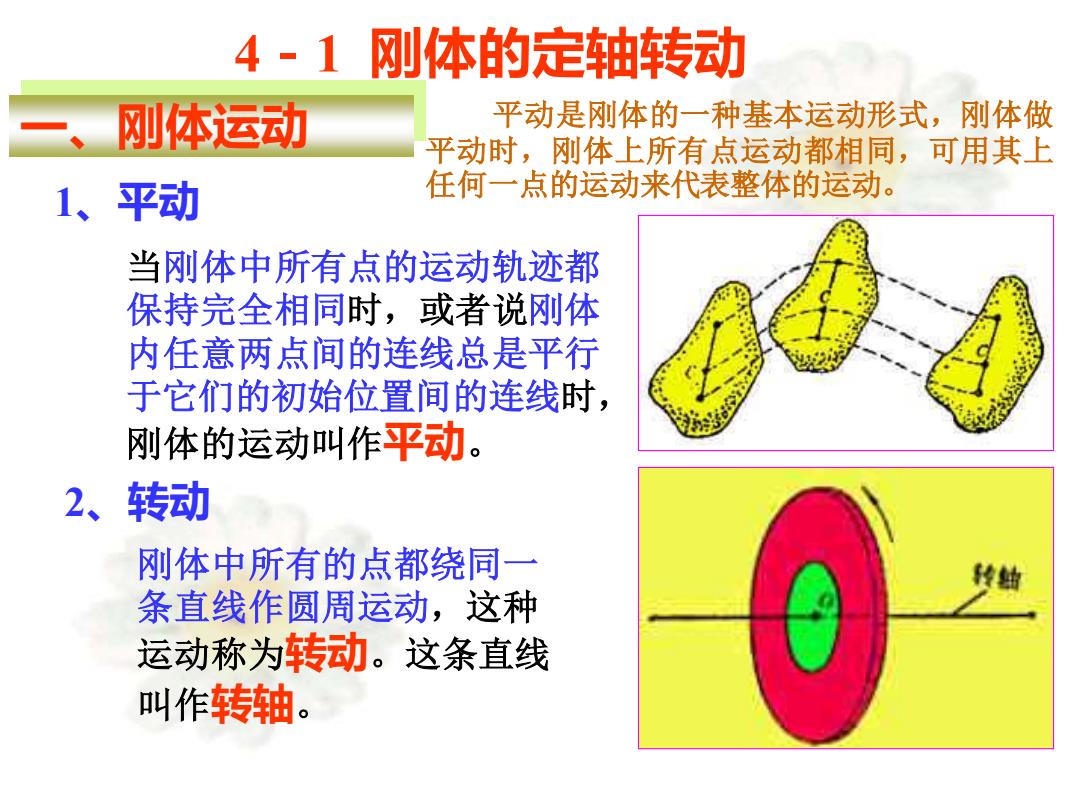
4-1刚体的定轴转动 刚体运动 平动是刚体的一种基本运动形式,刚体做 平动时,刚体上所有点运动都相同,可用其上 1、 平动 任何一点的运动来代表整体的运动。 当刚体中所有点的运动轨迹都 保持完全相同时,或者说刚体 内任意两点间的连线总是平行 于它们的初始位置间的连线时, 刚体的运动叫作平动。 2、转动 刚体中所有的点都绕同一 条直线作圆周运动,这种 运动称为转动。这条直线 叫作转轴
4-1 刚体的定轴转动 一、刚体运动 1、平动 当刚体中所有点的运动轨迹都 保持完全相同时,或者说刚体 内任意两点间的连线总是平行 于它们的初始位置间的连线时, 刚体的运动叫作平动。 2、转动 刚体中所有的点都绕同一 条直线作圆周运动,这种 运动称为转动。这条直线 叫作转轴。 平动是刚体的一种基本运动形式,刚体做 平动时,刚体上所有点运动都相同,可用其上 任何一点的运动来代表整体的运动
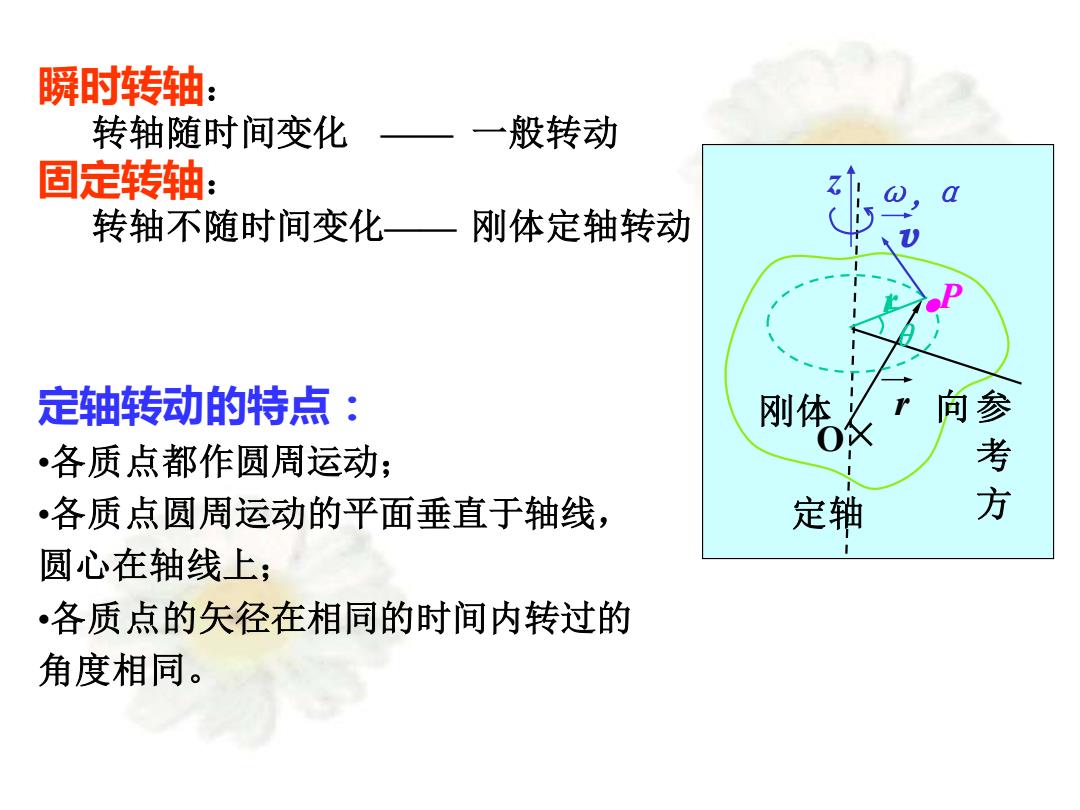
瞬时转轴: 转轴随时间变化 一般转动 固定转轴: 转轴不随时间变化, 刚体定轴转动 定轴转动的特点: 向参 •各质点都作圆周运动; 刚体 各质点圆周运动的平面垂直于轴线, 定轴 方 圆心在轴线上; 各质点的矢径在相同的时间内转过的 角度相同
瞬时转轴: 转轴随时间变化 —— 一般转动 固定转轴: 转轴不随时间变化—— 刚体定轴转动 定轴转动的特点: •各质点都作圆周运动; •各质点圆周运动的平面垂直于轴线, 圆心在轴线上; •各质点的矢径在相同的时间内转过的 角度相同。 O v P × ω,α r r 定轴 刚体 • 参 考 方 向 θ z

B' 3、刚体的一般运动 一个汽车轮子在地 上的滚动 A、B、C、各点的 运动都不相同 B →0轮子的平种 列体的运动=平动十转动 A 绕过0轴的转动
3、刚体的一般运动 一个汽车轮子在地 上的滚动 A、B、C、…各点的 运动都不相同 绕过o 轴的转动 o A B C o→ o轮子的平动 A B C o A B C o A B A B C C o 刚体的运动=平动+转动
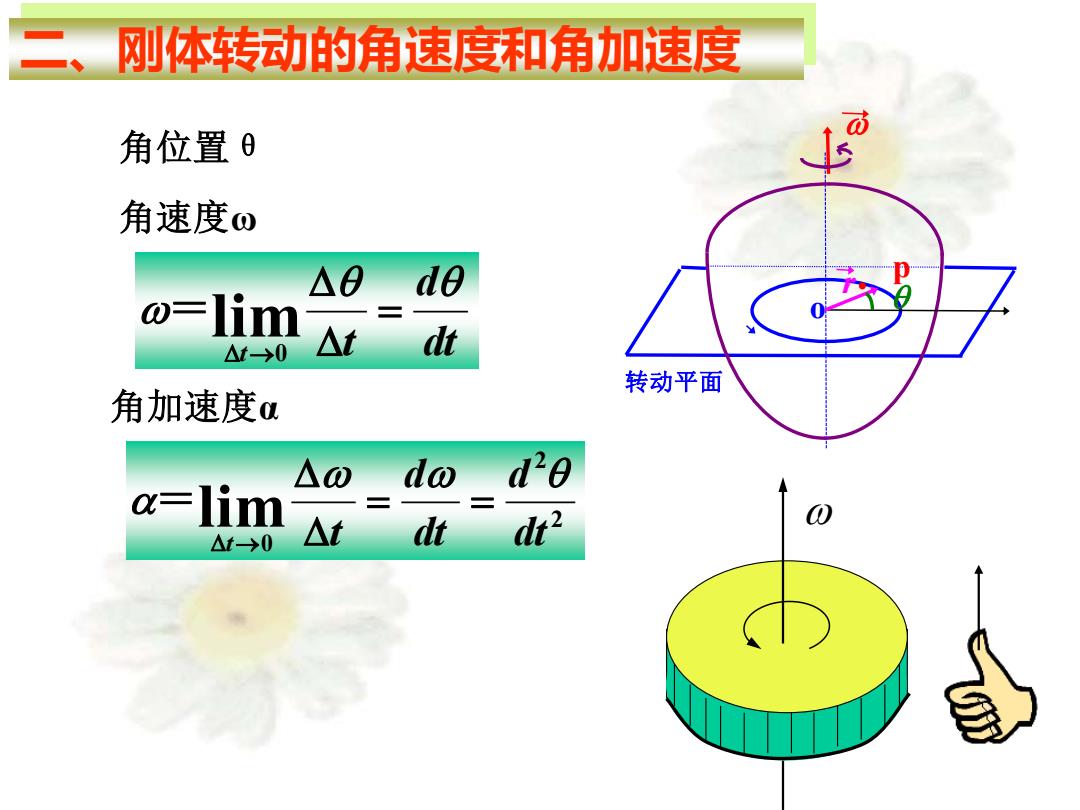
刚体转动的角速度和角加速度 角位置0 角速度o △0 de @=lim △t→0 △t dt 转动平面 角加速度α @=lim △0 do d20 △t→0 △t dt dt2
二、刚体转动的角速度和角加速度 角位置θ 角速度ω dt d t t = → lim 0 = 角加速度α 2 2 0 lim dt d dt d t t = = → = · p r o 转动平面

三、匀变速转动 当刚体定轴转动时,如果在任意相等的时间间隔内,角速度 的增量都是相等的,这种变速转动叫做匀变速转动。 角加速度 a-const 角速度 ⊙=00+0t 角位移 △0=w,t+at2 角位置 21 8+@,i+2ar 四、角量与线量的关系 速度 切向加速度 a, =ra 法向加速度 a.. =r02
三、匀变速转动 当刚体定轴转动时,如果在任意相等的时间间隔内,角速度 的增量都是相等的,这种变速转动叫做匀变速转动。 角加速度 =const 角速度 t =0 + 角位移 2 0 2 1 = t + t 角位置 2 0 0 2 1 = + t + t 四、角量与线量的关系 速度 v = r 切向加速度 at = r 2 法向加速度 an = r o P v r

例题、一转动的轮子由于摩擦力矩的作用,在5s内角速度 由15rad/s匀减速地降到10rad/s。求:(1)角加速度;(2)在此5s 内转过的圈数;(3)还需要多少时间轮子停止转动。 解根据题意,角加速度为恒量。 (1)利用公式 3) 再利用 0-w0_10-15 0= =-Irad/s 2 @o 10rad/s 5 0=0 (2)利用公式 t= 0-0,= 02-m_102-152 =62.5rad 20 2×(-1) 10s 5秒内转过的圈数 N= 0-8o 62.5 =10圈。 2元 2×3.14
例题、 一转动的轮子由于摩擦力矩的作用,在5s内角速度 由15rad/s 匀减速地降到10rad/s 。求:(1)角加速度;(2)在此5s 内转过的圈数;(3)还需要多少时间轮子停止转动。 解 根据题意,角加速度为恒量。 (1) 利用公式 2 1rad/s 5 0 10 15 = − − = = t - (2) 利用公式 62.5rad 2 ( 1) 10 15 2 2 2 2 0 2 0 = − − = − − = 5秒内转过的圈数 10圈 。 2 3.14 62.5 2 0 = = − = N (3) 再利用 10s 1 0 10 0 10rad/s 0 0 = − − = − = = = t
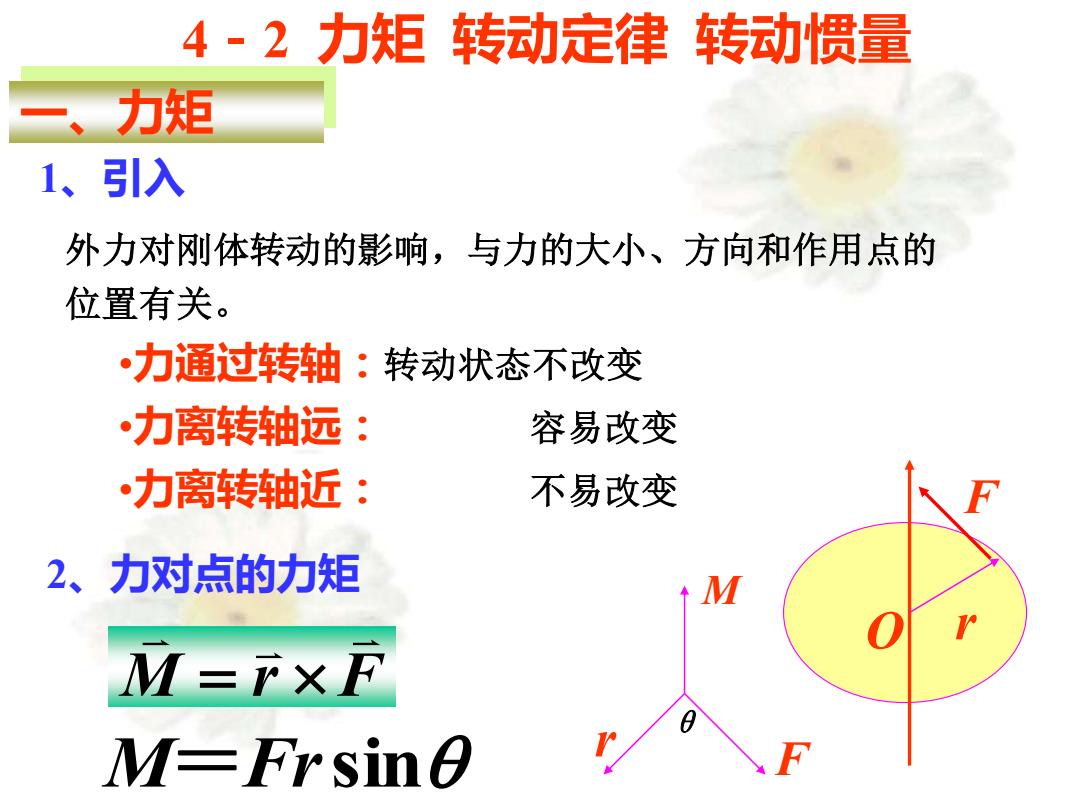
4-2力矩转动定律转动惯量 一、力矩 1、引入 外力对刚体转动的影响,与力的大小、方向和作用点的 位置有关。 •力通过转轴:转动状态不改变 力离转轴远: 容易改变 力离转轴近: 不易改变 2、力对点的力矩 M=rxF M-FrsinO
4-2 力矩 转动定律 转动惯量 一、力矩 1、引入 外力对刚体转动的影响,与力的大小、方向和作用点的 位置有关。 •力通过转轴:转动状态不改变 •力离转轴远: 容易改变 •力离转轴近: 不易改变 2、力对点的力矩 M r F = r F O M=Frsin r F M θ

3、力对转轴的力矩 力对O点的力矩在通过O点的轴上的 投影称为力对转轴的力矩 情况1:力与轴平行,则M=0 情况2:刚体所受的外力F 在垂直于转轴的平面内 力臂:转轴和力的作用线 之间的距离d称为力对转 轴的力臂。 力矩:力的大小与力臂的 乘积,称为力F对转轴的 力矩。M=Fd
3、力对转轴的力矩 •情况1:力与轴平行,则M=0 力对O点的力矩在通过O点的轴上的 投影称为力对转轴的力矩 •情况2:刚体所受的外力F 在垂直于转轴的平面内 力臂:转轴和力的作用线 之间的距离d称为力对转 轴的力臂。 力矩:力的大小与力臂的 乘积,称为力F对转轴的 力矩。M=Fd o r d F