
海大理学院煮学解件 大学物理学电子教案 热力学第一定律 6一1气体物态参量平衡态理想 气体物态方程 6一2准静态过程功热量 6一3内能热力学第一定律 6一4理想气体的等体过程和等压 过程摩尔热容
大学物理学电子教案 海大理学院教学课件 热力学第一定律 6-1 气体物态参量 平衡态 理想 气体物态方程 6-2 准静态过程 功 热量 6-3 内能 热力学第一定律 6-4 理想气体的等体过程和等压 过程 摩尔热容

第二部分热学 1.什么是热学 宏观物体是由大量的微观粒子一分子、原子等组成的 ·微观粒子的无规则的运动,称为热运动 •热学是研究热运动的规律及其对物质宏观性质的影响,以 及与其他运动形态之间的转化的物理学分支 2.热学的分类 按照研究方法的不同,热学分为 热力学 宏观理论 统计物理学 微观理论
第二部分 热学 1.什么是热学 •宏观物体是由大量的微观粒子——分子、原子等组成的 •微观粒子的无规则的运动,称为热运动 •热学是研究热运动的规律及其对物质宏观性质的影响,以 及与其他运动形态之间的转化的物理学分支 2.热学的分类 按照研究方法的不同,热学分为 热力学 ——宏观理论 统计物理学——微观理论
第六章 热力学基础 热力学是研究热现象的宏观理论— 根据实验总结出来的热 力学定律,用严密的逻辑推理的方法,研究宏观物体的热力 学性质。 热力学不涉及物质的微观结构,它的主要理论基础是热力学 的三条定律。 本章的内容是热力学第一定律和热力学第二定律
第六章 热力学基础 热力学是研究热现象的宏观理论——根据实验总结出来的热 力学定律,用严密的逻辑推理的方法,研究宏观物体的热力 学性质。 热力学不涉及物质的微观结构,它的主要理论基础是热力学 的三条定律。 本章的内容是热力学第一定律和热力学第二定律

6-1气体物态参量平衡态 理想气体物态方程 气体物态参量 1、系统与外界 热力学系统(简称系统) 在热力学中,把所要研究的对象,即由大量微观粒子 组成的物体或物体系称为热力学系统。 系统的外界(简称外界) 能够与所研究的热力学系统发生相互作用的其它物体, 称为外界
6-1 气体物态参量 平衡态 理想气体物态方程 一、气体物态参量 1、系统与外界 热力学系统(简称系统) 在热力学中,把所要研究的对象,即由大量微观粒子 组成的物体或物体系称为热力学系统。 系统的外界(简称外界) 能够与所研究的热力学系统发生相互作用的其它物体, 称为外界

2、气体的物态参量 把用来描述系统宏观状态的物理量称为状态参量。 气体的宏观状态可以用V、P、T描述 体积V一几何参量 压强即—力学参量 温度T—热力学参量 3、说明 ()气体的p、V、T是描述大量分子热运动集体特征的物理量, 是宏观量,而气体分子的质量、速度等是描述个别分子运动的 物理量,是微观量。 (2)根据系统的性质,可能还需要引入化学参量、电磁参量等
2、气体的物态参量 把用来描述系统宏观状态的物理量称为状态参量。 气体的宏观状态可以用V、P、T 描述 体积V—— 几何参量 压强p——力学参量 温度T——热力学参量 3、说明 (1)气体的p、V、T 是描述大量分子热运动集体特征的物理量, 是宏观量,而气体分子的质量、速度等是描述个别分子运动的 物理量,是微观量。 (2) 根据系统的性质,可能还需要引入化学参量、电磁参量等

,p、V、T的单位 1、气体的体积V 气体的体积V是指气体分子无规则热运动所能到达的空间。 对于密闭容器中的气体,容器的体积就是气体的体积。 单位:m的 2、压强D 压强P是大量分子与容器壁相碰撞而产生的,它等于容器 壁上单位面积所受到的正压力。p=FS 单位:1Pa=1N.m2 标准大气压1atm=76cm.Hg=1.013X105Pa 3、温度T 温度的高低反映分子热运动激③)华氏温标F,单位℉ 烈程度。 32F一水的三相点温度 (1)热力学温标T,单位:K 2120F 水的沸腾点温度 (2)摄氏温标t,单位:0C 关系: 0C一水的三相点温度 T=273.15+t 100C—水的沸腾点温度 F=9t/5+32
二、p 、V、T 的单位 1、气体的体积V 气体的体积V是指气体分子无规则热运动所能到达的空间。 对于密闭容器中的气体,容器的体积就是气体的体积。 单位:m3 2、压强p 压强P是大量分子与容器壁相碰撞而产生的,它等于容器 壁上单位面积所受到的正压力。 p=F/S 单位: 1Pa=1N.m-2 标准大气压1atm=76cm.Hg=1.013×105Pa 3、温度T 温度的高低反映分子热运动激 烈程度。 (1)热力学温标T,单位:K (2)摄氏温标t ,单位:0C 0 0C——水的三相点温度 1000C——水的沸腾点温度 (3)华氏温标F, 单位0F 320F ——水的三相点温度 2120F——水的沸腾点温度 关系: T=273.15+t F=9t/5+32
三、平衡态 1、 定义 一个系统与外界之间没有能量和物质的传递,系统的能量也 没有转化为其它形式的能量,系统的组成及其质量均不随时 间而变化,这样的状态叫做热力学平衡态。 2、说明 (1)平衡态是一个理想状态; (2)平衡态是一种动态平衡: (3)对于平衡态,可以用pV图 上的一个点来表示。 3、热力学第零定律或热平衡定律 如果两个系统分别与处于确定 热力学第零定律表明,处在同 状态的第三个系统达到热平衡, 一平衡态的所有热力学系统都 则这两个系统彼此也将处于热 有一个共同的宏观性质,这个 平衡。 决定系统热平衡的宏观性质的 物理量可以定义为温度
三、平衡态 一个系统与外界之间没有能量和物质的传递,系统的能量也 没有转化为其它形式的能量,系统的组成及其质量均不随时 间而变化,这样的状态叫做热力学平衡态。 1、定义 2、说明 (1)平衡态是一个理想状态; (2)平衡态是一种动态平衡; (3)对于平衡态,可以用pV 图 上的一个点来表示。 p V 如果两个系统分别与处于确定 状态的第三个系统达到热平衡, 则这两个系统彼此也将处于热 平衡。 3、热力学第零定律或热平衡定律 热力学第零定律表明,处在同 一平衡态的所有热力学系统都 有一个共同的宏观性质,这个 决定系统热平衡的宏观性质的 物理量可以定义为温度

四、理想气体的物态万程 1、物态方程 在、V、T三个状态参量之间一定存在某种关系,即其中一 个状态参量是其它两个状态参量的函数,如 T-TPV -一 定量气体处于平衡态时的物态方程 2、理想气体的定义 在温度不太低(与室温相比)和压强不太大(与大气压相比)时, 有三条实验定律 Boyle-Mariotte定律 等温过程中p=const Gay-Lussac定律 等体过程中 p/T=const Charles定律 等压过程中 VT=const Avogadro定律:在同样的温度和压强下,相同体积的气体含 有相同数量的分子。在标准状态下,1摩尔任何气体所占有的 体积为22.4升。 理想气体的定义:在任何情况下都遵守上述三个实验定律和 Avogadro定律的气体称为理想气体
四、理想气体的物态方程 1、物态方程 在p、V、T 三个状态参量之间一定存在某种关系,即其中一 个状态参量是其它两个状态参量的函数,如 T=T(P,V) ——一定量气体处于平衡态时的物态方程 2、理想气体的定义 在温度不太低(与室温相比)和压强不太大(与大气压相比)时, 有三条实验定律 Boyle-Mariotte定律 等温过程中 pV=const Gay-Lussac定律 等体过程中 p/T=const Charles定律 等压过程中 V/T=const Avogadro定律:在同样的温度和压强下,相同体积的气体含 有相同数量的分子。在标准状态下,1摩尔任何气体所占有的 体积为22.4升。 理想气体的定义:在任何情况下都遵守上述三个实验定律和 Avogadro定律的气体称为理想气体
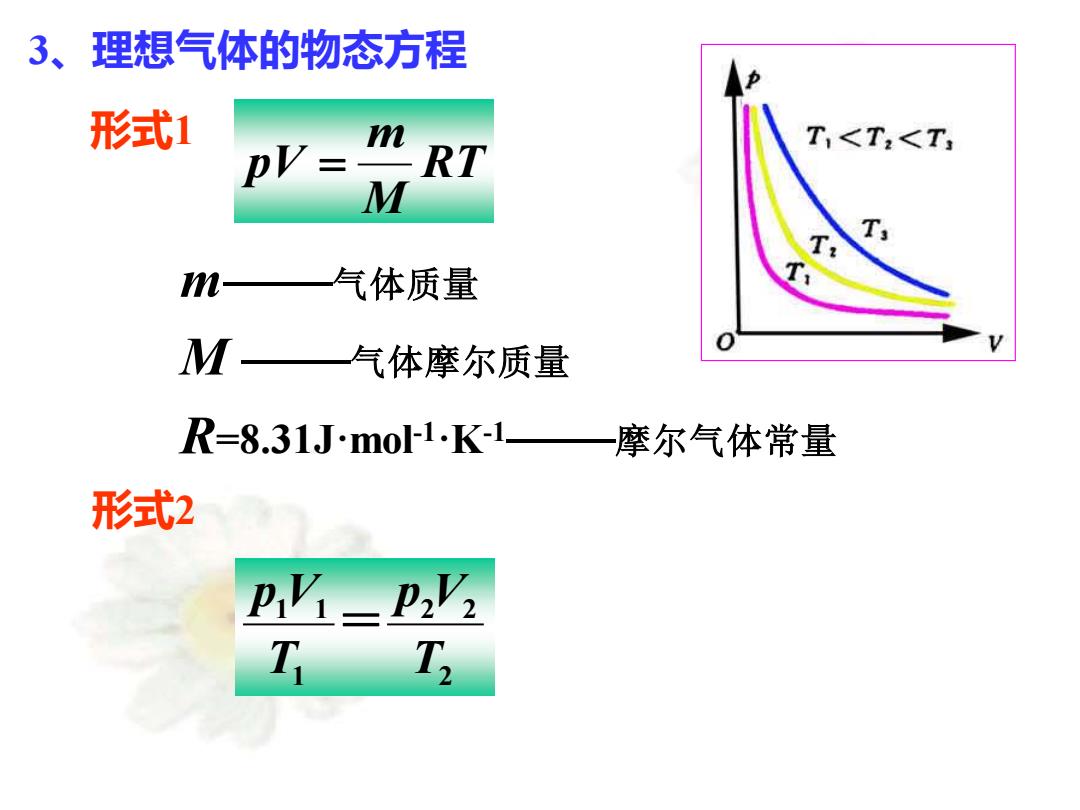
3、理想气体的物态方程 形式1 T<T:<T, DV: RT M m- 气体质量 M 气体摩尔质量 R=8.31Jmo1K1一摩尔气体常量 形式2 PV=P2V2 T T
3、理想气体的物态方程 形式1 RT M m pV = m——气体质量 M ——气体摩尔质量 R=8.31J·mol-1·K-1——摩尔气体常量 形式2 2 2 2 1 1 1 T p V T pV =

6-2准静态过程功热量 准静态过程 1、热力学过程 当系统的状态随时间变化时, 我们就说系统在经历一个热力 学过程,简称过程。 推进活塞压缩汽缸内 的气体时,气体的体 2、非静态过程 积、密度、温度或压 强都将变化 在热力学过程的发生时, 系统往往由一个平衡状 态经过一系列状态变化 为从平衡态破坏到新平 后到达另一平衡态。如 衡态建立所需的时间称 果中间状态为非平衡态, 为弛豫时间。 则此过程称非静态过 程
6-2 准静态过程 功 热量 一、准静态过程 1、热力学过程 当系统的状态随时间变化时, 我们就说系统在经历一个热力 学过程,简称过程。 推进活塞压缩汽缸内 的气体时,气体的体 积、密度、温度或压 强都将变化 2、非静态过程 在热力学过程的发生时, 系统往往由一个平衡状 态经过一系列状态变化 后到达另一平衡态。如 果中间状态为非平衡态, 则此过程称非静态过 程。 为从平衡态破坏到新平 衡态建立所需的时间称 为弛豫时间