
海大理学院栽学裸件 大学物理学电子教案 电流、欧姆定律和电动势 10-5基尔霍夫定律 10-6电容器的充放电
大学物理学电子教案 海大理学院教学课件 电流、欧姆定律和电动势 10-5 基尔霍夫定律 10-6 电容器的充放电

复习 电流电流密度 。 电阻率欧姆定律的微分形式 电源电动势 全电路欧姆定律
复 习 • 电流 电流密度 • 电阻率 欧姆定律的微分形式 • 电源 电动势 • 全电路欧姆定律

10-5 基尔霍夫定律 引言: 用欧姆定律只能处理一些简单电路的问题。而许多实际问题, 其电阻的联接既不是并联,又不是串联,不能用欧姆定律进行 计算。为了进行这类电路的运算,人们总结出了一些有效的方 法,如等效发电机原理、叠加原理、三角形与星形变换原理等。 本节我们介绍基尔霍夫定律,它包括两条定律。 基尔霍夫Gustav Robert Kirchhoff,1824-1887) 德国物理学家。他对物理学的贡献颇多。 1845年提出电路的基尔霍夫定律,1859年与 本生创立了光谱分析法;同年,在太阳吸收 光谱线的研究中,他得出了热辐射的基尔霍 夫定律,于1862年提出了绝对黑体的概念, 这两者乃是开辟20世纪物理学新纪元的关键 之一
10-5 基尔霍夫定律 引言: 用欧姆定律只能处理一些简单电路的问题。而许多实际问题, 其电阻的联接既不是并联,又不是串联,不能用欧姆定律进行 计算。为了进行这类电路的运算,人们总结出了一些有效的方 法,如等效发电机原理、叠加原理、三角形与星形变换原理等。 本节我们介绍基尔霍夫定律,它包括两条定律。 基尔霍夫Gustav Robert Kirchhoff,1824-1887) 德国物理学家。他对物理学的贡献颇多。 1845年提出电路的基尔霍夫定律,1859年与 本生创立了光谱分析法;同年,在太阳吸收 光谱线的研究中,他得出了热辐射的基尔霍 夫定律,于1862年提出了绝对黑体的概念, 这两者乃是开辟20世纪物理学新纪元的关键 之一
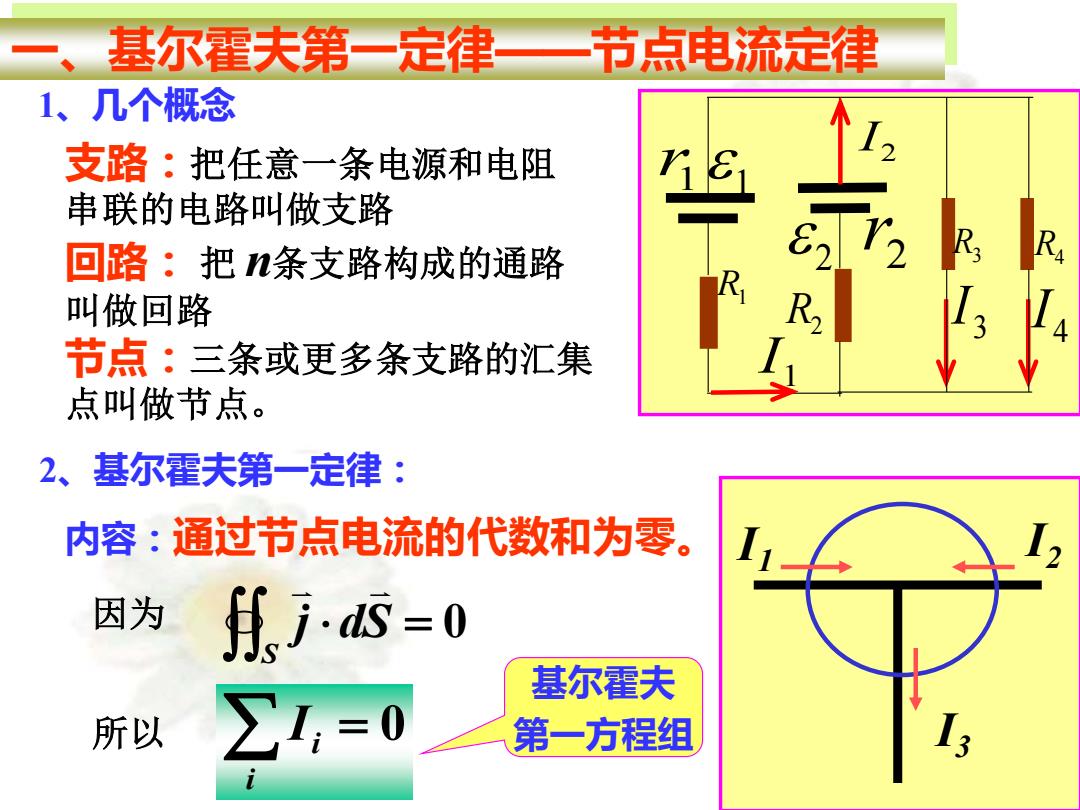
一、基尔霍夫第一定律 节点电流定律 1、几个概念 支路:把任意一条电源和电阻 串联的电路叫做支路 回路:把n条支路构成的通路 叫做回路 节点:三条或更多条支路的汇集 点叫做节点。 2、基尔霍夫第一定律: 内容:通过节点电流的代数和为零。 因为 fj.=0 基尔霍夫 所以 ∑1=( 第一方程组
= 0 S j dS = 0 i i I 因为 内容:通过节点电流的代数和为零。 2、基尔霍夫第一定律: 一、基尔霍夫第一定律——节点电流定律 支路:把任意一条电源和电阻 串联的电路叫做支路 回路: 把 n条支路构成的通路 叫做回路 节点:三条或更多条支路的汇集 点叫做节点。 2 R1 2 r 1 R2 1 r 4 I R4 2 I 1 I 3 I R3 1、几个概念 所以 基尔霍夫 第一方程组 I I1 2 I3
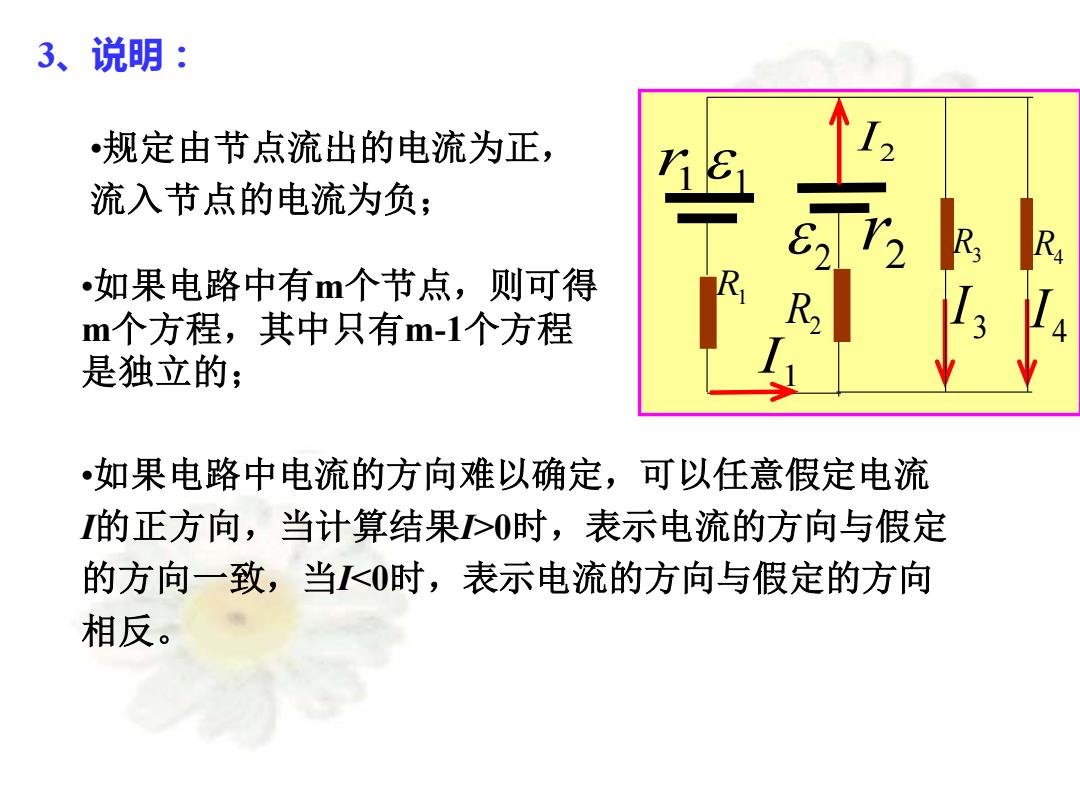
3、说明: 规定由节点流出的电流为正, 流入节点的电流为负 2T2 如果电路中有m个节点,则可得 R m个方程,其中只有m-1个方程 R 是独立的; •如果电路中电流的方向难以确定,可以任意假定电流 的正方向,当计算结果>0时,表示电流的方向与假定 的方向一致,当<0时,表示电流的方向与假定的方向 相反
2 R1 2 r 1 R2 1 r 4 I R4 2 I 1 I 3 I R3 3、说明: •规定由节点流出的电流为正, 流入节点的电流为负; •如果电路中有m个节点,则可得 m个方程,其中只有m-1个方程 是独立的; •如果电路中电流的方向难以确定,可以任意假定电流 I的正方向,当计算结果I>0时,表示电流的方向与假定 的方向一致,当I<0时,表示电流的方向与假定的方向 相反
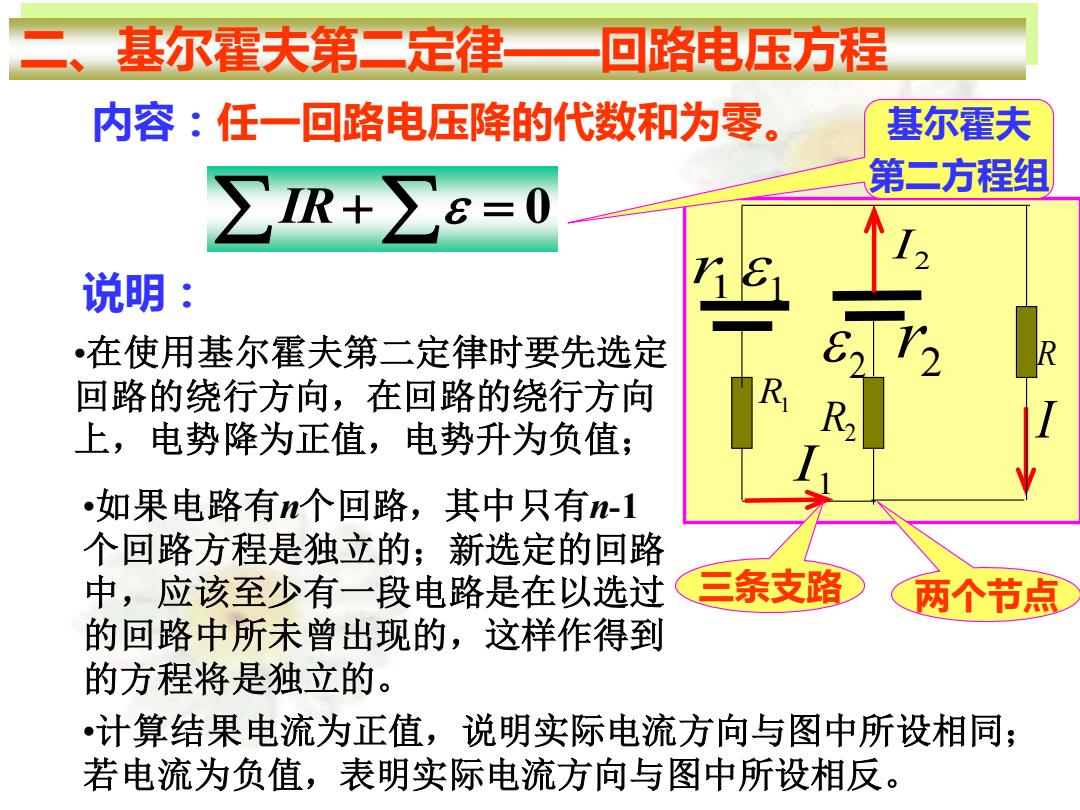
二、 基尔霍夫第二定律 回路电压方程 内容:任一回路电压降的代数和为零。 基尔霍夫 ∑IR+∑=0 第二方程组 说明: •在使用基尔霍夫第二定律时要先选定 回路的绕行方向,在回路的绕行方向 上,电势降为正值,电势升为负值; R 如果电路有n个回路,其中只有m-1 个回路方程是独立的;新选定的回路 中,应该至少有一段电路是在以选过 三条支路 两个节点 的回路中所未曾出现的,这样作得到 的方程将是独立的。 •计算结果电流为正值,说明实际电流方向与图中所设相同; 若电流为负值,表明实际电流方向与图中所设相反
二、基尔霍夫第二定律——回路电压方程 •在使用基尔霍夫第二定律时要先选定 回路的绕行方向,在回路的绕行方向 上,电势降为正值,电势升为负值; 2 R1 2 r I 1 R2 1 r R 2 I 1 I 三条支路 两个节点 内容:任一回路电压降的代数和为零。 IR+ = 0 基尔霍夫 第二方程组 说明: •如果电路有n个回路,其中只有n-1 个回路方程是独立的;新选定的回路 中,应该至少有一段电路是在以选过 的回路中所未曾出现的,这样作得到 的方程将是独立的。 •计算结果电流为正值,说明实际电流方向与图中所设相同; 若电流为负值,表明实际电流方向与图中所设相反
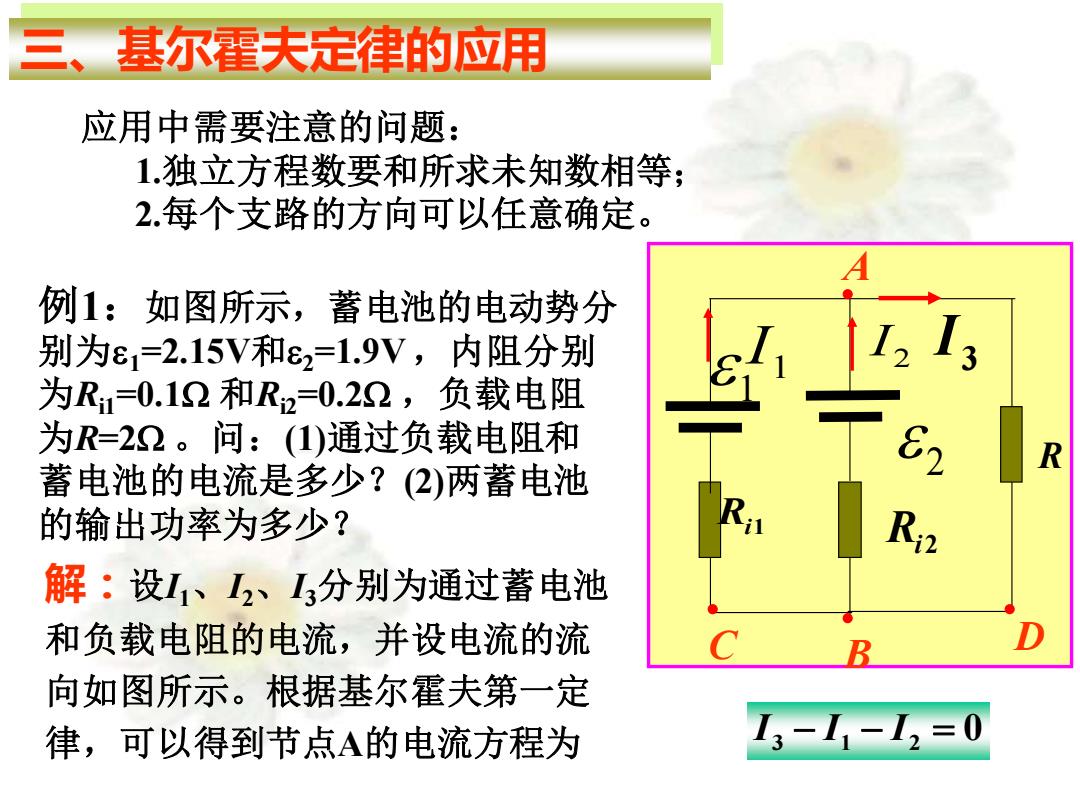
三、基尔霍夫定律的应用 应用中需要注意的问题: 1.独立方程数要和所求未知数相等; 2.每个支路的方向可以任意确定。 例1:如图所示,蓄电池的电动势分 别为e1=2.15V和82=1.9V,内阻分别 为R1=0.12和R2=0.22,负载电阻 为R=2Ω。问:(1)通过负载电阻和 蓄电池的电流是多少?(2)两蓄电池 的输出功率为多少? 解:设L1、2、13分别为通过蓄电池 和负载电阻的电流,并设电流的流 向如图所示。根据基尔霍夫第一定 律,可以得到节点A的电流方程为 3-1-L2=0
三、基尔霍夫定律的应用 应用中需要注意的问题: 1.独立方程数要和所求未知数相等; 2.每个支路的方向可以任意确定。 例 1 :如图所示,蓄电池的电动势分 别为 1=2.15V 和 2=1.9V ,内阻分别 为 Ri1=0.1 W 和 Ri2=0.2 W ,负载电阻 为 R=2 W 。问:(1)通过负载电阻和 蓄电池的电流是多少?(2)两蓄电池 的输出功率为多少? 2 Ri1 3 I 1 Ri 2 R 2 I 1I A C B D 解: 设 I1 、 I2 、 I3分别为通过蓄电池 和负载电阻的电流,并设电流的流 向如图所示。根据基尔霍夫第一定 律,可以得到节点 A的电流方程为 I3 − I1 − I2 = 0
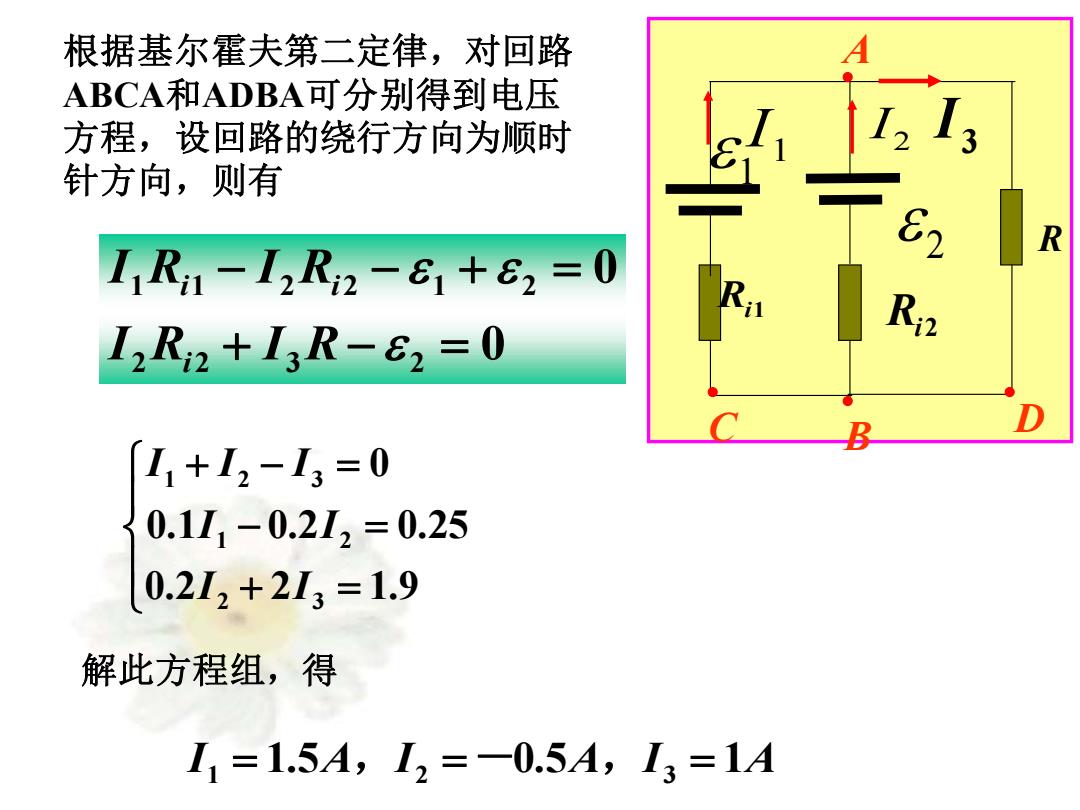
根据基尔霍夫第二定律,对回路 ABCA和ADBA可分别得到电压 方程,设回路的绕行方向为顺时 针方向,则有 I1R1-I2R2-61+62=0 I2R2+I3R-62=0 D I1+12-13=0 0.111-0.2I2=0.25 0.212+2L3=1.9 解此方程组,得 I1=1.5A,I2=-0.5A,I3=1A
2 Ri1 3 I 1 Ri 2 R 2 I 1 I A C B D 根据基尔霍夫第二定律,对回路 ABCA和ADBA可分别得到电压 方程,设回路的绕行方向为顺时 针方向,则有 0 0 2 2 3 2 1 1 2 2 1 2 + − = − − + = I R I R I R I R i i i + = − = + − = 0.2 2 1.9 0.1 0.2 0.25 0 2 3 1 2 1 2 3 I I I I I I I 解此方程组,得 I1 = 1.5A,I2 =-0.5A,I3 = 1A

负载电阻R两端的电势降为 U=I3R=1×2=2V 蓄电池1的输出功率为 P=IU=1.5×2=3W 蓄电池2的输出功率为 P,=I,U=-0.5×2=-1W 消耗在负载电阻上的功率为 P=IR=12×2=2W 讨论:蓄电池不仅没有输出功率,相反从外部获得了功率, 处于被充电状态。由此可知,电动势值不同的几个蓄电池并 联后供给负载的电流,并不一定比一个蓄电池大,有时电动 势较小的蓄电池却变成了电路中的负载,在使用时应该尽量 避免这种情况出现
负载电阻R两端的电势降为 U = I3 R = 12 = 2V 蓄电池1的输出功率为 P1 = I1 U = 1.52 = 3W P2 = I2 U = −0.52 = −1W 蓄电池2的输出功率为 消耗在负载电阻上的功率为 P3 =I3 2 R=1 2 2=2W 讨论:蓄电池不仅没有输出功率,相反从外部获得了功率, 处于被充电状态。由此可知,电动势值不同的几个蓄电池并 联后供给负载的电流,并不一定比一个蓄电池大,有时电动 势较小的蓄电池却变成了电路中的负载,在使用时应该尽量 避免这种情况出现
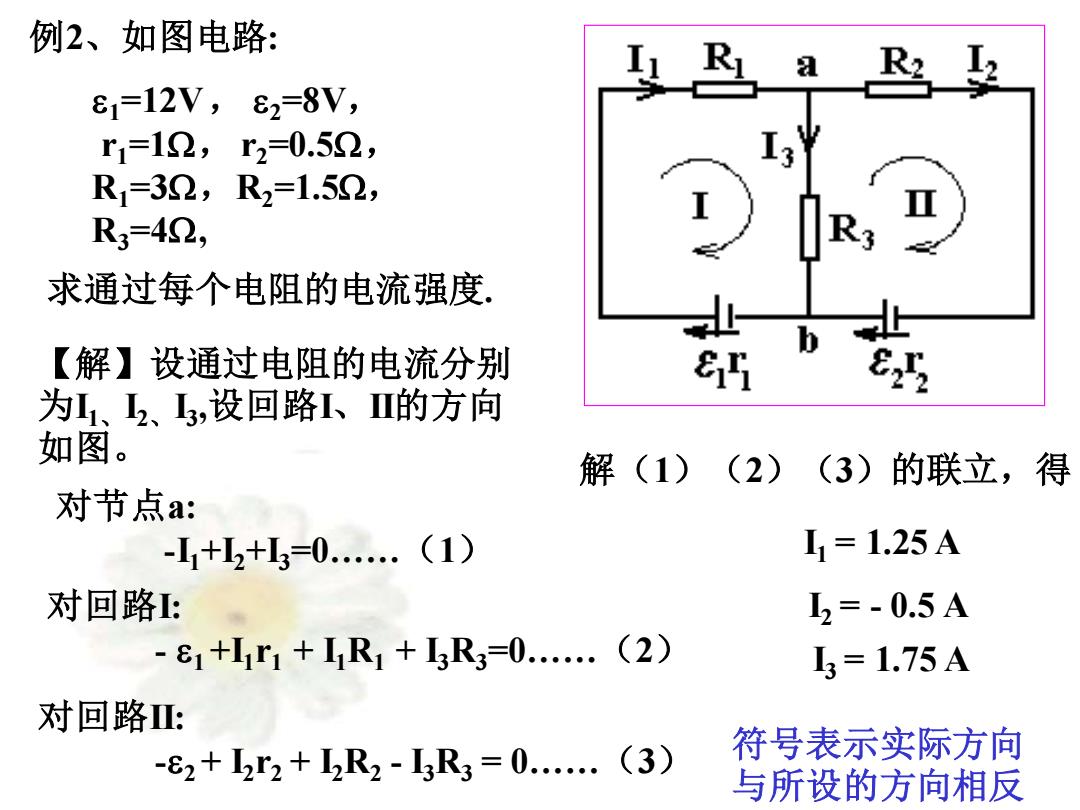
例2、如图电路: a 81=12V,82=8V, r1=12,r2=0.52, R1=32,R2=1.52, R3=42, 求通过每个电阻的电流强度! 【解】设通过电阻的电流分别 为1、2、3,设回路1、Ⅲ的方向 如图。 解(1) (2) (3)的联立,得 对节点a: -1+2+3=0..(1) 11=1.25A 对回路 2=-0.5A 81+I1r1+I1R1+3R3=0..(2) - 3=1.75A 对回路: -82+2r2+2R2-3R3=0.…(3) 符号表示实际方向 与所设的方向相反
例2、如图电路: 1=12V, 2=8V, r1=1W, r2=0.5W, R1=3W,R2=1.5W, R3=4W, 求通过每个电阻的电流强度. 【解】设通过电阻的电流分别 为I1、I2、I3 ,设回路I、II的方向 如图。 对节点a: -I1+I2+I3=0……(1) 对回路I: - 1 +I1r1 + I1R1 + I3R3=0……(2) 对回路II: -2 + I2r2 + I2R2 - I3R3 = 0……(3) 解(1)(2)(3)的联立,得 I1 = 1.25 A I2 = - 0.5 A 符号表示实际方向 与所设的方向相反 I3 = 1.75 A