
一海大理学院表号髁件 大学物理学电子教案 电磁感应— 磁场的能量 电磁场基本方程
大学物理学电子教案 海大理学院教学课件 电磁感应——磁场的能量 电磁场基本方程

复习 ·感生电动势 f.=-儿西 ·自感 Φ=LI 8,=-L dt ·互感 Φ21=MM1④12=M 821= dΦ21=-M dt dt dΦ2 =-M dt dt
复 习 • 感生电动势 dS t B E dl L S k = − • 互感 dt dI i = −L • 自感 F=LI F21 = MI 1 F12 = MI 2 dt dI M dt d 21 1 21 = − F =- dt dI M dt d 12 2 12 = − F =-
13-5磁场的能量 引入: 电容器充电,储存电场能量 w.-1qv-1cu 电场能量密度 w20000000 1 。=。E2 电流激发磁场,也要供给能量,所以磁场具有能量。 当线圈中通有电流时,在其周围建立了磁场,所储存的磁能 等于建立磁场过程中,电源反抗自感电动势所做的功
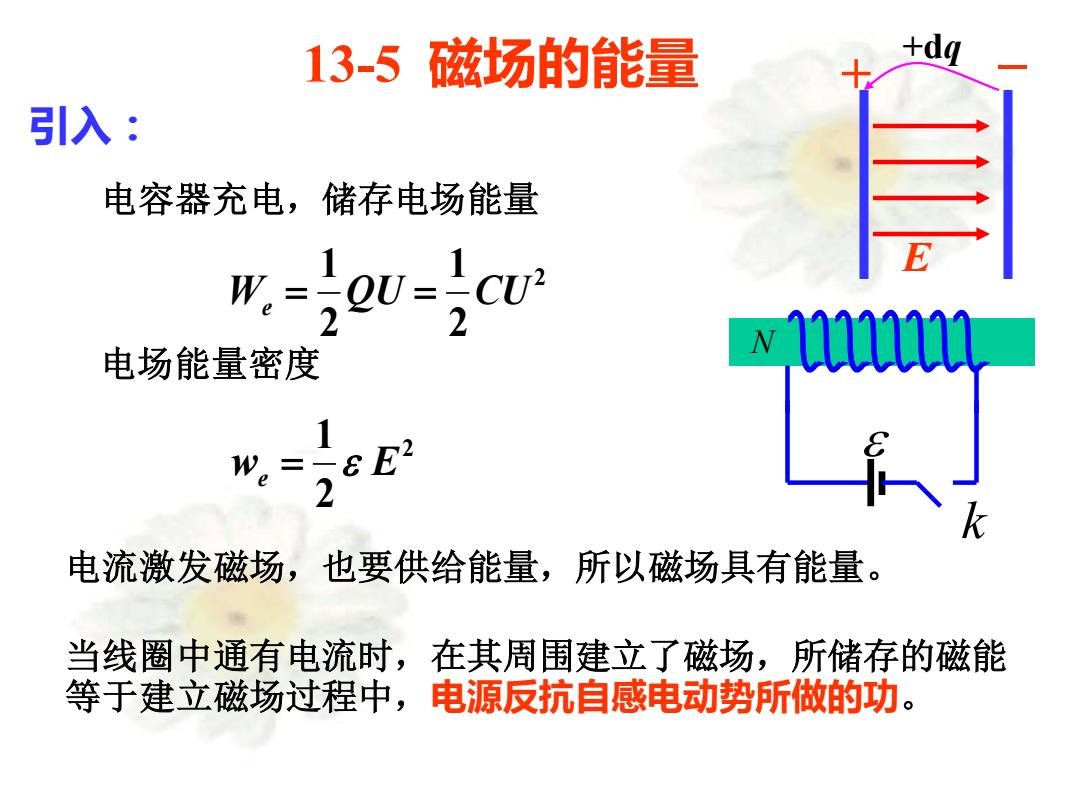
13-5 磁场的能量 引入: 电容器充电,储存电场能量 2 2 1 2 1 We = QU = CU 电流激发磁场,也要供给能量,所以磁场具有能量。 当线圈中通有电流时,在其周围建立了磁场,所储存的磁能 等于建立磁场过程中,电源反抗自感电动势所做的功。 N k 电场能量密度 2 2 1 we = E E +dq + _
线圈贮存的能量 自感磁能: 对于如图所示的电路 ε-L =RI d dt aldt LIdI RI'dt ∫sdt=∫LIdl+∫Rr2M 焦耳热 电源供给 磁场 的能量 的能量 自感线圈贮存的磁场 W.= LIdl=-LI 0
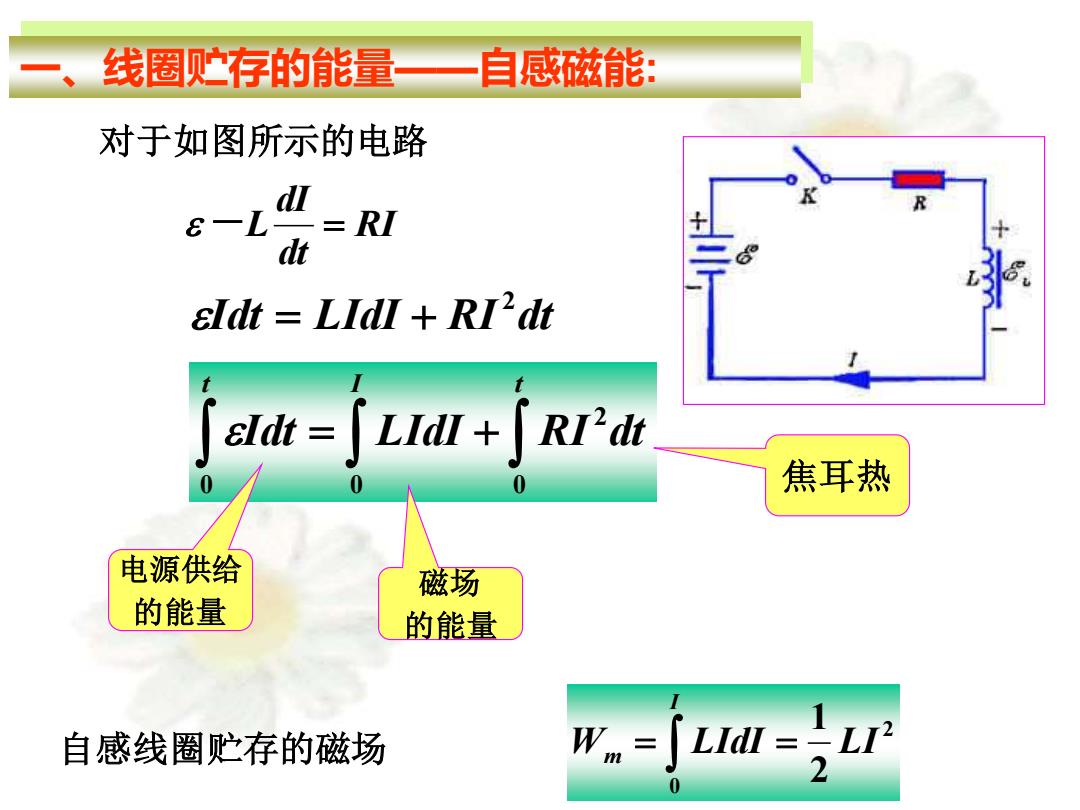
一、线圈贮存的能量——自感磁能: 对于如图所示的电路 RI dt dI -L = Idt LIdI RI dt 2 = + = + t I t Idt LIdI RI dt 0 2 0 0 电源供给 的能量 磁场 的能量 焦耳热 自感线圈贮存的磁场 2 0 2 1 W LIdI LI I m = =

二、 磁场的能量 以长直螺线管为例:当流有电流时 B=unl I=- B un L=un'y 长直螺线管的磁场能量:, 对于一般情况: 定义磁场的能量密度: B2 =-8. Wm Wm 2 24 磁场所储存的总能量: 磁场所储存的总能量: Wm = 2 dy 积分遍及磁场存在的全空间
二、磁场的能量 以长直螺线管为例:当流有电流I时 长直螺线管的磁场能量: 定义磁场的能量密度: 2 2 B wm = 磁场所储存的总能量: = = dV B Wm wm dV 2 2 B = nI n B I = L n V 2 = V B n B Wm LI n V 2 2 1 2 1 2 2 2 2 = = = 磁场所储存的总能量: = V m dV H B W 2 对于一般情况: 积分遍及磁场存在的全空间。 wm B H = 2 1

例题.同轴电缆的磁能与自感(P228) 同轴电缆中金属 芯线的半径为R, 金属圆筒半径为 2R1 R2,中间充满磁 导中为μ的磁介质, 若芯线与圆筒分 别与电池两极相 解:由题意知 连,芯线与圆筒 W 2 上的电流大小相 0 rR 2n R 同轴芯线与圆筒 1 、H2= Al2 m 之间单位长度上 82r2 的磁能与自感系 数。 2 W.- 2.1dh= 以2 -In 4元 R
例题.同轴电缆的磁能与自感(P228) 同轴电缆中金属 芯线的半径为R1, 金属圆筒半径为 R2,中间充满磁 导中为的磁介质, 若芯线与圆筒分 别与电池两极相 连,芯线与圆筒 上的电流大小相 等,方向相反, 如略去金属芯线 内的磁场,求此 同轴芯线与圆筒 之间单位长度上 的磁能与自感系 数。 解:由题意知 2 1 2 1 0 2 0 r R R r R r I r R H = 2 2 2 2 2 8 1 r I wm H = = 1 2 2 2 2 2 ln 4 2 1 8 2 1 R I R r dr r I W R R m = = 1 2 ln 2 R R L = 2 2 1 W LI m =
三、互感磁能 先使线圈1电流从0到I1,电源1 做功,储存为线圈1的自感磁能 合上开关k,电流i2增大时, 在回路1中的互感电动势: u=-Mv dt 线圈1的电源维持I,反抗互感电动势的功, 转化为磁场的能量 2=∫e41t=Mzl2=M4l2 线圈2的电流从0到I2,电源2做功 储存为线圈2的自感磁能
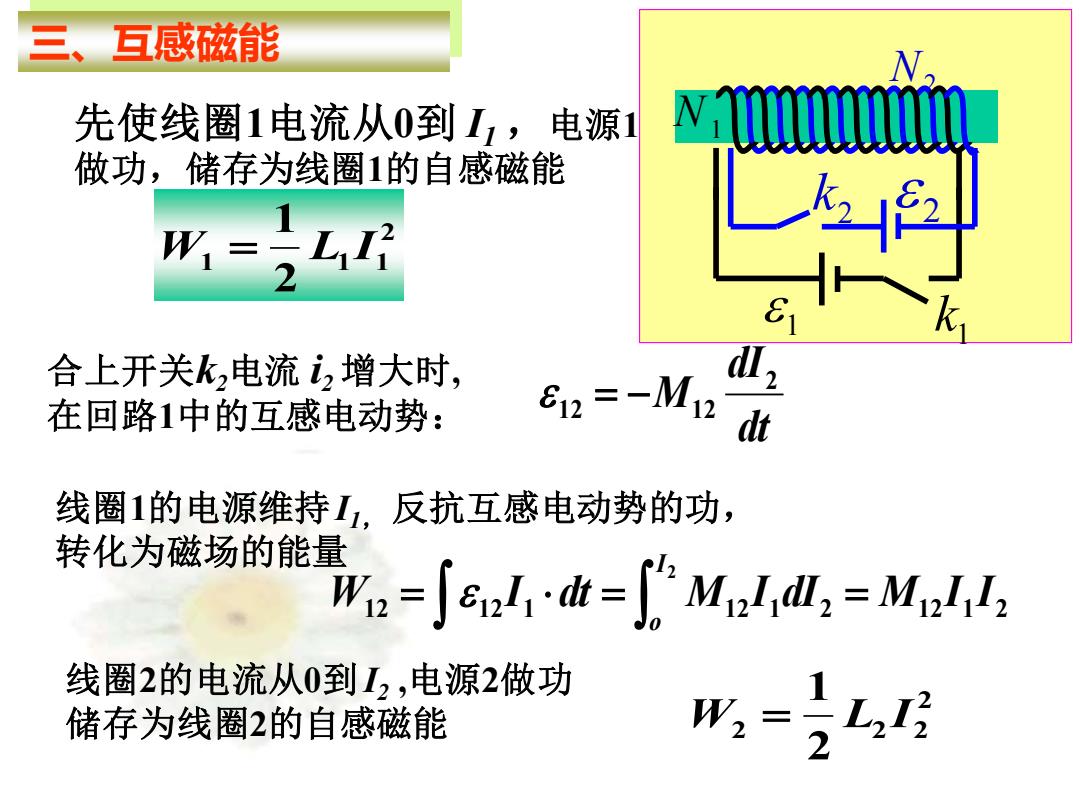
三、互感磁能 12 12 1 12 1 2 12 1 2 2 W I dt M I dI M I I I o = = = 线圈1的电源维持I1, 反抗互感电动势的功, 转化为磁场的能量 先使线圈1电流从0到 I1 ,电源1 做功,储存为线圈1的自感磁能 N2 1 2 N1 1 k 2 k dt dI M 2 12 = − 12 合上开关k2电流 i2 增大时, 在回路1中的互感电动势: 2 1 1 1 2 1 W = L I 线圈2的电流从0到I2 ,电源2做功 储存为线圈2的自感磁能 2 2 2 2 2 1 W = L I

经过上述步骤电流分别为L,和I的状态, 储存在磁场中的总磁能: 。=++=4++ 同理,先合开关k,使线圈2充电至I2,然后再合 开关k保持I,不变,给线圈1充电,得到储存在 磁场中的总能量为: W=形+g+=,1+5+M,以, 这两种通电方式的最后状态相同,所以 Wn=Wn .M2=M21=M 称MⅢ,I2为互感磁能 M为互感系数
1 2 1 2 2 2 2 2 1 2 1 2 1 1 2 1 2 1 W W W W L I L I M I I m = + + = + + 经过上述步骤电流分别为I1 和I2的状态, 储存在磁场中的总磁能: 称MI1 I2 为互感磁能 M为互感系数 2 1 2 1 2 1 1 2 2 1 2 1 2 2 2 1 2 1 W ' W W W L I L I M I I m = + + = + + M12 = M21 = M 这两种通电方式的最后状态相同,所以 ' Wm = Wm 同理,先合开关k2使线圈 2充电至 I2 ,然后再合 开关k1保持I2 不变,给线圈1 充电,得到储存在 磁场中的总能量为:

13-6位移电流、电磁场基本方程的积分形式 麦克斯韦(James Clerk Maxwell1831一1879) 他提出了有旋电场和位移电流概 念,建立了经典电磁理论,并预 言了以光速传播的电磁波的存在。 他的《电磁学通论》与牛顿时代 的《自然哲学的数学原理》并驾 19世纪伟大的英 齐驱,它是人类探索电磁规律的 国物理学家、数 一个里程碑。 学家。经典电磁 理论的奠基人, •在气体动理论方面,他还提出气 气体动理论的创 体分子按速率分布的统计规律。 始人之一
麦克斯韦(James Clerk Maxwell 1831——1879) 19世纪伟大的英 国物理学家、数 学家。经典电磁 理论的奠基人, 气体动理论的创 始人之一。 •他提出了有旋电场和位移电流概 念,建立了经典电磁理论,并预 言了以光速传播的电磁波的存在。 他的《电磁学通论》与牛顿时代 的《自然哲学的数学原理》并驾 齐驱,它是人类探索电磁规律的 一个里程碑。 •在气体动理论方面,他还提出气 体分子按速率分布的统计规律。 13-6 位移电流、电磁场基本方程的积分形式

位移电流全电流安培环路定理 1、问题的提出 在稳恒电流的磁场中,安培环路定理为 f五=1=八、j 对于曲面S1 fn.d-1 对于曲面S2 ∫H.a=0 对于非稳恒电路,传导电流不连续, 安培环路定理不成立
一、位移电流 全电流安培环路定理 1、问题的提出 在稳恒电流的磁场中,安培环路定理为 = = l S H dl I j dS 对于非稳恒电路,传导电流不连续, 安培环路定理不成立。 对于曲面S1 H dl I l = 对于曲面S2 = 0 l H dl R I0 l I0 S2 S1 I0 A B s l