
海大理学院教学裸件 大学物理学电子教案 电磁振荡与电磁波
大学物理学电子教案 海大理学院教学课件 电磁振荡与电磁波

第十六章 电磁振荡与电磁波 麦克斯韦:电磁场理论,证明电磁场以波的形式传播,波速为 光速。 赫兹:1888年用实验证明了电磁波的存在。 波波夫:1895年发明了无线电报接收机,1896年3月表演了距 离为250m的无线电报传送。 •马可尼:1897年第一次实现了9英里的无线电联系;1899年实 现了横跨英吉利海峡的无线电通讯;1901年完成了从法国穿越 大西洋到达加拿大的无线电通讯。1909年他获得了诺贝尔物理 学奖金。 内容:电磁振荡和电磁波的产生,电磁波的特性等
第十六章 电磁振荡与电磁波 •麦克斯韦:电磁场理论,证明电磁场以波的形式传播,波速为 光速。 •赫兹:1888年用实验证明了电磁波的存在。 •波波夫:1895年发明了无线电报接收机,1896年3月表演了距 离为250m的无线电报传送。 •马可尼:1897年第一次实现了9英里的无线电联系;1899年实 现了横跨英吉利海峡的无线电通讯;1901年完成了从法国穿越 大西洋到达加拿大的无线电通讯。1909年他获得了诺贝尔物理 学奖金。 内容:电磁振荡和电磁波的产生,电磁波的特性等

赫兹(Hertz.,H.R.,1857-1894) 德国物理学家 用实验证实了电磁波的存在,并确认了电磁 波是横波,具有与光类似的特性,并且实验 了两列电磁波的干涉,同时证实了在直线传 播时,电磁波的传播速度与光速相同,从而 验证了麦克斯韦的电磁理论的正确性。 1888年,成了近代科学史上的一座里程碑。 赫兹的发现具有划时代的意义,它不仅证实 了麦克斯韦发现的真理,更重要的是开创了 无线电电子技术的新纪元。 为了纪念他的功绩,人们用他的名字来命名 各种波动频率的单位,简称“赫
赫兹(Hertz, H. R. ,1857-1894) 德国物理学家 用实验证实了电磁波的存在,并确认了电磁 波是横波,具有与光类似的特性,并且实验 了两列电磁波的干涉,同时证实了在直线传 播时,电磁波的传播速度与光速相同,从而 验证了麦克斯韦的电磁理论的正确性。 1888年,成了近代科学史上的一座里程碑。 赫兹的发现具有划时代的意义,它不仅证实 了麦克斯韦发现的真理,更重要的是开创了 无线电电子技术的新纪元。 为了纪念他的功绩,人们用他的名字来命名 各种波动频率的单位,简称“赫
16-1电滋振荡 振荡电路 无阻尼自由电磁振荡 1、LC振荡电路 充电: 电容器C两极板间的电压:U。=ε 两极板上等量异号电荷:+2o、-Q0: 放电: 电路无电流,电场能量集中在 电容器两极板间
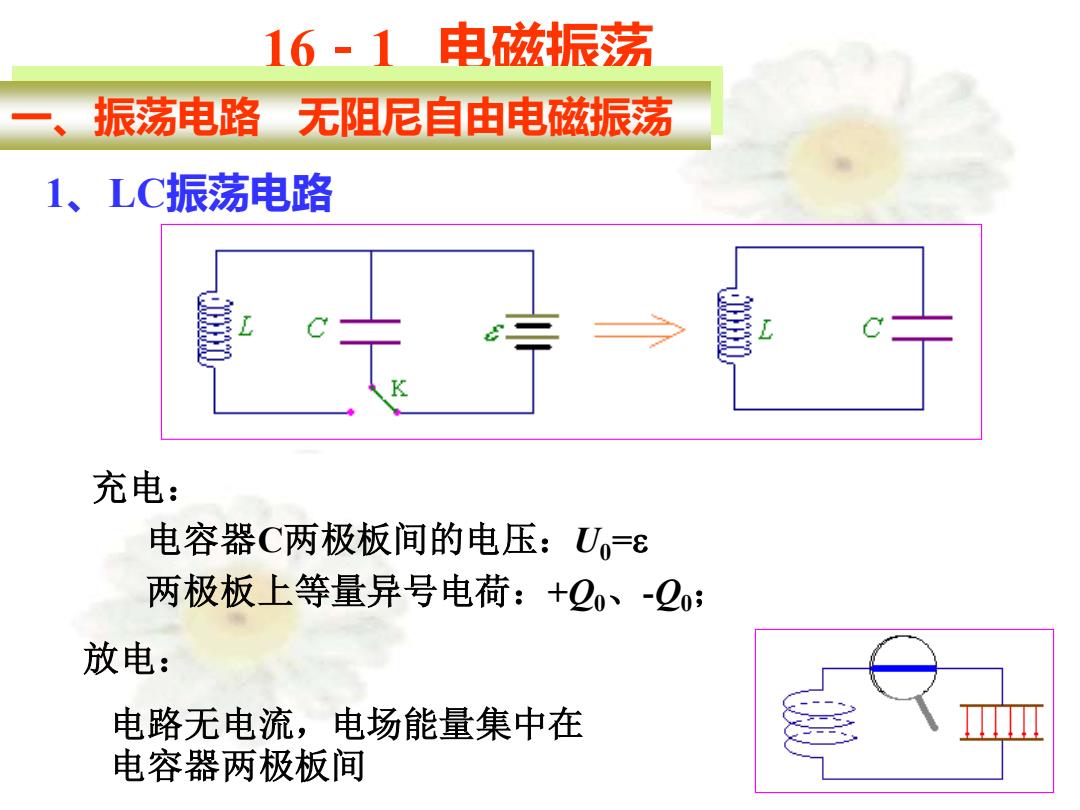
16-1 电磁振荡 一、振荡电路 无阻尼自由电磁振荡 1、LC振荡电路 充电: 电容器C两极板间的电压:U0=e 两极板上等量异号电荷:+Q0、-Q0; 放电: 电路无电流,电场能量集中在 电容器两极板间
线圈激起磁场,电路中电流逐渐增大,电 荷减小,放电终了,电容器电场能量全部 转化为磁场能量 对电容器反向充电,随着电流的减弱, 两极板上电荷逐渐增多,磁场能量又全 部转化为电场能量 电客器放电,电场能量又转化为磁场能量 演示1 演示2
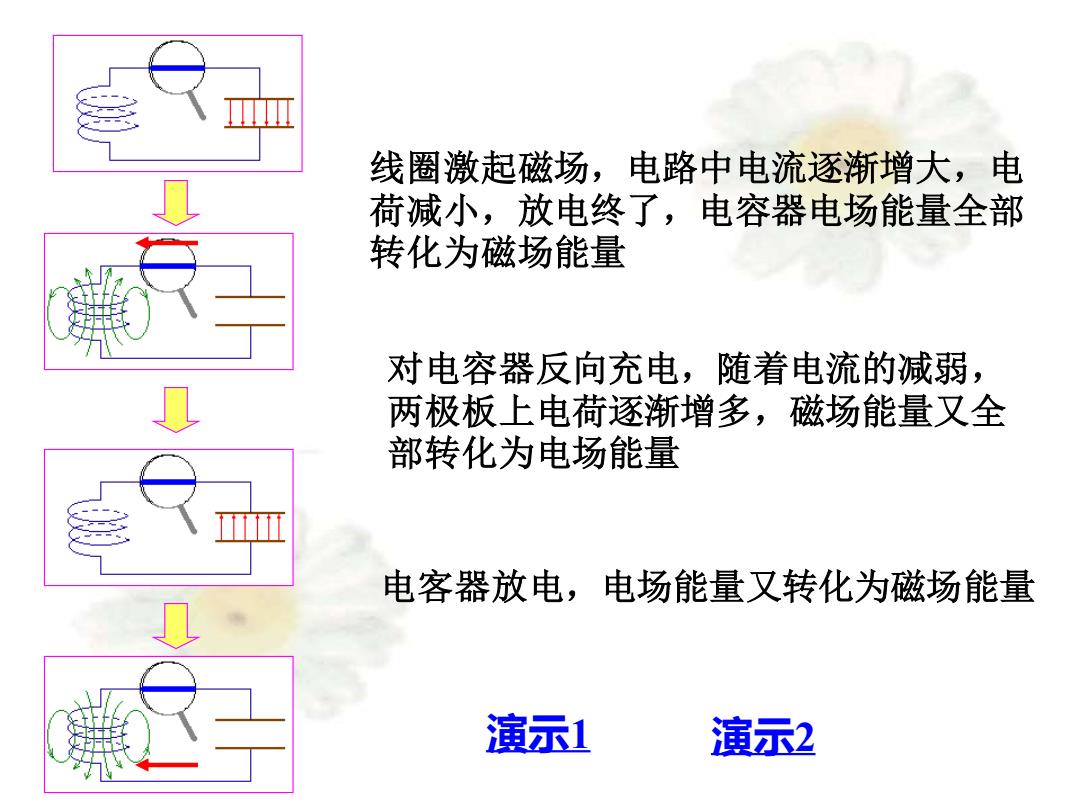
线圈激起磁场,电路中电流逐渐增大,电 荷减小,放电终了,电容器电场能量全部 转化为磁场能量 对电容器反向充电,随着电流的减弱, 两极板上电荷逐渐增多,磁场能量又全 部转化为电场能量 电客器放电,电场能量又转化为磁场能量 演示1 演示2

2、几个基本概念 电磁振荡: 电荷和电流、电场和磁场随时间作周期性变化的现象。 振荡电路: 产生电磁振荡的电路。 无阻尼自由振荡电路: 电路中没有任何能量耗散(转换为焦耳热、电磁辐射等), 称为无阻尼自由振荡电路。 振荡方程: 振荡电路所遵循的欧姆定律
2、几个基本概念 电磁振荡: 电荷和电流、电场和磁场随时间作周期性变化的现象。 振荡电路: 产生电磁振荡的电路。 无阻尼自由振荡电路: 电路中没有任何能量耗散(转换为焦耳热、电磁辐射等), 称为无阻尼自由振荡电路。 振荡方程: 振荡电路所遵循的欧姆定律
二、无阻尼电磁振荡的振荡方程 1、电量 设某时刻电路中电流为,则自感电动势 di q i= dq dt dq dt2 q=Qcos(@t+p) LC V 2m2π√LC dq+o'q-0 T==2r√LC
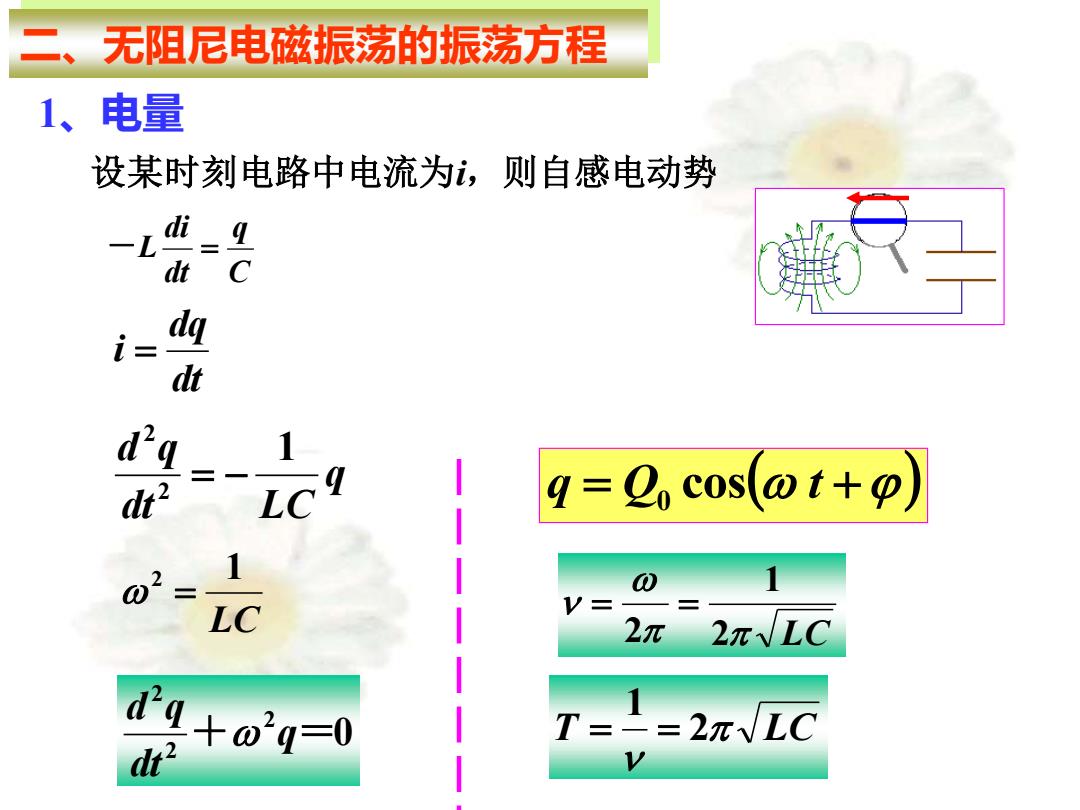
二、无阻尼电磁振荡的振荡方程 1、电量 设某时刻电路中电流为i,则自感电动势 C q dt di -L = dt dq i = q dt LC d q 1 2 2 = − LC 2 1 = 0 2 2 2 + q= dt d q q = Q cos( t +) 0 LC 2 1 2 = = T LC 2 1 = =
2、电流 把电量对时间求导 i-M--0Q,sinl@t+o) dt L0=020 --Isin+p)-lco 3、说 •电量与电流都作周期性变 化,电流相位比电量的相 位超前 LC振荡电路的频率是由振荡电路 本身的性质决定的 ·改变电感L或电容C就可以得到所 需的频率
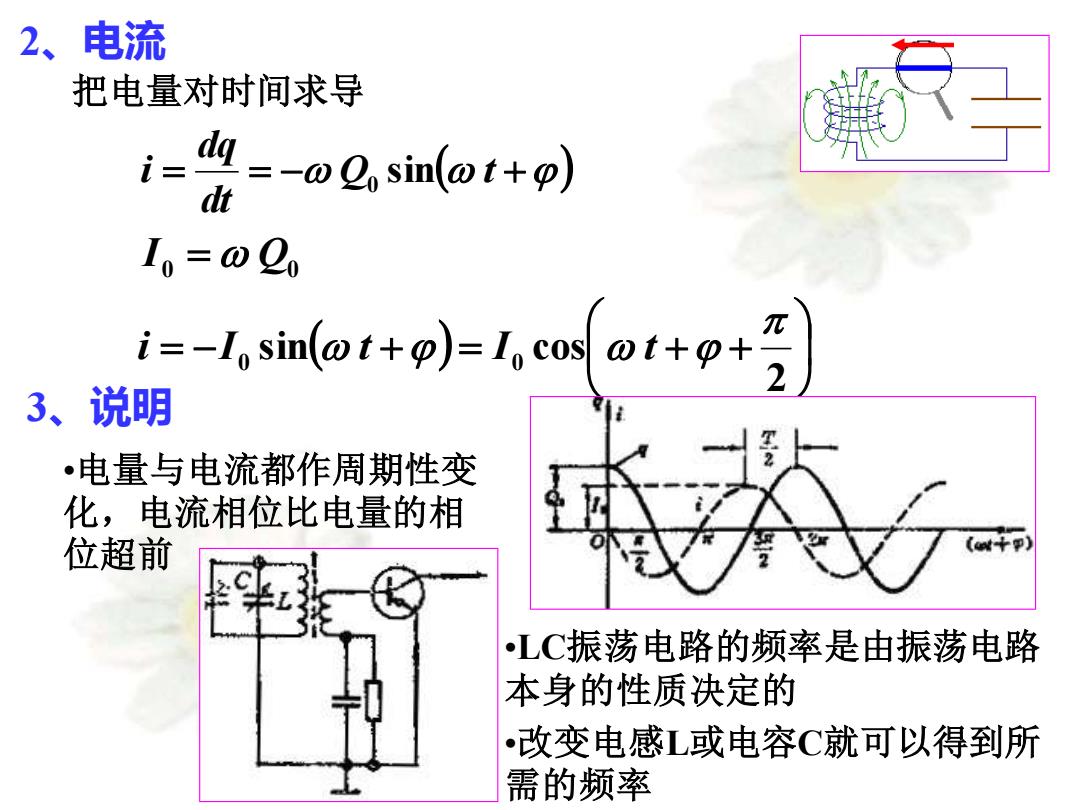
2、电流 把电量对时间求导 = = − Q ( t +) dt dq i 0 sin 0 Q0 I = ( ) = − + = + + 2 sin cos 0 0 i I t I t 3、说明 •电量与电流都作周期性变 化,电流相位比电量的相 位超前 •LC振荡电路的频率是由振荡电路 本身的性质决定的 •改变电感L或电容C就可以得到所 需的频率

三、无阻尼自由振荡的能量 1、电场能量 。=4=gcos@7+o C-2 2、磁场能量 Er=uismo+)gnlor+p) 3、总能量 E=E+E== 2C ·电场能量与磁场能量互相转化,但总能量保持不变。 无阻尼自由电磁振荡是理想化的模型,它要求: •电阻为零,不因为产生的焦耳热而损失电磁能; •不存在电动势,没有其他的能量转化为电磁能: ·电磁还不能以电磁波的形式辐射出去
三、无阻尼自由振荡的能量 1、电场能量 = = ( t +) C Q C q Ee cos 2 2 2 2 0 2 2、磁场能量 = = ( +) = ( t +) C Q E LI LI t m sin 2 sin 2 1 2 1 2 2 2 2 0 0 2 3、总能量 C Q E E E LI m e 2 2 1 2 2 0 = + = 0 = •电场能量与磁场能量互相转化,但总能量保持不变。 •无阻尼自由电磁振荡是理想化的模型,它要求: •电阻为零,不因为产生的焦耳热而损失电磁能; •不存在电动势,没有其他的能量转化为电磁能; •电磁还不能以电磁波的形式辐射出去

例题:已知LC电路中的电场能量与磁场能量之和为一常量, 试由此导出LC电路的振荡方程。 证:电场能量 E。=5CU2 2 磁场能量 Em=LI 2 E=E。+Em= ICU+L=const 1 将上式对求导,得 +LI=0 dt dt q=CU,I= dt dt d'U -U=0 dⅢ -c dt dr d0 41 d'U =0 2 2=0 IU+LIC
例题:已知LC电路中的电场能量与磁场能量之和为一常量, 试由此导出LC电路的振荡方程。 证:电场能量 2 2 1 Ee = CU 磁场能量 2 2 1 E LI m = E E E CU LI const = e + m = + = 2 2 2 1 2 1 将上式对t求导,得 + = 0 dt dI LI dt dU CU dt dU C dt dq q = CU,I = = 2 2 dt d U C dt dI = 0 2 2 + = dt d U IU LIC 0 1 2 2 U = dt LC d U + 0 1 2 2 Q = dt LC d Q +