
海大理学院教学裸件 大学物理学电子教案 波的衍射与干涉 15-3波的能量 15一4惠更斯原理波的衍射、反 射和折射 15一5波的干涉
大学物理学电子教案 海大理学院教学课件 波的衍射与干涉 15-3 波的能量 15-4 惠更斯原理 波的衍射、反 射和折射 15-5 波的干涉

复习 波动的基本概念 •横波和纵波 ·波长、波的周期和频率、波速 儿= 平面简谐波的波函数 y-Ac 波函数的物理意义
复 习 波动的基本概念 •横波和纵波 •波长、波的周期和频率、波速 = = T u •平面简谐波的波函数 = - + u x y Acos t •波函数的物理意义
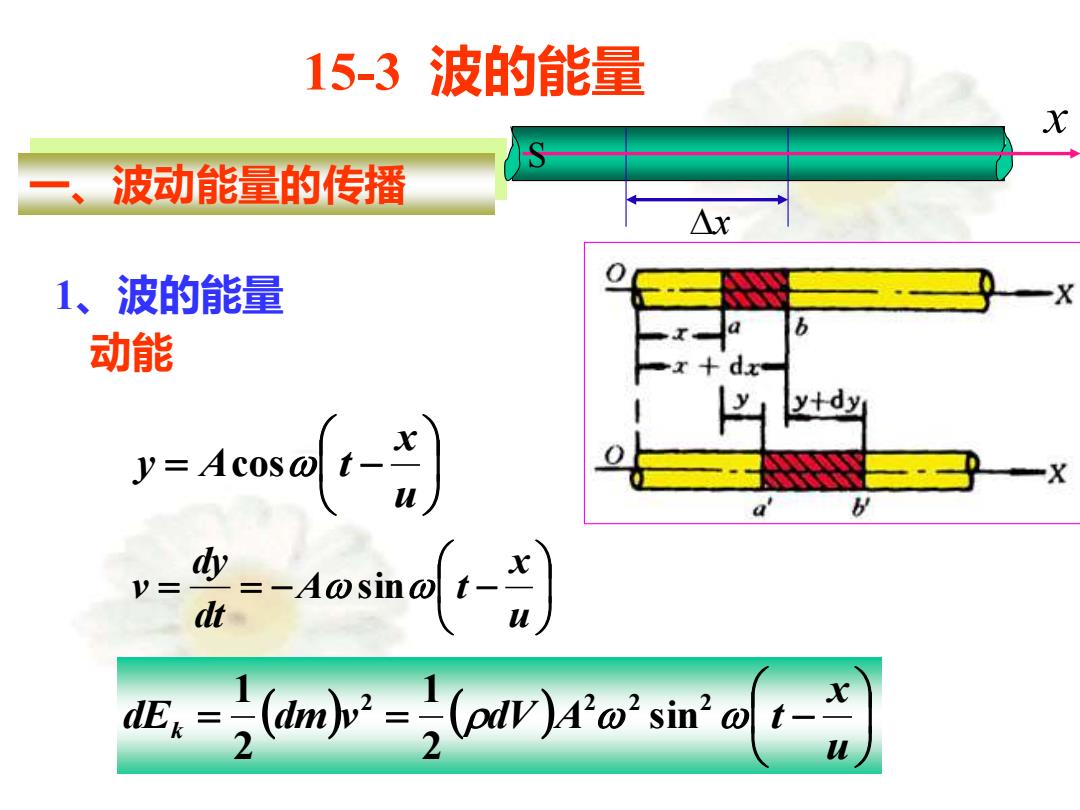
15-3 波的能量 波动能量的传播 △x 1、波的能量 动能 y+dy dE,=(dm)v=(odV)&o'sinot
15-3 波的能量 一、波动能量的传播 1、波的能量 动能 = − u x y Acos t = = − − u x A t dt dy v sin ( ) ( ) = = − u x dE dm v dV A t k 2 2 2 2 sin 2 1 2 1 x x S
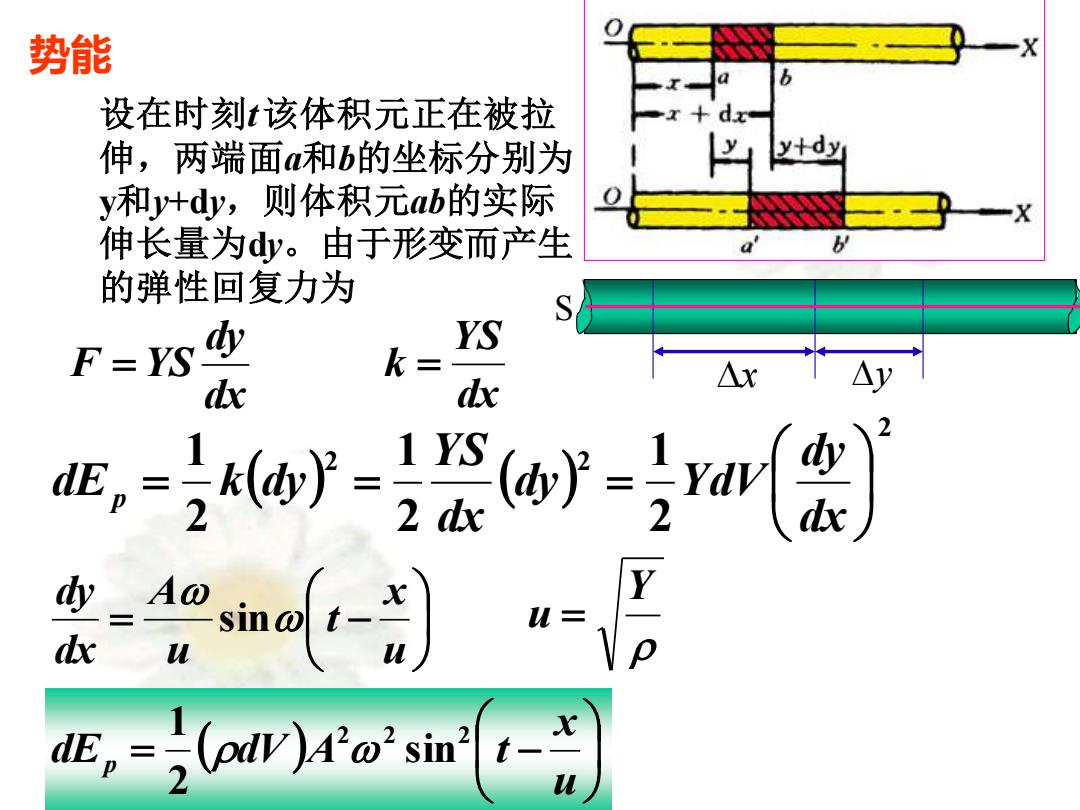
势能 设在时刻该体积元正在被拉 伸,两端面a和b的坐标分别为 y+dy y和y+dy,则体积元ab的实际 伸长量为dy。由于形变而产生 的弹性回复力为 S F=YS 西 YS k= dx d △y 2 2 dE,=,(oW))Ao2sin
势能 设在时刻t该体积元正在被拉 伸,两端面a和b的坐标分别为 y和y+dy,则体积元ab的实际 伸长量为dy。由于形变而产生 的弹性回复力为 dx dy F = YS dx YS k = ( ) ( ) 2 2 2 2 1 2 1 2 1 = = = dx dy dy YdV dx YS dE k dy p = − u x t u A dx dy sin Y u = ( ) = − u x dE dV A t p 2 2 2 sin 2 1 x y S
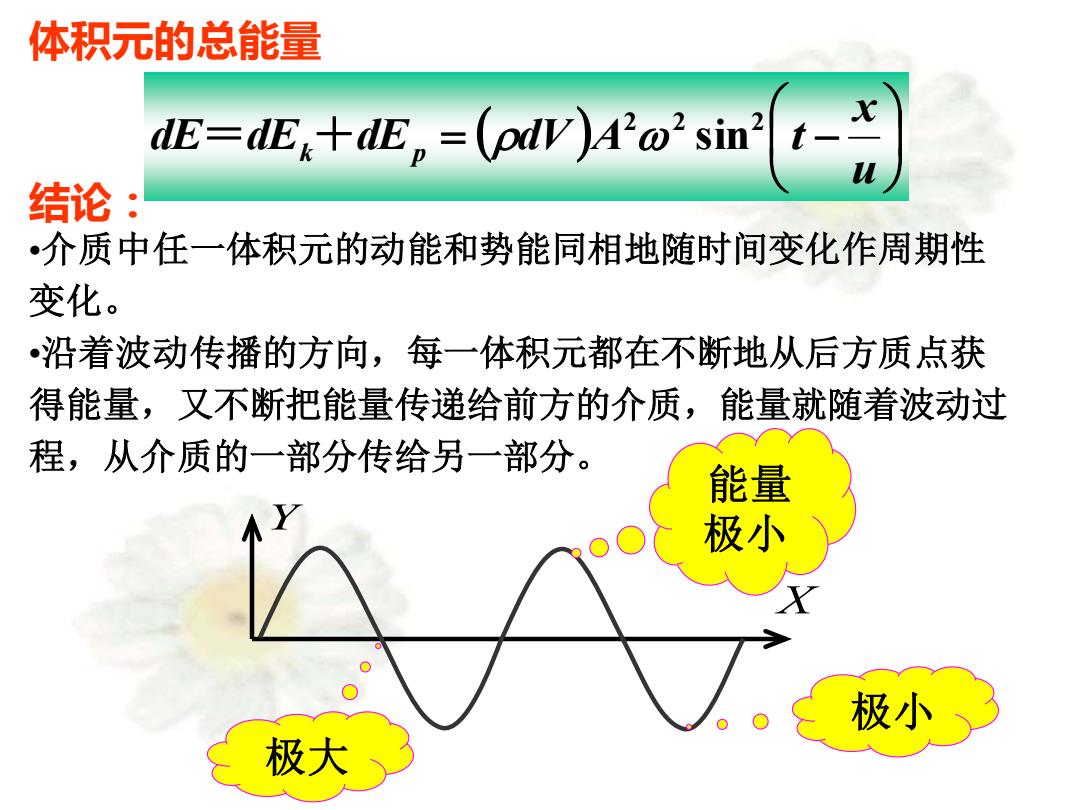
体积元的总能量 dE=dEx+dE,=(pdv)A'a2 sin2 结论 •介质中任一体积元的动能和势能同相地随时间变化作周期性 变化。 •沿着波动传播的方向,每一体积元都在不断地从后方质点获 得能量,又不断把能量传递给前方的介质,能量就随着波动过 程,从介质的一部分传给另一部分。 能量 极小 极小 极大
体积元的总能量 ( ) = − u x dE dE dE dV A t k p 2 2 2 = + sin 结论: •介质中任一体积元的动能和势能同相地随时间变化作周期性 变化。 •沿着波动传播的方向,每一体积元都在不断地从后方质点获 得能量,又不断把能量传递给前方的介质,能量就随着波动过 程,从介质的一部分传给另一部分。 X Y 极大 能量 极小 极小

2、波的能量密度 定义:单位体积介质中的能量就是能量密度 花=pois-周 平均能量密度一一个周期内的能量密度的平均值 osiw)
2、波的能量密度 定义:单位体积介质中的能量就是能量密度 − u x A t dV dE w 2 2 2 = = sin 平均能量密度——一个周期内的能量密度的平均值 2 2 0 2 2 2 2 1 sin 1 A dt u x A t T w T = − =
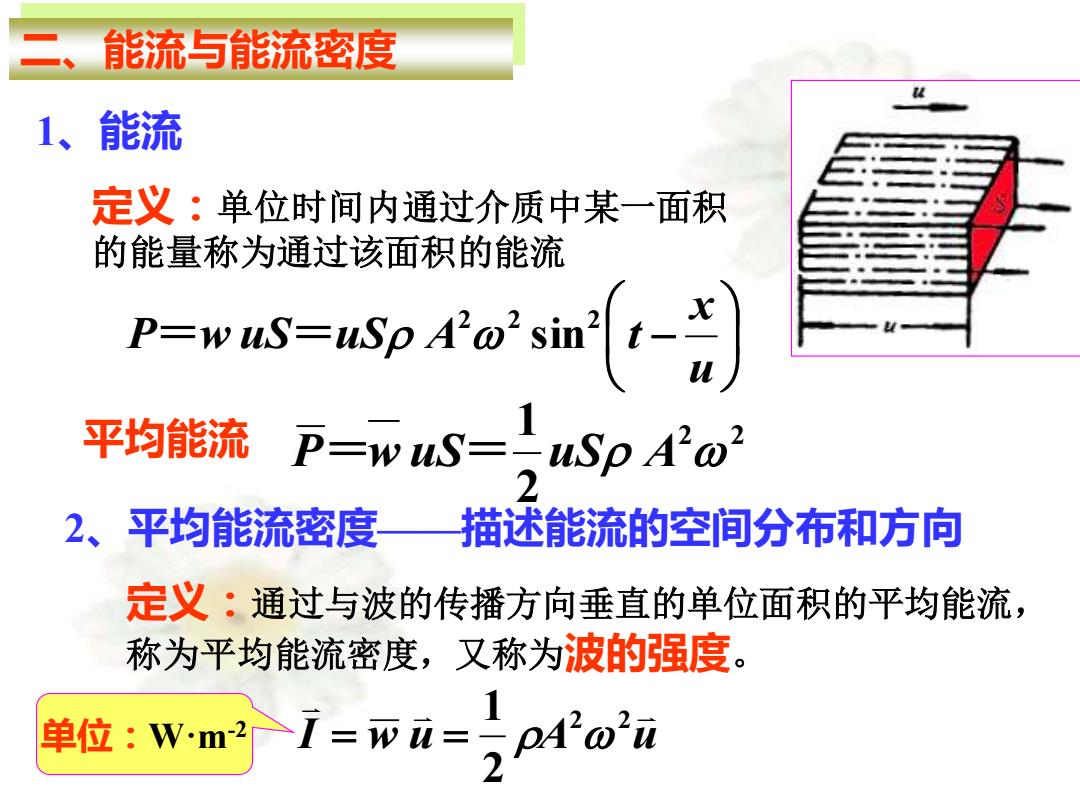
能流与能流密度 1、 能流 定义:单位时间内通过介质中某一面积 的能量称为通过该面积的能流 P=ww=ap4os气- 平均能流P=wS=。uSp A'a2 2、平均能流密度描述能流的空间分布和方向 定义:通过与波的传播方向垂直的单位面积的平均能流, 称为平均能流密度,又称为波的强度。 单位:Wm2 7=西三)212ω2z
二、能流与能流密度 1、能流 定义:单位时间内通过介质中某一面积 的能量称为通过该面积的能流 − u x P w uS uS A t 2 2 2 = = sin 平均能流 2 2 2 1 P=w uS= uS A 2、平均能流密度——描述能流的空间分布和方向 定义:通过与波的传播方向垂直的单位面积的平均能流, 称为平均能流密度,又称为波的强度。 I w u A u 2 2 2 1 单位:W·m-2 = =

例1、一球面波在均匀无吸收的介质中一波速u传播。在距离波 源r=1处质元的振幅为A。设波源振动的角频率为o,初相位 为零,试写出球面简谐波的表达式。 解:以点波源O以圆心作半径为和,的两 个球面,如图所示。由于介质不吸收波的 能量,因此,单位时间内通过球面的总平 均能量应该相等,即 41211=4m2212 An=A5 由于振动的相位随距离的增加而落后的 所以振幅与离波源的 关系,与平面波类似,球面简谐波的波 距离成反比。如果距 函数: 波源单位距离的振幅 A 为A,则距波源r处的 y=一 coso(t-- 振幅为A/r
1 r 2 r 由于振动的相位随距离的增加而落后的 关系,与平面波类似,球面简谐波的波 函数: cos ( ) u r t r A y = − 解:以点波源O以圆心作半径为r1和r2的两 个球面,如图所示。由于介质不吸收波的 能量,因此,单位时间内通过球面的总平 均能量应该相等,即 所以振幅与离波源的 距离成反比。如果距 波源单位距离的振幅 为A,则距波源r处的 振幅为A/ r 例1、一球面波在均匀无吸收的介质中一波速u传播。在距离波 源r1=1m处质元的振幅为A。设波源振动的角频率为ω ,初相位 为零,试写出球面简谐波的表达式。 2 2 1 2 2 4r1 I = 4r I I A u 2 1 2 1 2 1 = I A u 2 2 2 2 2 1 = 1 1 2 2 A r = A r

例2、一列余弦波沿直径为0.14m的圆柱形玻璃管前进,波的 平均强度为18×103Js1m-2,频率为300Hz,波速为300ms 1。 求 ①波中的平均能量密度和最大能量密度; ②位相差为2的相邻两个截面间的能量。 解:①平均能量密度 w= 118×10-3 =6×10-5J.m-3 300 w=pYws[ou-点+可 wmax=p42o2=2w=12×10-5J.m3 ②位相差为2π间距离为一个波长) =300 =1m 300 W=wS九=6×10-5×0.072π×1=9.2×10-7J
例 2、 一列余弦波沿直径为 0.14 m 的圆柱形玻璃管前进 , 波的 平均强度为 18×10-3 J s -1 m –2 , 频率为 300 Hz , 波速为 300 m s – 1 。求 ① 波中的平均能量密度和最大能量密度; ② 位相差为 2π的相邻两个截面间的能量。 解: ① 平均能量密度 5 3 3 6 10 300 18 10 − − − = = = J m u I w = sin ( − )+ 2 2 2 u x w A t 2 2 5 3 max 2 12 10− − w = A = w = J m ② 位相差为 2π间距离为一个波长λ m u 1 300 300 = = = W wS J 5 2 7 6 10 0.07 1 9.2 10 − − = = =

15-4惠更斯原理波的行射、反射和折射 惠更斯:(Christian Haygens,1629-1695) 荷兰物理学家、数学家、天文学家。 1629年出生于海牙。1655年获得法学博 士学位。1663年成为伦敦皇家学会的第 一位外国会员。 他的重要贡献有: ①建立了光的波动学说,打破了当时流行的光的微粒学说,提 出了光波面在媒体中传播的惠更斯原理。 ②1673年他解决了物理摆的摆动中心问题,测定了重力加速度 之值,改进了摆钟,得出了离心力公式,还发明了测微计。 ③他发现了双折射光束的偏振性,并用波动观点作了解释。 ④在天文学方面,他供助自已设计和制造的望远镜于1665年, 发现了土星卫星土卫六,且观察到了土星环
15-4 惠更斯原理 波的衍射、反射和折射 惠更斯: (Christian Haygens,1629—1695) 荷兰物理学家、数学家、天文学家。 1629年出生于海牙。1655年获得法学博 士学位。1663年成为伦敦皇家学会的第 一位外国会员。 他的重要贡献有: ①建立了光的波动学说,打破了当时流行的光的微粒学说,提 出了光波面在媒体中传播的惠更斯原理。 ②1673年他解决了物理摆的摆动中心问题,测定了重力加速度 之值,改进了摆钟,得出了离心力公式,还发明了测微计。 ③他发现了双折射光束的偏振性,并用波动观点作了解释。 ④在天文学方面,他供助自己设计和制造的望远镜于1665年, 发现了土星卫星----土卫六,且观察到了土星环