
海大理学院表号裸件 大学物理学电子教案 静电场中的电介质2 9一5静电场的能量能量密度 9一6静电的应用 9一7电场的边界条件 9一8压电效应铁电体驻极体
大学物理学电子教案 海大理学院教学课件 静电场中的电介质2 9-5 静电场的能量 能量密度 9-6 静电的应用 9-7 电场的边界条件 9-8 压电效应 铁电体 驻极体

复习 静电场中的电介质 i=fo 电位移 D=50E+P=EE 电介质中的高斯定理 月D.s=g
复 习 •静电场中的电介质 r E E 0 = D E P r E = + = 0 D dS Q S = •电位移 •电介质中的高斯定理

9-5静电场的能量1 能量密度 电容器的电能 设在某时刻两极板之间的电势差为U, 此时若把+dg电荷从带负电的负极板 搬运到带正电的正极板,外力所作的 功为 dW Udg=1 dq 若使电容器的两极板分别带有士Q的电荷,则外力所作的功为 W- 2C 20w-cw2 电容器所储存的静电能 外力克服静电场力作功, 把非静电能转换为带电 W CU2 体系的静电能 2C1
9-5 静电场的能量 能量密度 一、电容器的电能 设在某时刻两极板之间的电势差为U, 此时若把+dq电荷从带负电的负极板 搬运到带正电的正极板,外力所作的 功为 E +dq + _ dq C q dW = Udq = 若使电容器的两极板分别带有±Q的电荷,则外力所作的功为 2 2 0 2 1 2 1 2 Q U CU C Q dq C q W Q = = = = 电容器所储存的静电能 2 2 2 1 2 CU C Q We = = 外力克服静电场力作功, 把非静电能转换为带电 体系的静电能

静电场的能量能量密度 1、静电场的能量 对于极板面积为S、极板间距为平板电容器,电场所 占的体积为Sd,电容器储存的静电能为 2 d 电容器所具有的能量与极板间电场E和D有关,E和D是极板 间每一点电场大小的物理量,所以能量与电场存在的空间有 关,电场携带了能量。 2、电场的能量密度 定义:单位体积内的能量 0。 对于任意电场,本结论都是成立的
二、静电场的能量 能量密度 1、静电场的能量 对于极板面积为S、极板间距为d平板电容器,电场所 占的体积为Sd,电容器储存的静电能为 (Ed) SE d d S We CU2 2 2 2 1 2 1 2 1 = = = 2、电场的能量密度 定义:单位体积内的能量 2 2 1 e = E 对于任意电场,本结论都是成立的。 电容器所具有的能量与极板间电场E和D有关,E和D是极板 间每一点电场大小的物理量,所以能量与电场存在的空间有 关,电场携带了能量
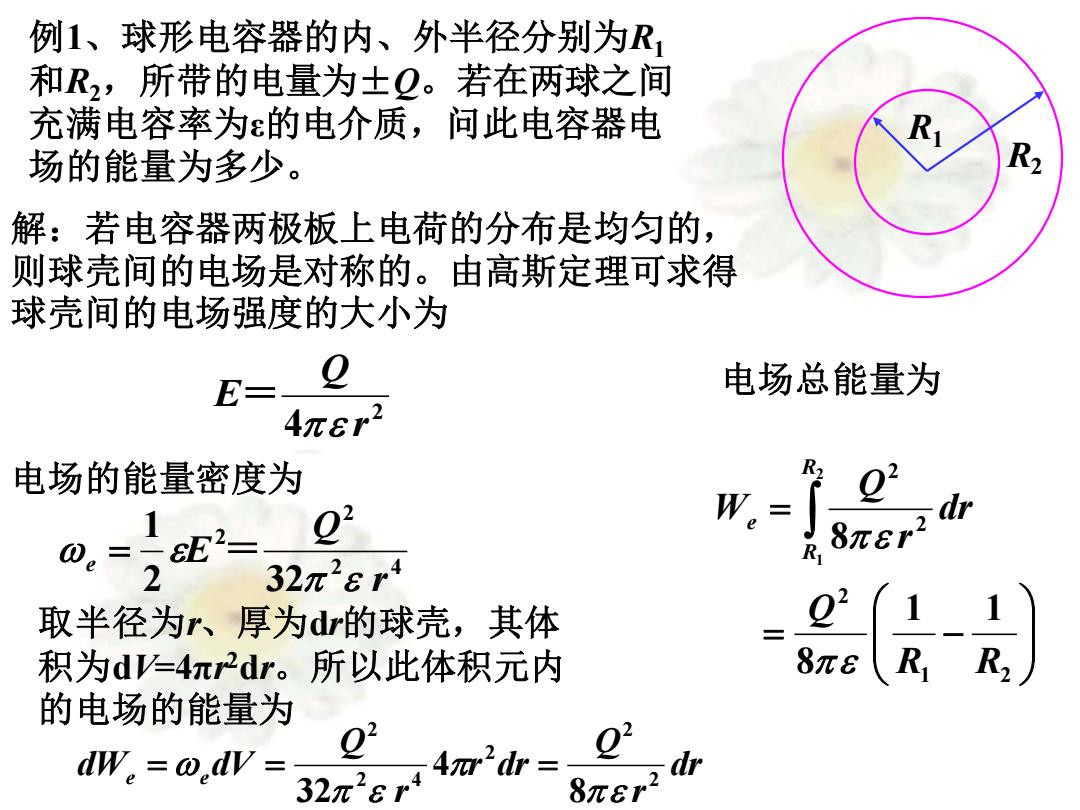
例1、球形电容器的内、外半径分别为R, 和R2,所带的电量为士9。若在两球之间 充满电容率为ε的电介质,问此电容器电 场的能量为多少。 解:若电容器两极板上电荷的分布是均匀的, 则测球壳间的电场是对称的。由高斯定理可求得 球壳间的电场强度的大小为 E= 电场总能量为 4r8r2 电场的能量密度为 w.=[ dr 2 32π2εr4 取半径为r厚为dr的球壳,其体 =0' 1 积为d=4πr2dr。所以此体积元内 8π8 R R, 的电场的能量为 dW。=o.dV= 42d= 32π2er4 8πr2
例1、球形电容器的内、外半径分别为R1 和R2,所带的电量为±Q。若在两球之间 充满电容率为ε的电介质,问此电容器电 场的能量为多少。 R1 R2 解:若电容器两极板上电荷的分布是均匀的, 则球壳间的电场是对称的。由高斯定理可求得 球壳间的电场强度的大小为 2 4 r Q E = 电场的能量密度为 2 4 2 2 2 32 1 r Q e E = = 取半径为r、厚为dr的球壳,其体 积为dV=4πr 2dr。所以此体积元内 的电场的能量为 dr r Q r dr r Q dWe e dV 2 2 2 2 4 2 8 4 32 = = = 电场总能量为 = − = 1 2 2 2 2 1 1 8 8 2 1 R R Q dr r Q W R R e

例2、一个球半径为R,体电荷密度为P,试利用电场能量公式 求此带电球体系统的静电能。 r≤R 380B, PR3 r≥R -∫mv-∫2v or' 2 2 ne(pr )4u'dr2 2388, )'dr Anp Rs AnpiRAnp Ri 5×18608,18eo6, 158o8r
例2、一个球半径为R,体电荷密度为,试利用电场能量公式 求此带电球体系统的静电能。 R r r R r E r = ˆ 3 0 1 r r R r R E r = ˆ 3 2 0 3 2 = = dV E W w dV r e 2 2 0 = + R r R r r dr E r dr E 2 2 0 2 0 2 2 0 1 4 2 4 2 = + R r r R r r r dr r R r dr r 2 2 2 0 3 0 0 2 2 0 0 ) 4 3 ( 2 ) 4 3 ( 2 r r R R 0 2 5 0 2 5 18 4 5 18 4 + = r R 0 2 5 15 4 =

9-6静电的应用 静电的特点 •带电体所带的静电电荷的电量都很小; 静电场所具有的能量也不大; •电压可能很高。 静电的应用 •范德格拉夫起电机 •静电除尘 静电分离 •静电织绒 •静电喷漆 静电消除器 静电生物技术 Figure 18.6 Electropainting is standard technology in automo- bile manufacturing.The body of the car and the paint are given op posite charges,so that the electrostatic force of attraction causes the paint to cover the body more thoroughly
9-6 静电的应用 一、静电的特点 •带电体所带的静电电荷的电量都很小; •静电场所具有的能量也不大; •电压可能很高。 二、静电的应用 •范德格拉夫起电机 •静电除尘 •静电分离 •静电织绒 •静电喷漆 •静电消除器 •静电生物技术
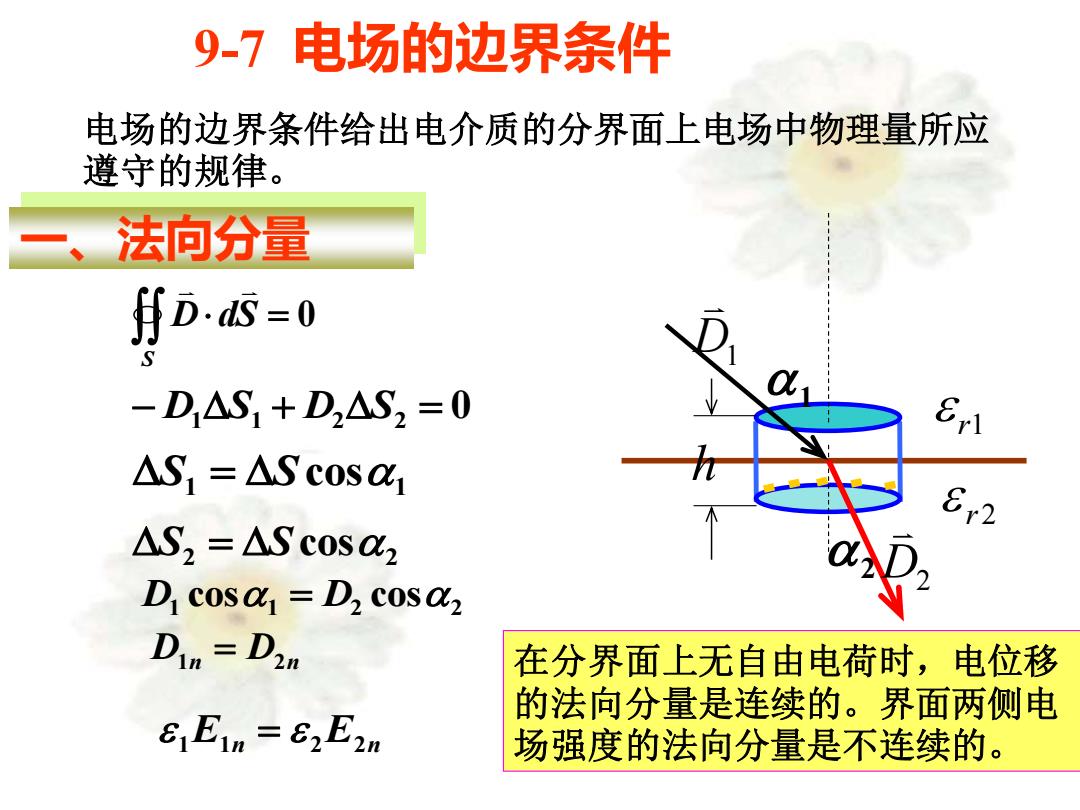
9-7电场的边界条件 电场的边界条件给出电介质的分界面上电场中物理量所应 遵守的规律。 法向分量 月Ds=0 -D△S1+D2△S2=0 △S1=△Sc0Sa1 2 △S2=△Sc0sa2 D cosa=D>cosa Di=D2n 在分界面上无自由电荷时,电位移 的法向分量是连续的。界面两侧电 EIn=82E2n 场强度的法向分量是不连续的
9-7 电场的边界条件 电场的边界条件给出电介质的分界面上电场中物理量所应 遵守的规律。 r1 r 2 h 2 1 D1 D2 一、法向分量 = 0 S D dS − D1 S1 + D2 S2 = 0 1 1 S = Scos 2 2 S = Scos 1 1 2 2 D cos = D cos D1n = D2n 1 E1n 2 E2n = 在分界面上无自由电荷时,电位移 的法向分量是连续的。界面两侧电 场强度的法向分量是不连续的
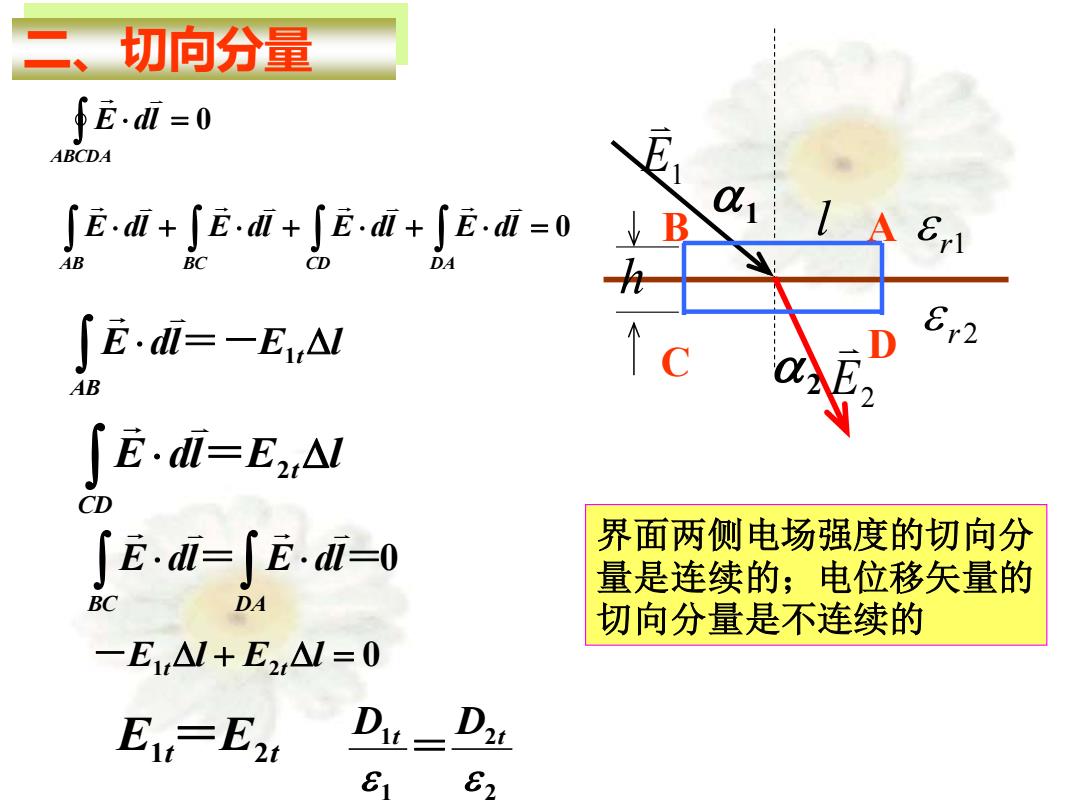
切向分量 fE.di-0 ABCDA ∫E.i+∫E.+∫Ei+∫Ei=0 B D ∫E·i=-E△M AB ∫E.di=E2△l CD ∫Edi=∫E.di=0 界面两侧电场强度的切向分 量是连续的;电位移矢量的 DA 切向分量是不连续的 -E,△M+E2,△1=0 E1=E2 81 82
r1 r 2 1 2 E1 E2 h l 二、切向分量 = ABCDA E dl 0 B A C D + + + = 0 AB BC CD DA E dl E dl E dl E dl E dl E l t AB =- 1 E dl E l t CD = 2 = =0 BC DA E dl E dl -E1t l + E2t l = 0 E1t =E2t 2 2 1 1 D t = D t 界面两侧电场强度的切向分 量是连续的;电位移矢量的 切向分量是不连续的

9-8 压电效应铁电体驻极体 压电效应 压电效应(正压电效应):某些固体电介质,当它们发生机械形 变时,会产生极化,在它们相对的两个面上将产生异号的极化 电荷。这种因机械形变而产生的电极化现象称为压电效应。 •电致伸缩(逆压电效应):在电场的作用下,晶体发生机械形变。 应用: 机械振荡→电振荡:送话器、电唱针、测量爆炸时的压力 电振荡→机械振荡:超声波的换能器 铁电体 ·概念:酞酸钡等电介质的相对电容率很大,且随外加电 场而改变;当外加电场撤去以后,电介质并不称为中性, 而具有剩余极化,这一性质与铁磁质很相似,称为铁电体。 应用:制造电容器和各种压电器件
9-8 压电效应 铁电体 驻极体 一、压电效应 •压电效应(正压电效应):某些固体电介质,当它们发生机械形 变时,会产生极化,在它们相对的两个面上将产生异号的极化 电荷。这种因机械形变而产生的电极化现象称为压电效应。 •电致伸缩(逆压电效应):在电场的作用下,晶体发生机械形变。 •应用: 机械振荡→电振荡:送话器、电唱针、测量爆炸时的压力 电振荡→机械振荡:超声波的换能器 二、铁电体 •概念:酞酸钡等电介质的相对电容率很大,且随外加电 场而改变;当外加电场撤去以后,电介质并不称为中性, 而具有剩余极化,这一性质与铁磁质很相似,称为铁电体。 •应用:制造电容器和各种压电器件