
海大理学院教学裸件 大学物理学电子教案 安培力与磁力矩 11-6载流导线在磁场中所受的力 11-7磁场对载流线圈的作用
大学物理学电子教案 海大理学院教学课件 安培力与磁力矩 11-6 载流导线在磁场中所受的力 11-7 磁场对载流线圈的作用

复习 ·带电粒子在磁场中所受的力一洛伦兹力 Fm=qd×B m 带电粒子在磁场中的运动 速度方向与磁场方向平行一直线运动 垂直—圆周运动 有夹角—螺旋运动 •速度选择器 •霍耳效应一现象、规律、理论解释和应用
复 习 •带电粒子在磁场中所受的力——洛伦兹力 Fm qv B = •带电粒子在磁场中的运动 速度方向与磁场方向平行——直线运动 垂直——圆周运动 有夹角——螺旋运动 •速度选择器 •霍耳效应——现象、规律、理论解释和应用
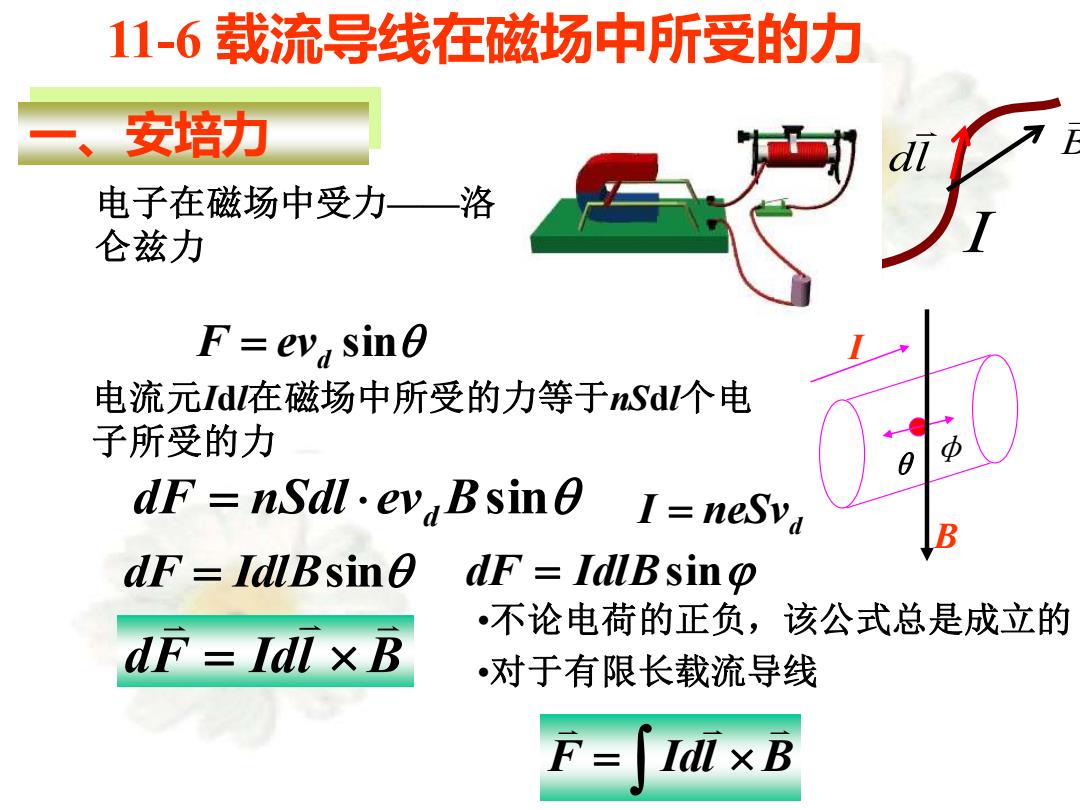
11-6载流导线在磁场中所受的力 安培力 电子在磁场中受力—洛 仑兹力 F=eva sin 电流元Id在磁场中所受的力等于Sd个电 子所受的力 dF nSdl.ev BsinO I=neSva dF IdlBsinO dF IdlBsino 不论电荷的正负,该公式总是成立的 dF=Idi×B •对于有限长载流导线 F= Id×B
11-6 载流导线在磁场中所受的力 一、安培力 电子在磁场中受力——洛 仑兹力 F = evd sin dl B I B I θφ 电流元Idl在磁场中所受的力等于nSdl个电 子所受的力 dF = nSdl evd Bsin neSvd I = dF = IdlBsin dF = IdlBsin dF Idl B = •不论电荷的正负,该公式总是成立的 •对于有限长载流导线 F = Idl B

例题1、有一段弯曲导线b通有电流1,求此导线在如图所示 均匀磁场中受的力? F=Idi×B F=(0)×B F=几×B F=IIBsin0 与磁感应强度B在同一平面内,所以,该 力方向垂直于纸面向外
例题1、有一段弯曲导线ab 通有电流I ,求此导线在如图所示 均匀磁场中受的力? F I dl B b a = ( ) F = IlBsin l dl B a b = b a F Idl B l与磁感应强度B在同一平面内,所以,该 力方向垂直于纸面向外。 F Il B =
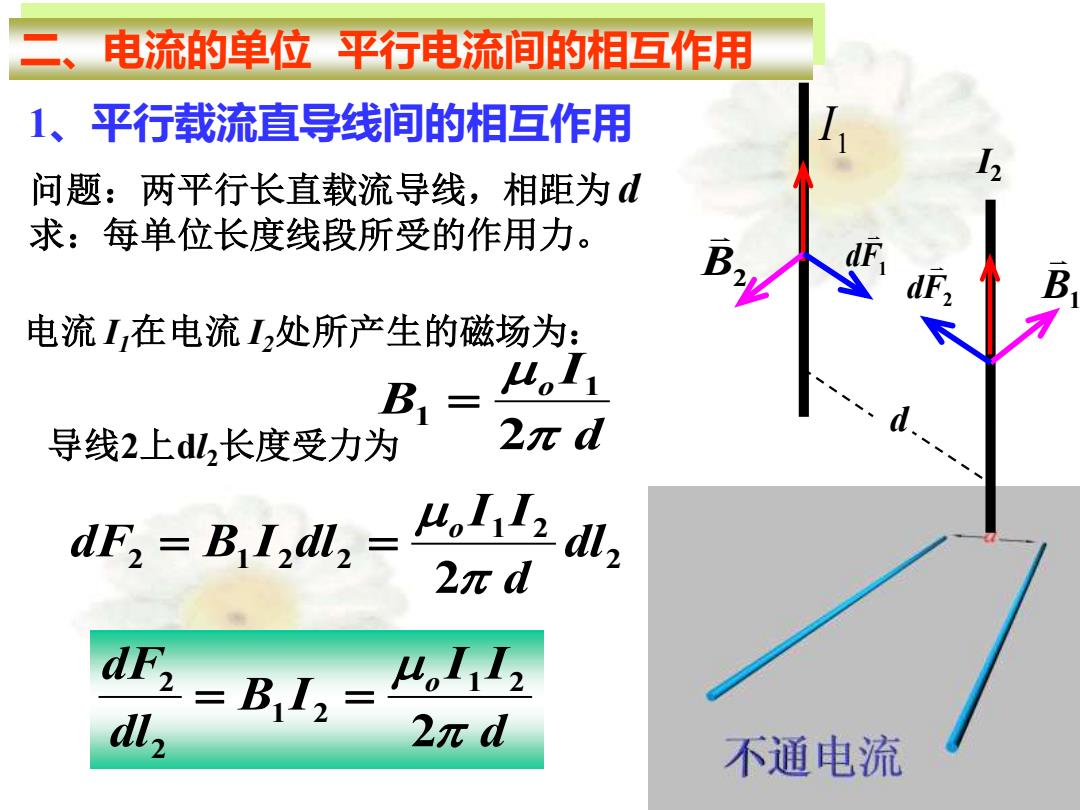
电流的单位平行电流间的相互作用 1、平行载流直导线间的相互作用 问题:两平行长直载流导线,相距为d 求:每单位长度线段所受的作用力。 电流1,在电流I,处所产生的磁场为: B1= 4o1 导线2上dL,长度受力 2πd d,=Bl,d,=,5 2πd =BL,=4马 2πd 不通电流
二、电流的单位 平行电流间的相互作用 d I B o 2 1 1 = 电流 I1在电流 I2处所产生的磁场为: 问题:两平行长直载流导线,相距为 d 求:每单位长度线段所受的作用力。 2 1 2 2 1 2 2 2 dl d I I dF B I dl o = = 导线2上dl2长度受力为 1、平行载流直导线间的相互作用 d I I B I dl dF o 2 1 2 1 2 2 2 = = B1 F2 d 1 I F1 d B2 d I2

电流I,在电流I,处所产生的磁场为: B2= 4L2 2x d S=A,1叫=-a 2πd dF == 4。I2 dl, 2n d 2、电流强度的单位: 在其空中有两根平行的长直线,它们之间相距1m,两导线上电 流流向相同,大小相等,调节它们的电流,使得两导线每单位 长度上的吸引力为2×10N·m1,我们就规定这个电流为1A
2、电流强度的单位: 在其空中有两根平行的长直线,它们之间相距1m,两导线上电 流流向相同,大小相等,调节它们的电流,使得两导线每单位 长度上的吸引力为2×10-7N· m-1,我们就规定这个电流为1A。 d I B o 2 2 2 = 1 2 1 1 2 1 1 2 dl d I I dF B I dl o = = 电流 I2在电流 I1 处所产生的磁场为: d I I B I dl dF o 2 2 1 2 1 1 1 = = B1 F2 d 1 I F1 d B2 d I2
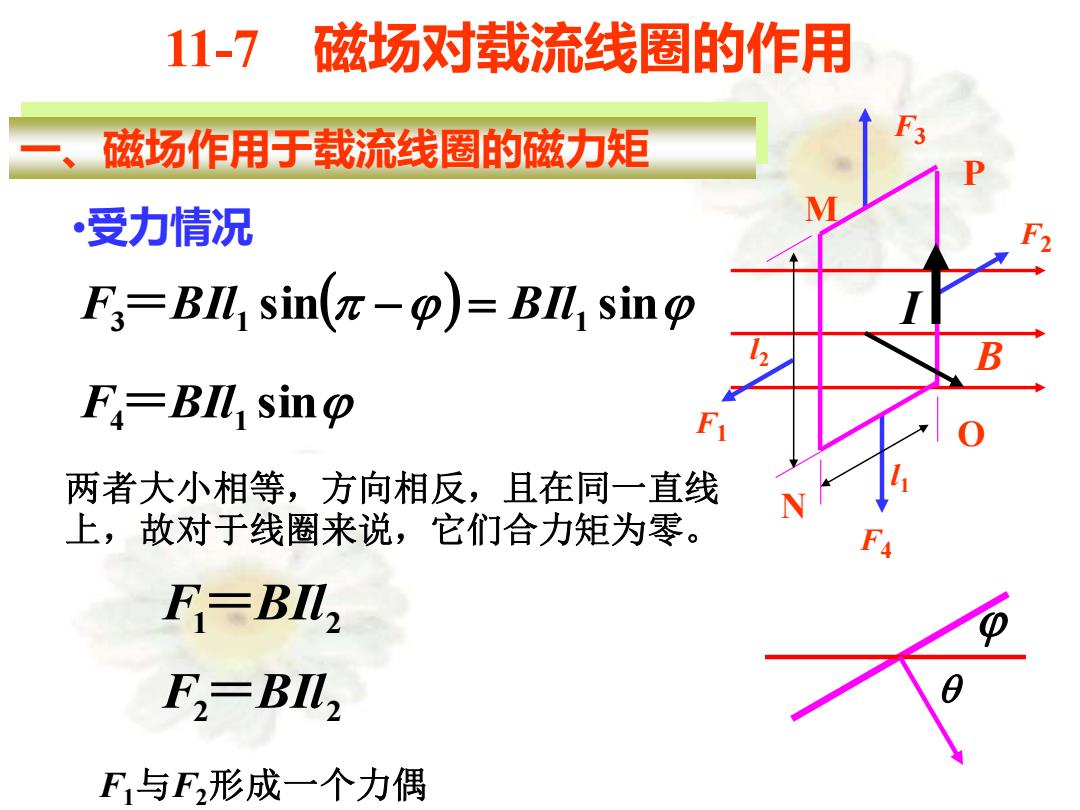
11-7 磁场对载流线圈的作用 磁场作用于载流线圈的磁力矩 受力情况 F:=BIL sin(-p)=BI sino F-BI sinp 两者大小相等,方向相反,且在同一直线 上,故对于线圈来说,它们合力矩为零。 F=BIL, F,=BI F与F形成一个力偶
11-7 磁场对载流线圈的作用 一、磁场作用于载流线圈的磁力矩 •受力情况 F1 =BIl2 F2 =BIl2 B F4 F3 F1 F2 l1 l2 M N O P I F3 =BIl1 sin( −) = BIl1 sin F4 =BIl1 sin 两者大小相等,方向相反,且在同一直线 上,故对于线圈来说,它们合力矩为零。 F1与F2形成一个力偶

•线圈所受有磁力矩 M=FI cos M-FI cos0 BIl,l sine BIS sin0 N 引入磁矩 M=m×B 讨论: 0=π2,线圈与磁场平行, 磁通量D=0,力矩Mmax=lSB 0=0, 垂直, Φ=BS,力矩M=0,平衡 0=, 垂直, Φ=-BS,力矩M=0,平衡
•线圈所受有磁力矩 M=F1 l 1 cos sin sin cos 2 1 1 1 BIS BIl l M F l = = = M m B = 引入磁矩 •讨论: =/2,线圈与磁场平行,磁通量F =0,力矩Mmax =ISB =0, 垂直, F =BS,力矩M=0,平衡 =, 垂直, F =-BS,力矩M=0,平衡
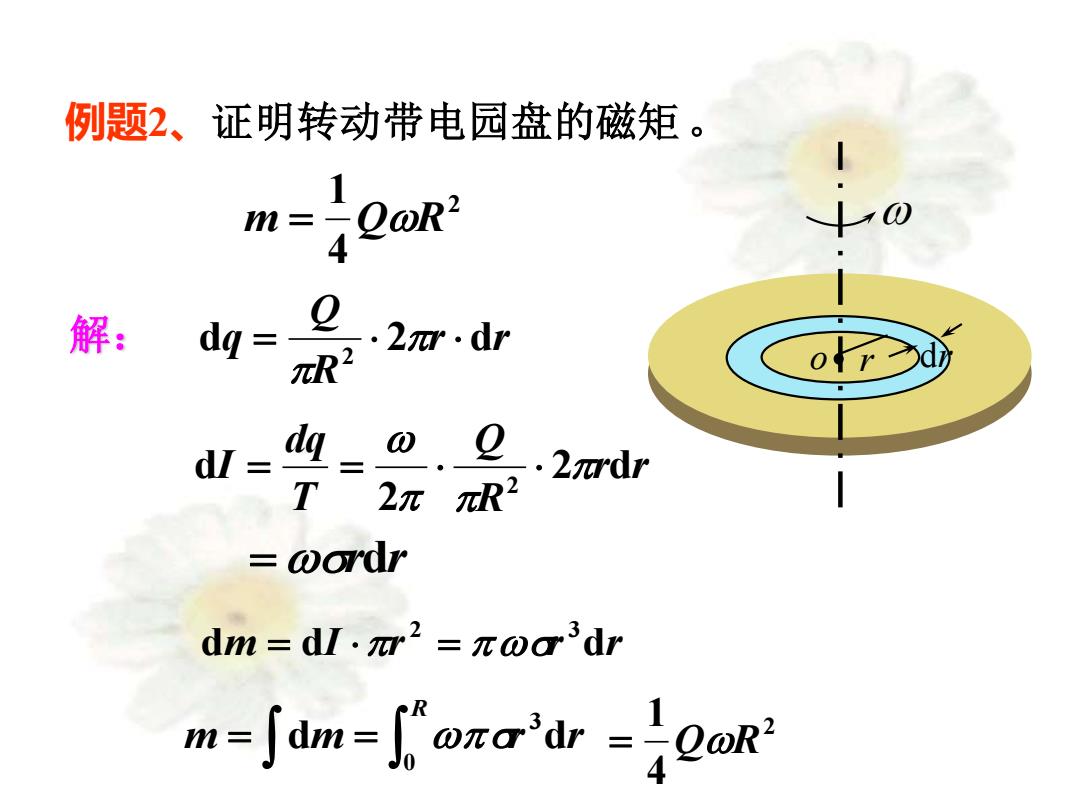
例题2、证明转动带电园盘的磁矩。 m-QoR 1 A0 解: dg 卫.·2m.d AR dI 2nrdr T 2R2 wordr dm=d·m2=πoa3dr m=∫dm=wrad=2oR2
例题2、证明转动带电园盘的磁矩。 2 4 1 m = QR r dr o r r R Q dq 2 d 2 = 解: r r R Q T dq I 2 d 2 d 2 = = =rdr dm dI r r dr 2 3 = = = = R m m r r 0 3 d d 2 4 1 = QR
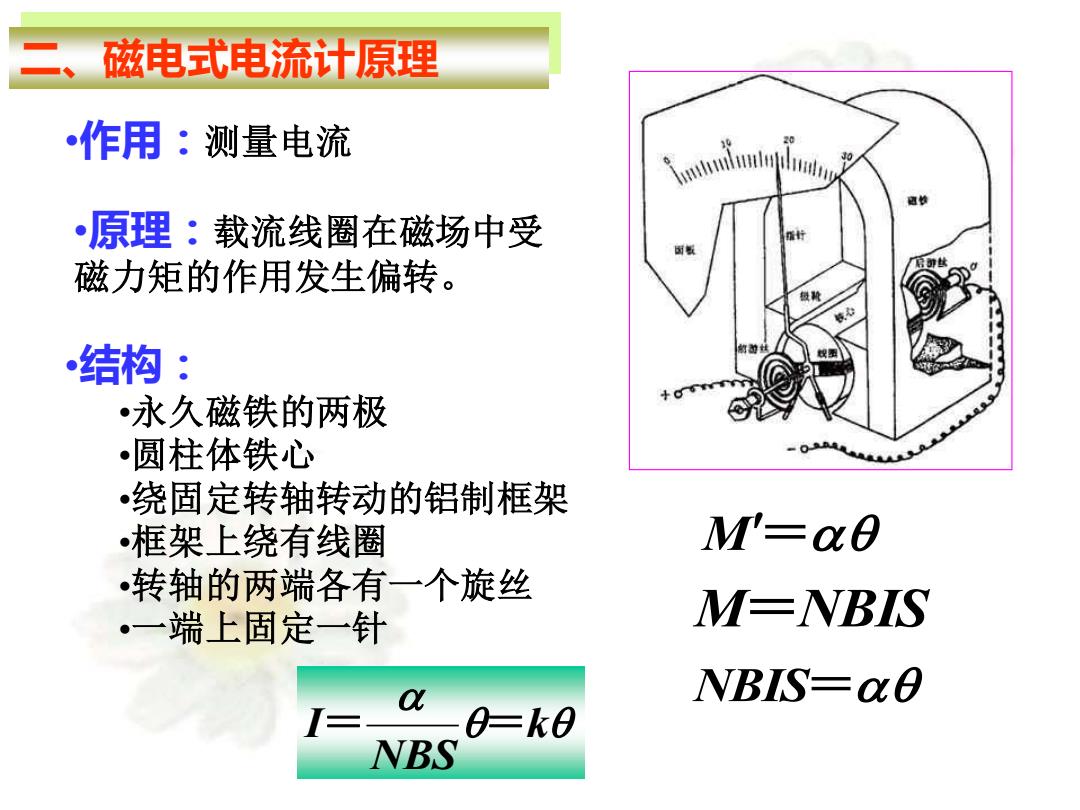
二、 磁电式电流计原理 作用:测量电流 0 Anwullhw ·原理:载流线圈在磁场中受 磁力矩的作用发生偏转。 结构: •永久磁铁的两极 圆柱体铁心 绕固定转轴转动的铝制框架 •框架上绕有线圈 M'-a0 ·转轴的两端各有一个旋丝 。一端上固定一针 M-NBIS q NBIS-q0 0=k0 NBS
二、磁电式电流计原理 •作用:测量电流 •原理:载流线圈在磁场中受 磁力矩的作用发生偏转。 •结构: •永久磁铁的两极 •圆柱体铁心 •绕固定转轴转动的铝制框架 •框架上绕有线圈 •转轴的两端各有一个旋丝 •一端上固定一针 M=NBIS NBIS= M= k NBS I= =