
海大理学院教学裸件 大学物理学电子教案 驻波、声波和多普勒效应 15-6驻波 15-7声波、超声波、次声波 15-8多普勒效应
大学物理学电子教案 海大理学院教学课件 驻波、声波和多普勒效应 15-6 驻波 15 -7 声波、超声波、次声波 15 - 8 多普勒效应

复习 •波动能量 能量密度 d-pda 平均能流密度 1-wu-zpfon •惠更斯原理 •惠更斯原理解释波的衍射、反射和折射 波的叠加原理 波的干涉 △p=±2kπ, k=0,1,2,… △0=±(2k-1)π, k=1,2,3
复习 •波动能量 − u x A t dV dE w 2 2 2 能量密度 = = sin 平均能流密度 I w u A u 2 2 2 1 = = •惠更斯原理 •惠更斯原理解释波的衍射、反射和折射 •波的叠加原理 •波的干涉 = 2k , k = 0,1,2,... = (2k −1) , k = 1,2,3
15-6 驻波 驻波的产生 1、演示实验: 弦线上的驻波 D 演示 分别沿X轴正、负方向传播的同频率、同初 相位的两列相干波,其合成波某些点振幅特 大,某些点几乎不动,称为驻波 y 波节 2、驻波的形成 驻波是一种特殊的干涉现象。 波节—静止不动, 振幅为零 波腹 —振动最强, 振幅最大 美0美 波腹
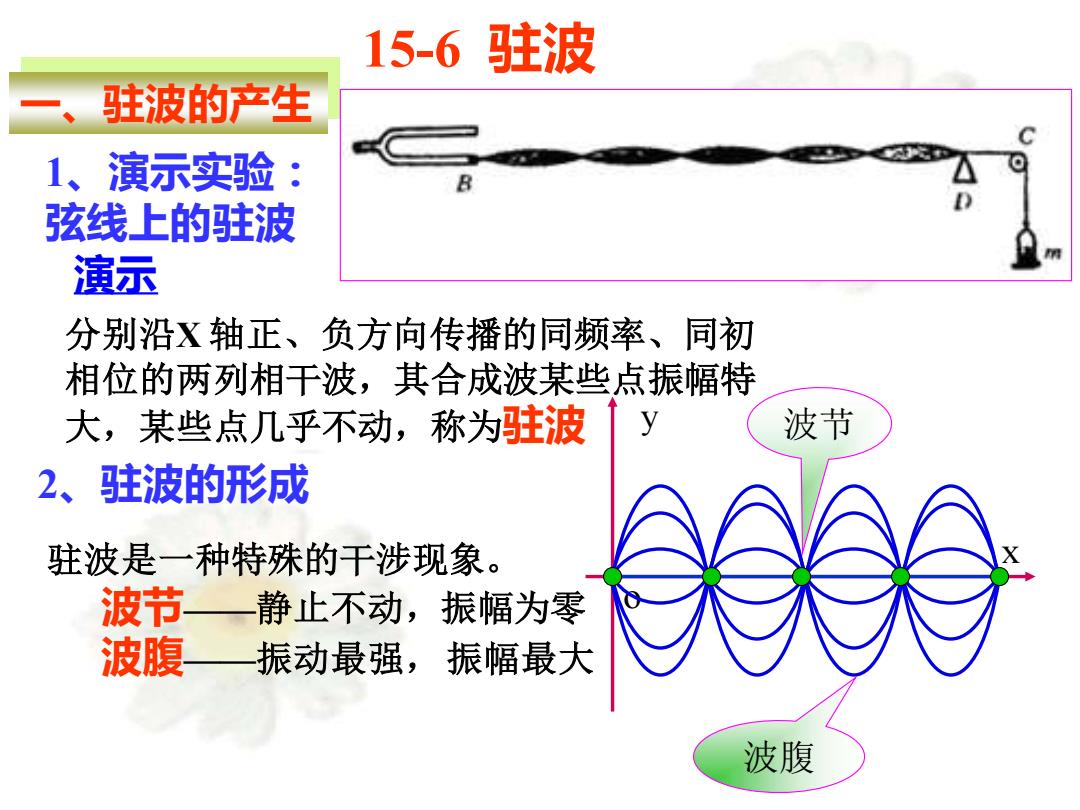
分别沿X 轴正、负方向传播的同频率、同初 相位的两列相干波,其合成波某些点振幅特 大,某些点几乎不动,称为驻波 15-6 驻波 一、驻波的产生 1、演示实验: 弦线上的驻波 演示 2、驻波的形成 驻波是一种特殊的干涉现象。 波节——静止不动,振幅为零 波腹——振动最强,振幅最大 x y o 波节 波腹

驻波方程 1、 驻波方程 t=0 设沿X轴正方向和负方向传播的 两列相干波的表达式为 =4w2-别 y2t=0 =As2w+ 其合成波为: t,=4s2w-Ao2+ 2 y=2Acos2r-c0S2πt 演示 该式由两项组成:一项 只与位置有关,称为 它表示各点都在作简谐振动,各点振动 振幅因子,一项只与 的频率相同,是原来波的频率。但各点 时间有关,称为简谐 振幅随位置的不同而不同。 振动因子
设沿X轴正方向和负方向传播的 两列相干波的表达式为 二、驻波方程 t = 0 x x = 0 2 t = 0 y x x = 0 1 y 其合成波为: = + = − x y A t x y A t cos 2 cos 2 2 1 + = = − x A t x y y1 +y2 Acos 2 t + cos 2 1、驻波方程 它表示各点都在作简谐振动,各点振动 的频率相同,是原来波的频率。但各点 振幅随位置的不同而不同。t x y A = 2 cos2 cos2 该式由两项组成:一项 只与位置有关,称为 振幅因子,一项只与 时间有关,称为简谐 振动因子。 演示

2、 波节和波腹 …概念 满足cos(2πx/)的点,振幅为零,这些点始终静止 不动,称为波节; 满足cos(2mx/,)=1的点,振幅最大,这些点的振 动最强,称为波腹。 波节的位置 2x克±k+0呀 x=+), k=0,1,2, 相邻两波节间的距离为 Xk+1一Xk= 2 波腹的位置 c0s2七 =1 X二士kπ x=土k k=0,1,2,… 相邻两波腹间的距离为 Xk+1一Xk=
•波节的位置 2、 波节和波腹 满足cos(2πx/λ)的点,振幅为零,这些点始终静止 不动,称为波节; 满足|cos(2πx/λ) |=1的点,振幅最大,这些点的振 动最强,称为波腹。 •概念 cos 2 =0 x ( ) 2 2 2 1 = k+ x ( ) , 0,1,2, 4 x = 2k 1 k = + 相邻两波节间的距离为 2 1 xk+ − xk = •波腹的位置 cos 2 =1 x k x 2 = , 0,1,2, 2 x = k k = 相邻两波腹间的距离为 2 1 xk+ − xk =

3、驻波的相位 y=2Ac0s2π片c0s2πt 使c0s(2x/)为正的点,相位为2πvt; 使c0s(2x/)为负的点,相位为2πvt+π。 在波节两侧点的振动相位相反。两个波节之间的点其振 动相位相同
3、 驻波的相位 t x y A = 2 cos2 cos2 使cos(2πx/λ)为正的点,相位为2πνt; 使cos(2πx/λ)为负的点,相位为2πνt+π。 * 在波节两侧点的振动相位相反。两个波节之间的点其振 动相位相同
三、相位跃变 有半波损失 1、实验现象 在支点处反射,形成波节;在自由 端反射,形成波腹。 2、波疏介质与波密介质 波阻:介质的密度和波速的乘积称为波阻。 波阻较大的介质称为波密介质; 波阻较小的介质称为波疏介质。 N 无半波损失 3、相位跃变与半波损失 在两种介质的分界面处形成波节,则反射波在分界 面上相位较之入射波跃变了π。相对于出现了半个波 长的波程差。把这种现象称为相位跃变或半波损 失
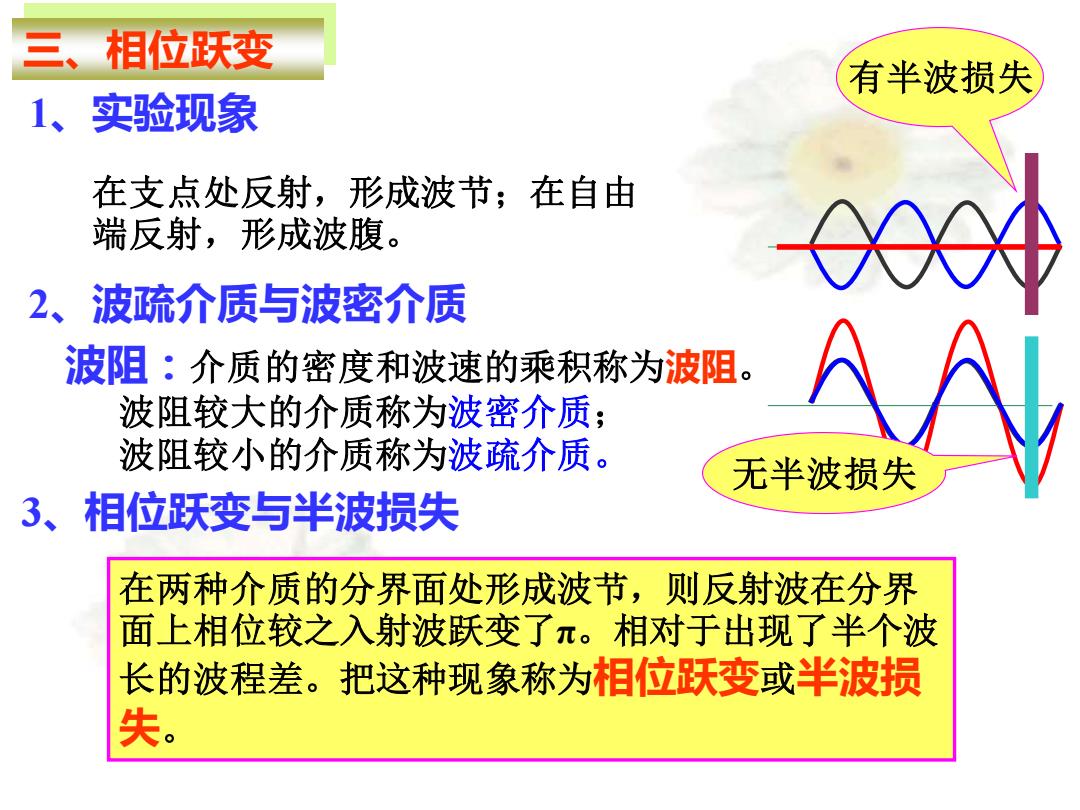
三、相位跃变 波阻:介质的密度和波速的乘积称为波阻。 波阻较大的介质称为波密介质; 波阻较小的介质称为波疏介质。 有半波损失 无半波损失 1、实验现象 在支点处反射,形成波节;在自由 端反射,形成波腹。 2、波疏介质与波密介质 3、相位跃变与半波损失 在两种介质的分界面处形成波节,则反射波在分界 面上相位较之入射波跃变了π。相对于出现了半个波 长的波程差。把这种现象称为相位跃变或半波损 失

四、驻波的能量 各质点位移达到最大时,动能为零,势能不为零。在波 节处相对形变最大,势能最大;在波腹处相对形变最小, 势能最小。势能集中在波节。 当各质点回到平衡位置时,全部势能为零;动能最大。 动能集中在波腹。 能量从波腹传到波节,又从波节传到波腹,往复循环, 能量不被传播
各质点位移达到最大时,动能为零,势能不为零。在波 节处相对形变最大,势能最大;在波腹处相对形变最小, 势能最小。势能集中在波节。 当各质点回到平衡位置时,全部势能为零;动能最大。 动能集中在波腹。 能量从波腹传到波节,又从波节传到波腹,往复循环, 能量不被传播。 四、驻波的能量

五、振动的简正模式 Fundamental 入=2L 在绳长为1的绳上形成驻波的波长必须满足下列条件 I=n 2 n=1,2,… 21 n=1,2,… (6) n W (c) 3 V= 2 n=1,2… 说明 弦线上形成的驻波波长、频率均不连 •系统究竟按那种模式振动, 续。 取决于初始条件。 这些频率称为弦振动的本征频率, 对应的振动方式称为简正模式。 •两端固定的弦,当距一端 某点受击而振动时,该点为 最低的频率称为基频, 波节的那些模式就不出现, 其它整倍数频率为谐频。 使演奏的音色更优美
, 1,2,... 2 = n = l u n n , 1,2,... 2 = n = n l n , 1,2,... 2 l = n n = n 在绳长为 l 的绳上形成驻波的波长必须满足下列条件: 五、振动的简正模式 弦线上形成的驻波波长、频率均不连 续。 这些频率称为弦振动的本征频率, 对应的振动方式称为简正模式。 最低的频率称为基频, 其它整倍数频率为谐频。 •两端固定的弦,当距一端 某点受击而振动时,该点为 波节的那些模式就不出现, 使演奏的音色更优美。 •系统究竟按那种模式振动, 取决于初始条件。 说明

例:如图所示,有一平面简谐波 A射液 y,=As27-克 P 反射波 向右传播,在距坐标原点O为=5的B 点被垂直界面反射,设反射处有半波 损失,反射波的振幅近似等于入射波 振幅。试求: (①)反射波的表达式; (2)驻波的表达式; (3)在原点O到反射点B之间各个波节 和波腹的坐标。 解:(1)首先要写出反射波在B的振动方程。依照题意,入 射波在B点的振动方程为 t yB=A0s2π(7-元》
例:如图所示,有一平面简谐波 cos 2 ( ) x T t yA = A − 向右传播,在距坐标原点O为l=5λ的B 点被垂直界面反射,设反射处有半波 损失,反射波的振幅近似等于入射波 振幅。试求: (1)反射波的表达式; (2)驻波的表达式; (3)在原点O到反射点B之间各个波节 和波腹的坐标。 解:(1) 首先要写出反射波在B的振动方程。依照题意,入 射波在B点的振动方程为 cos2 ( ) l T t y 入B = A −