
海大理学院放学裸件 大学物理学电子教案 简谐运动的应用 14-6简谐运动的合成 14-7阻尼振动、受迫振动、共振
大学物理学电子教案 海大理学院教学课件 简谐运动的应用 14-6 简谐运动的合成 14-7 阻尼振动、受迫振动、共振

复习 单摆和复摆 简谐运动的能量 E=m'o-
复习 单摆和复摆 简谐运动的能量 2 2 2 2 1 2 1 E= mA = kA

14-6简谐运动的合成 两个同方向同频率简谐运动的合成 某质点同时参与两个同频率且在同一条直线上的简谐运动 七1=Ac0s(ot+p,) Asino=A sing+A2 sinp2 x2 A2 cos(@t+o2) Acoso=A coso+42 cos2 合振动 x=x+x x=Acosocos@t-Asinosin@t =Acos(@t+o) 1、应用解析法 x=x+x2 A=+2+244 cos(2-) =A cos(@t+o:HA cos(@t+oz) =(A coso:+A2 cosp2)cos@t g0= A sinp+A2 sinpz -(A sing+A,sing,)sin@t A coso+4 cos
14-6 简谐运动的合成 一、两个同方向同频率简谐运动的合成 某质点同时参与两个同频率且在同一条直线上的简谐运动 ( ) ( ) 2 2 2 1 1 1 cos cos = + = + x A t x A t 合振动 x = x1 + x2 1、应用解析法 ( ) ( ) ( ) (A A ) t A A t A t A t x x x sin sin sin cos cos cos cos cos 1 1 2 2 1 1 2 2 1 1 2 2 1 2 − + = + + + = + = + 1 1 2 2 1 1 2 2 cos cos cos sin sin sin A A A A A A = + = + ( ) + − A t x A t A t cos cos cos sin sin = = 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − 1 1 2 2 1 1 2 2 cos cos sin sin A A A A tg + + = 令
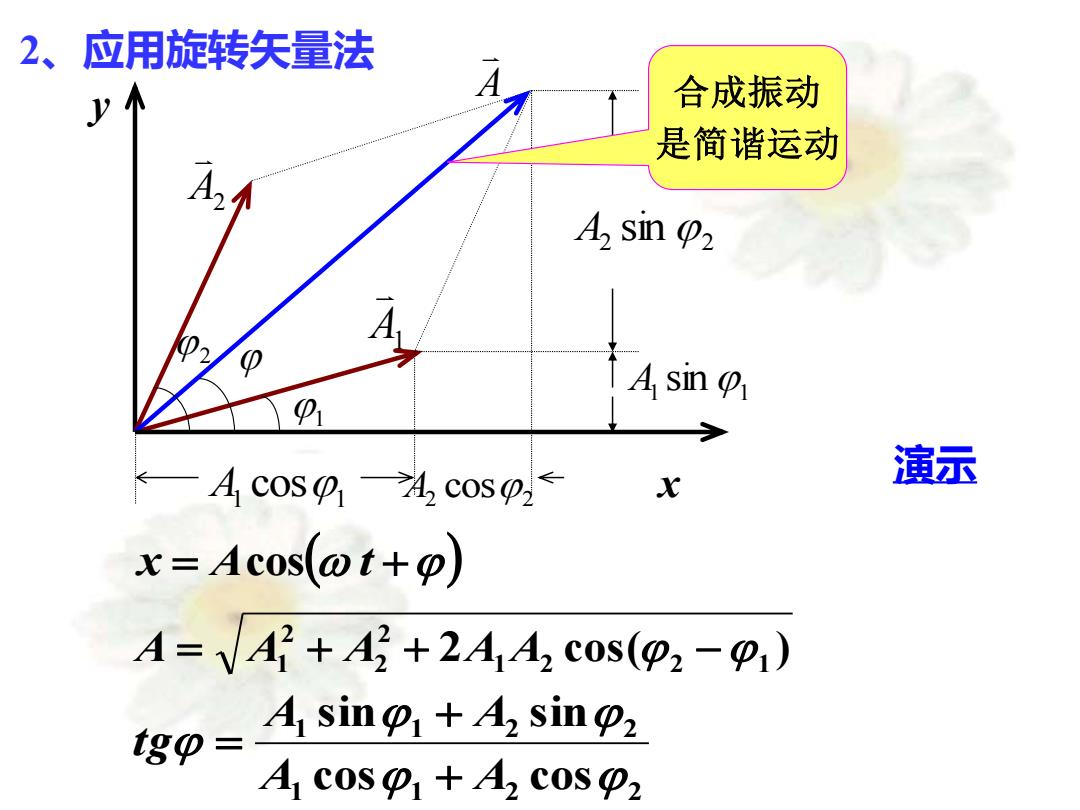
2、应用旋转矢量法 合成振动 是简谐运动 A sin p2 D A sin AC0Sp1A2c0sp≤ X 演示 x=Acos(@t+o) A=A2+A2+2442 cos(o2-g) A sin+42 sin t8⑩= A coso+42 cosp2
2、应用旋转矢量法 A2 A A1 2 1 x y 1 1 A cos 2 2 A cos 1 1 A sin 2 2 A sin 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − 1 1 2 2 1 1 2 2 cos cos sin sin A A A A t g + + = 合成振动 是简谐运动 x = Acos( t +) 演示

3、讨论 情况1 P2-P1=±2kπ k=0,1,2,… A=A1十A2 合振幅最大 当A1=A称为干涉相长A=2A 情况2 92-91=±(2k-1)π k=1,2,3, A A=A1一A2合振幅最小 当A1=A,称为干涉相消A=0 情况3:一般情况 P2-91≠kπ A21 4-4kA<4+44
3、讨论 2 −1 = 2k k = 0,1,2, A= A1 + A2 合振幅最大 A2 A A1 情况1 当 A1 = A2 称为干涉相长 A= 2A1 A2 A A1 A1 A2 A | | | | A1 − A2 A A1 + A2 2 −1 k 情况2 2 −1 = (2k −1) k = 1,2,3, A = A1 − A2 合振幅最小 当 A1 = A2 称为干涉相消 A= 0 情况3:一般情况

多个同方向同频率简谐运动的合成 振幅相等,初相位依次差一个恒量 x(t)=A cos@t 合振动是简谐运动 x,(t)=A,c0s(ot+△p) x3(t)=A3c0s(ot+2△p) 0A1 x(t)=AN cos[@t+(N-1)Ao] sin(NΔp/2) A=A0 A=2Rsin(N△p/2) sin(△gp/2) A=2Rsin(△p/2) ⑩= N-1A0 2 x(t)=Acos(@t+)=Ao sin(NA/2) W-1 cos(@t+- sin(△o/2) 2 △0)
二、多个同方向同频率简谐运动的合成 振幅相等,初相位依次差一个恒量 ( ) cos[ ( 1) ] ( ) cos( 2 ) ( ) cos( ) ( ) cos 3 3 2 2 1 1 = + − = + = + = x t A t N x t A t x t A t x t A t N N A1 A2 A3 A O x Q P 合振动是简谐运动 A = 2Rsin(N / 2) 2 sin( / 2) A0 = R sin( / 2) sin( / 2) 0 = N A A − = 2 N 1 ) 2 1 cos( sin( / 2) sin( / 2) 0 − + = N t N x(t) = Acos(t +) A

三、同方向不同频率的简谐振动的合成 质点同时参与两个不同频率且在同一条直线上的简谐振动 X1=A1c0s(@t+p1) X2=A2c0s(02t+p2) 合振动 x=x+x2 假设 A1=A2=A,91=p2=0 y1+V2>y1-V2 x1=A cos@t=A cos 2xvt A x2=42 cos@2t-Ao cos 27vt
三、同方向不同频率的简谐振动的合成 质点同时参与两个不同频率且在同一条直线上的简谐振动 ( ) ( ) 2 2 2 2 1 1 1 1 cos cos = + = + x A t x A t 合振动 x = x1 + x2 假设 A1 = A2 = A0 ,1 = 2 = 0 1 + 2 1 − 2 x A t A t x A t A t 2 2 2 0 2 1 1 1 0 1 cos cos 2 cos cos 2 = = = = 1 o x A1 A2 A 2
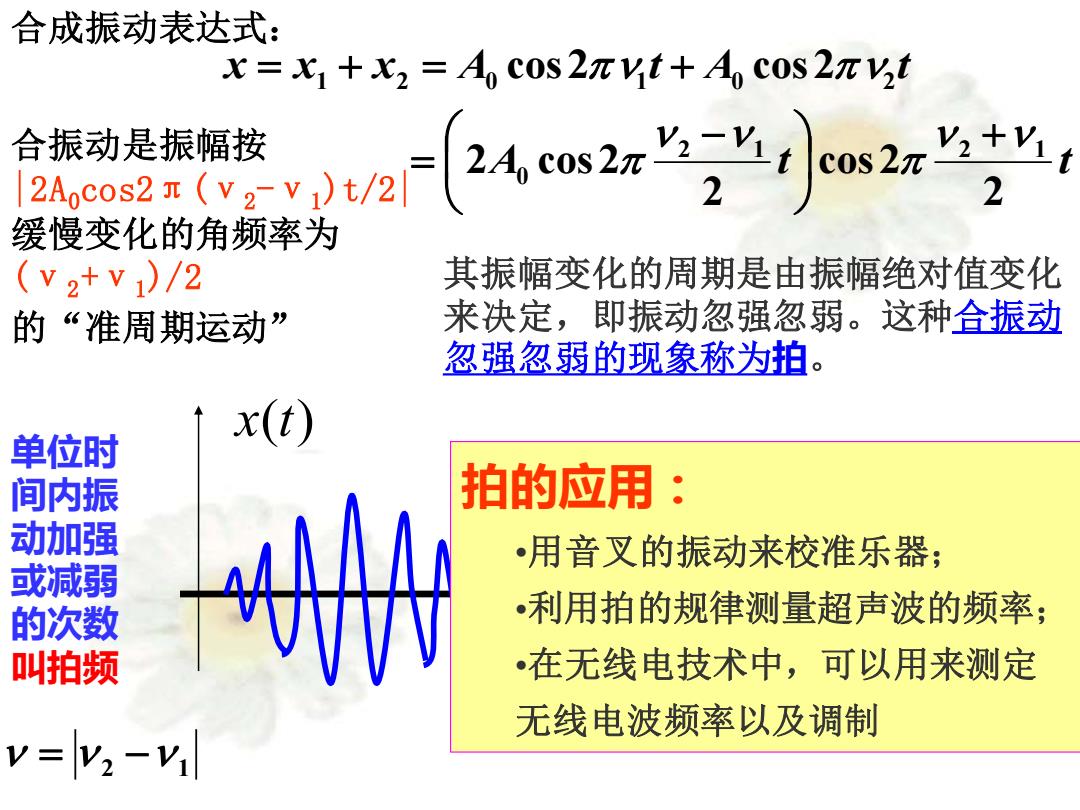
合成振动表达式: x=x+x2=Ao cos2xvt+Ao cos 27vt 高载动经货z(24o2r2'小s2e上” 合振动是振幅按 缓慢变化的角频率为 (v2+v)/2 其振幅变化的周期是由振幅绝对值变化 的“准周期运动” 来决定,即振动忽强忽弱。这种合振动 忽强忽弱的现象称为拍。 x(t) 单位时 间内振 拍的应用: 动加强 AA •用音叉的振动来校准乐器; 或减弱 的次数 •利用拍的规律测量超声波的频率; 叫拍频 在无线电技术中,可以用来测定 无线电波频率以及调制 v=v2-v
合成振动表达式: 其振幅变化的周期是由振幅绝对值变化 来决定,即振动忽强忽弱。这种合振动 忽强忽弱的现象称为拍。 A t t x x x A t A t 2 cos 2 2 2 cos 2 cos 2 cos 2 2 1 2 1 0 1 2 0 1 0 2 + − = = + = + 合振动是振幅按 |2A0cos2π(ν2-ν1)t/2| 缓慢变化的角频率为 (ν2+ν1)/2 的“准周期运动” 单位时 间内振 动加强 或减弱 的次数 叫拍频 x(t) t = 2 − 1 拍的应用: •用音叉的振动来校准乐器; •利用拍的规律测量超声波的频率; •在无线电技术中,可以用来测定 无线电波频率以及调制

四、两个相互垂直的同频率简谐振动的合成 某质点同时参与两个同频率的互相垂直方向的简谐运动 x=4 cos(@t+) y=A cos(@t+) 合振动的轨迹方程为 ,y2 2 cosp,-p,)=sin2(o,-g,) 是个椭圆方程,具体形状由相位差决定
四、两个相互垂直的同频率简谐振动的合成 某质点同时参与两个同频率的互相垂直方向的简谐运动 cos( ) = 1 +1 x A t cos( ) = 2 +2 y A t 合振动的轨迹方程为 ( ) ( ) 2 1 2 2 1 1 2 2 2 2 2 1 2 cos sin 2 + − − = − A A xy A y A x 是个椭圆方程,具体形状由相位差决定

讨论1 △p=p2-p1=0 2xy A =0 y= An x 合振动的轨迹是一条通过原点的直线 讨论2 △p=P2-p1=元 t? 2Xy=0 A 合振动的轨迹是一条通过原点的直线 讨论3 △p=p2-91=π/2 =1 合振动的轨迹是的椭圆 方程,且顺时针旋转
讨论1 =2 −1 = 0 0 2 1 2 2 2 2 2 1 2 + − = A A xy A y A x x A A y 1 2 = 合振动的轨迹是一条通过原点的直线 y x 讨论2 0 2 1 2 2 2 2 2 1 2 + + = A A xy A y A x x A A y 1 2 = − y x =2 −1 = 合振动的轨迹是一条通过原点的直线 讨论3 1 2 2 2 2 1 2 + = A y A x =2 −1 = / 2 合振动的轨迹是的椭圆 方程,且顺时针旋转