
海大理学院教学保件 大学物理学电子教案 气体动理论(3) 7-7分子平均碰撞次数和平均自由程 7-8气体的迁移现象 7-9实际气体的范德瓦耳斯方程 7-10热力学第二定律的统计意义
大学物理学电子教案 海大理学院教学课件 气体动理论(3) 7-7 分子平均碰撞次数和平均自由程 7-8 气体的迁移现象 7-9 实际气体的范德瓦耳斯方程 7-10 热力学第二定律的统计意义

复习 •自由度 ·能量均分定理 理想气体的内能和摩尔热容 •速率分布函数的物理意义 •麦克斯韦速率分布律 ·三种统计速率 •玻尔兹曼能量分布律 ·重力场中等温气压公式
复 习 •自由度 •能量均分定理 •理想气体的内能和摩尔热容 •速率分布函数的物理意义 •麦克斯韦速率分布律 •三种统计速率 •玻尔兹曼能量分布律 •重力场中等温气压公式

7-7分子平均碰撞次数和平均自由程 分子碰撞的引入: 分子热运动速率很大,平均速 率可达几百米/秒,而扩散运动 却进行得很慢。 克劳修斯为了说明这个问题,提出了分子碰撞次数与自由 程的概念。 分子碰撞的概念不仅解决了上述问题,气体动理论在 更加坚实的基础上向前推动了一步。 研究碰撞的意义: 分子间通过碰撞,实现动量与动能的交换; 分子间通过碰撞交换能量达到能量按自由度均分; 分子间通过碰撞,由非平衡状态向平衡状态过渡: 分子间通过碰撞交换速度,使速度分布达到稳定
7-7 分子平均碰撞次数和平均自由程 分子碰撞的引入: 分子热运动速率很大,平均速 率可达几百米/秒,而扩散运动 却进行得很慢。 克劳修斯为了说明这个问题,提出了分子碰撞次数与自由 程的概念。 分子碰撞的概念不仅解决了上述问题,气体动理论在 更加坚实的基础上向前推动了一步。 研究碰撞的意义: 分子间通过碰撞,实现动量与动能的交换; 分子间通过碰撞交换能量达到能量按自由度均分; 分子间通过碰撞,由非平衡状态向平衡状态过渡; 分子间通过碰撞交换速度,使速度分布达到稳定

平均自由程和平均碰撞次数的定义 1、平均自由程入 分子两次相邻碰撞之间自由通过的路程, 叫做自由程;分子在连续两次碰撞之间 所经过的路程的平均值叫做平均自由程。 2、平均碰撞频率7 在单位时间内一个分子与其它分子碰撞的平均次数,叫 做分子的平均碰撞次数或平均碰撞频率。 3、二者关系
一、平均自由程 和平均碰撞次数的定义 Z v = 2、平均碰撞频率 Z 在单位时间内一个分子与其它分子碰撞的平均次数,叫 做分子的平均碰撞次数或平均碰撞频率。 3、二者关系 1、平均自由程 分子两次相邻碰撞之间自由通过的路程, 叫做自由程;分子在连续两次碰撞之间 所经过的路程的平均值叫做平均自由程

二、 平均自由程和平均碰撞次数的计算 分子碰撞模型 (1)分子可看作具有一定体积的刚球; (2)分子间的碰撞是弹性碰撞; (3)两个分子质心间最小距离的平均值认为 是刚球的直径,称为分子的有效直径,用d表 示。 2、平均碰撞次数 假设只有一个分子以平均 速度运动,其余分子看成 不动。分子A的运动轨迹为 一折线,以A的中心运动轨 迹为轴线,以分子有效直 a 径d为半径,作一曲折圆 柱体。凡中心在此圆柱体 内的分子都会与A相碰
假设只有一个分子以平均 速度运动,其余分子看成 不动。分子A的运动轨迹为 一折线,以A的中心运动轨 迹为轴线,以分子有效直 径d 为半径,作一曲折圆 柱体。凡中心在此圆柱体 内的分子都会与A相碰。 二、平均自由程和平均碰撞次数的计算 1、分子碰撞模型 (1)分子可看作具有一定体积的刚球; (2)分子间的碰撞是弹性碰撞; (3)两个分子质心间最小距离的平均值认为 是刚球的直径,称为分子的有效直径,用d 表 示。 2、平均碰撞次数 d A

圆柱体的截面积为σ= 元d2,叫做分子的碰 撞截面。 在△t内,A所走过的路程 为△t,相应圆柱体的 体积为ov△t,设气体 分子数密度为n。则 中心在此圆柱体内的分子 总数,亦即在△t时间 修正:对于实际气体,各个分子 内与A相碰的分子数为 都在运动,且运动速率服从麦克 nov△t 斯韦分布率,对上式加以修正后, 得 平均碰撞次数 no y Z=√2ovn=√2πd2n △t
在t内,A所走过的路程 为 ,相应圆柱体的 体积为 ,设气体 分子数密度为n。则 中心在此圆柱体内的分子 总数,亦即在t时间 内与A相碰的分子数为 vt vt n vt n v t n v t Z = = Z vn d vn 2 = 2 = 2 圆柱体的截面积为 = d 2 ,叫做分子的碰 撞截面。 平均碰撞次数 修正:对于实际气体,各个分子 都在运动,且运动速率服从麦克 斯韦分布率,对上式加以修正后, 得 d A
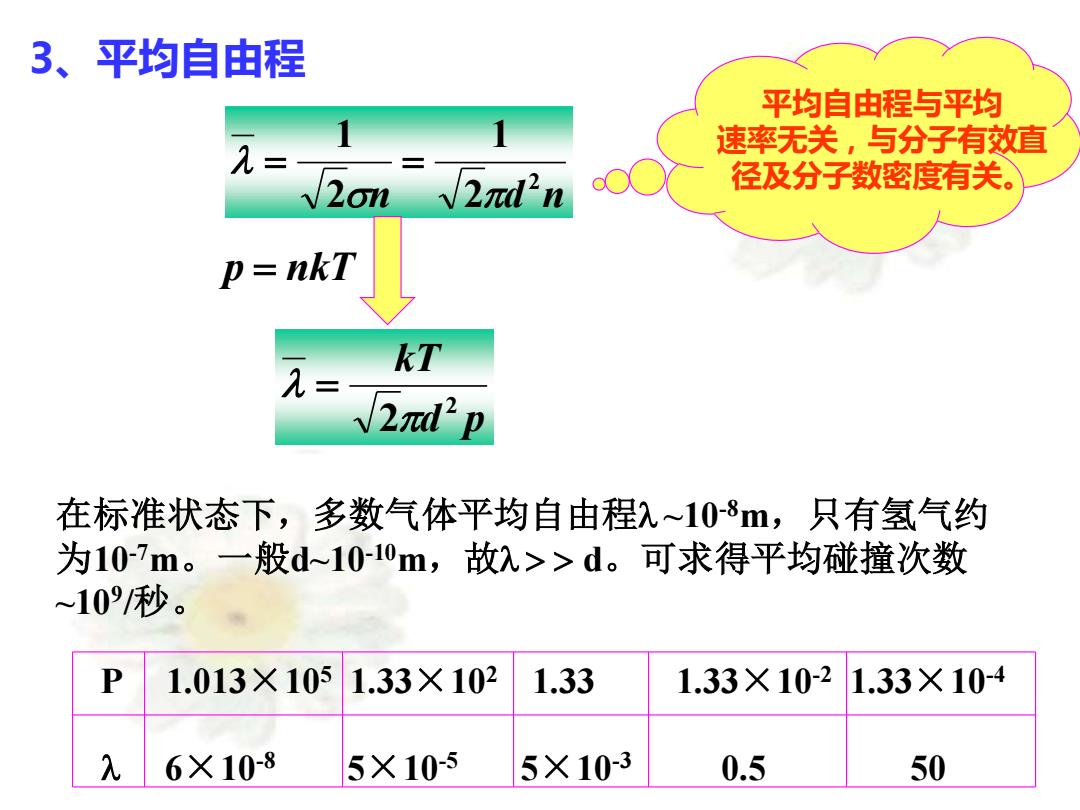
3、平均自由程 平均自由程与平均 速率无关,与分子有效直 √2omV2πd'n 径及分子数密度有关。 p=nkT kT √2π'p 在标准状态下,多数气体平均自由程入~10-8,只有氢气约 为10m。一般d~10-0m,故入>>d。可求得平均碰撞次数 ~10/秒。 P 1.013×1051.33×102 1.33 1.33×10-2 1.33×10-4 6X10-8 5×105 5×10-3 0.5 50
3、平均自由程 n d n 2 2 1 2 1 = = d p kT 2 2 = p = nkT 在标准状态下,多数气体平均自由程 ~10-8m,只有氢气约 为10-7m。一般d~10-10m,故 d。可求得平均碰撞次数 ~109 /秒。 平均自由程与平均 速率无关,与分子有效直 径及分子数密度有关。 P 1.013×105 1.33×102 1.33 1.33×10-2 1.33×10-4 6×10-8 5×10-5 5×10-3 0.5 50

7-8气体的迁移现象 当气体处于非平衡状态下,气体内部或者各部分的温度不 相等,或者各部分的压强不相等,或者各气层之间有相对 运动,或者这三者同时存在。在这些非平衡状态下,气体 内部将有能量、质量或动量从一个部分向另一个部分定向 迁移,这就是在非平衡状态下气体的迁移现象。 热传导现象一由于气体内部温度不同而产生的能量的 迁移现象 扩散现象 一由于气体内部分子数密度不同而产生的 质量的迁移现象 粘滞现象一! 由于气体内部各气层流速不同而产生的动 量的迁移现象
当气体处于非平衡状态下,气体内部或者各部分的温度不 相等,或者各部分的压强不相等,或者各气层之间有相对 运动,或者这三者同时存在。在这些非平衡状态下,气体 内部将有能量、质量或动量从一个部分向另一个部分定向 迁移,这就是在非平衡状态下气体的迁移现象。 热传导现象——由于气体内部温度不同而产生的能量的 迁移现象 扩散现象 ——由于气体内部分子数密度不同而产生的 质量的迁移现象 粘滞现象——由于气体内部各气层流速不同而产生的动 量的迁移现象 7-8 气体的迁移现象
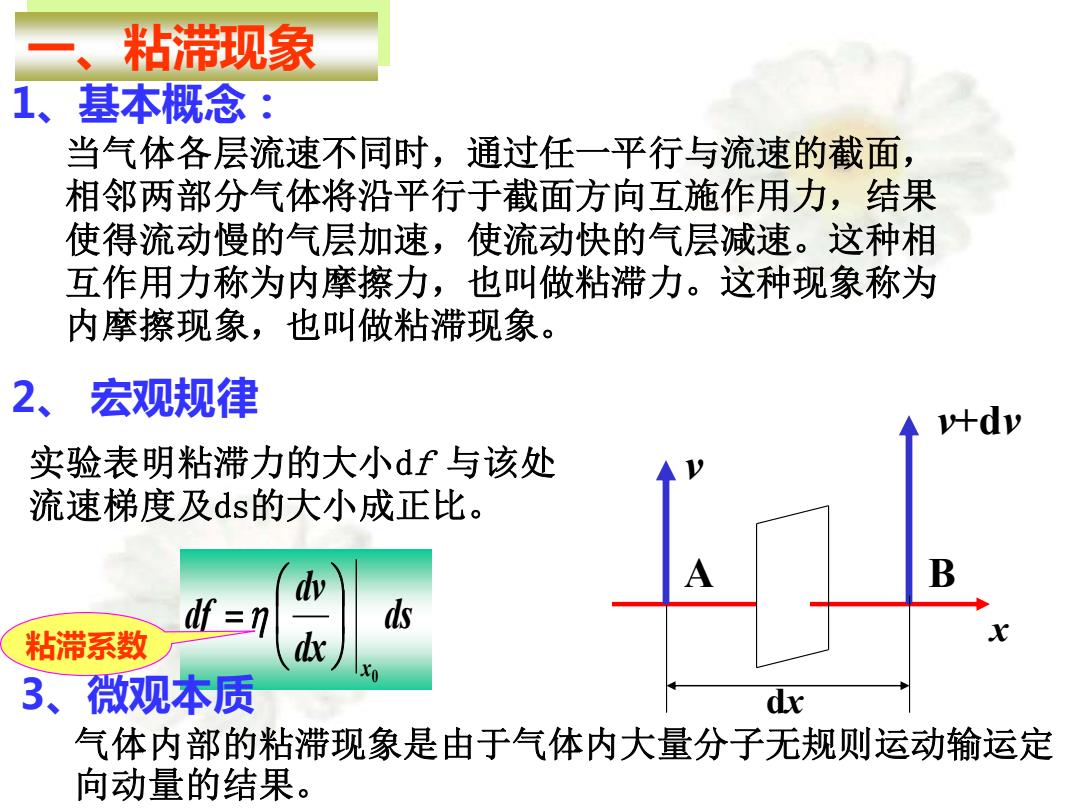
、} 粘滞现象 1、基本概念: 当气体各层流速不同时,通过任一平行与流速的截面, 相邻两部分气体将沿平行于截面方向互施作用力,结果 使得流动慢的气层加速,使流动快的气层减速。这种相 互作用力称为内摩擦力,也叫做粘滞力。这种现象称为 内摩擦现象,也叫做粘滞现象。 2、宏观规律 v+dv 实验表明粘滞力的大小df与该处 流速梯度及ds的大小成正比。 df =n ds 粘滞系数 3、微观本质 dx 气体内部的粘滞现象是由于气体内大量分子无规则运动输运定 向动量的结果
2、 宏观规律 1、基本概念: 当气体各层流速不同时,通过任一平行与流速的截面, 相邻两部分气体将沿平行于截面方向互施作用力,结果 使得流动慢的气层加速,使流动快的气层减速。这种相 互作用力称为内摩擦力,也叫做粘滞力。这种现象称为 内摩擦现象,也叫做粘滞现象。 一、粘滞现象 A B x dx v v+dv 实验表明粘滞力的大小df 与该处 流速梯度及ds的大小成正比。 0 ds dx dv df x = 粘滞系数 3、微观本质 气体内部的粘滞现象是由于气体内大量分子无规则运动输运定 向动量的结果
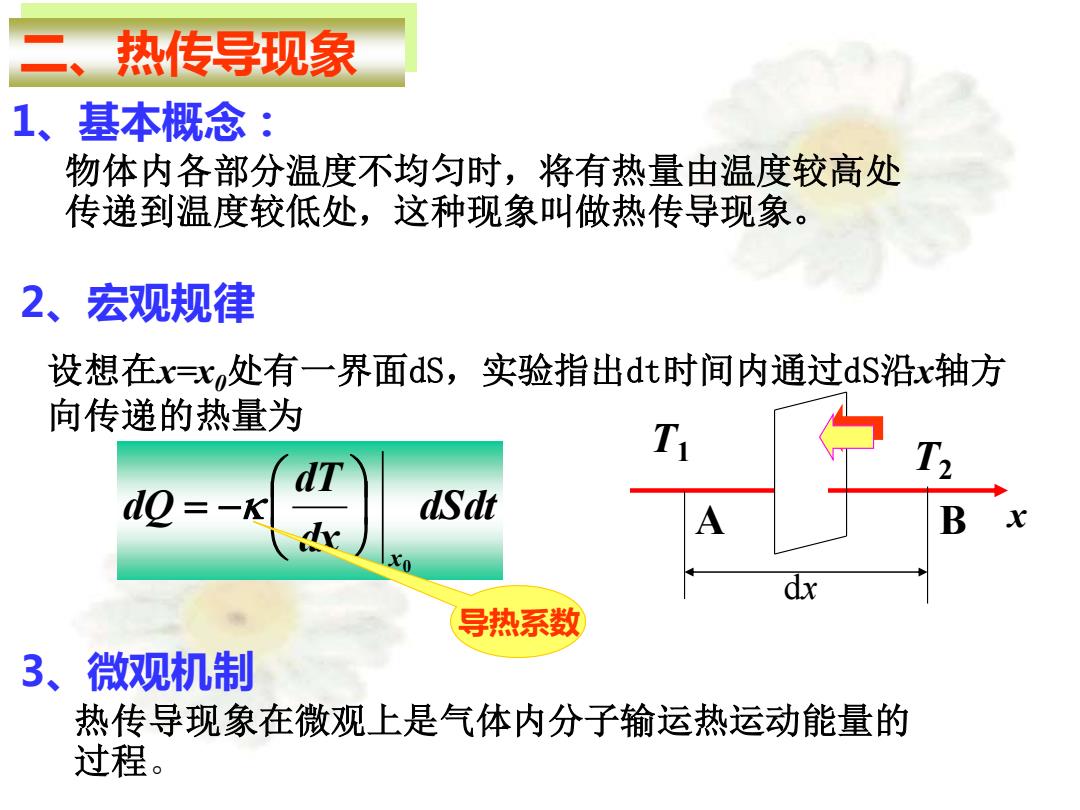
热传导现象 1、基本概念: 物体内各部分温度不均匀时,将有热量由温度较高处 传递到温度较低处,这种现象叫做热传导现象。 2、宏观规律 设想在x=X处有一界面dS,实验指出dt时间内通过dS沿x轴方 向传递的热量为 T do=-K dSdt B 导热系数 3、微观机制 热传导现象在微观上是气体内分子输运热运动能量的 过程
2、宏观规律 1、基本概念: 物体内各部分温度不均匀时,将有热量由温度较高处 传递到温度较低处,这种现象叫做热传导现象。 二、热传导现象 A B x dx T1 T2 3、微观机制 热传导现象在微观上是气体内分子输运热运动能量的 过程。 设想在x=x0处有一界面dS,实验指出dt时间内通过dS沿x轴方 向传递的热量为 dSdt dx dT dQ x0 = − 导热系数