
海大理学院放学保件 大学物理学电子教案 质点运动学一应用 1-2加速度为恒矢量时的质点运动 1-3圆周运动 1-4相对运动
1-2 加速度为恒矢量时的质点运动 1-3 圆周运动 1-4 相对运动 大学物理学电子教案 海大l理学院教学课件 质点运动学——应用

复习 三个概念: 1.参考系 为描述物体的运动而选择的标准物 2.坐标系 定量确定物体相对于参考系的位置 3.质点 把物体当做只有质量没有形状和大小的 点 描述质点运动的四个物理量: 1、位置矢量 产xi十yj+zk 4、加速度 2、位移 △r=g- d而 d标 3.速度 D= dt dt
复 习 三个概念: 1. 参考系——为描述物体的运动而选择的标准物 2. 坐标系——定量确定物体相对于参考系的位置 3. 质点 ——把物体当做只有质量没有形状和大小的 点 描述质点运动的四个物理量: 1、位置矢量 r xi yj zk = + + 2、位移 2 1 r r r = − 3.速度 dt dr v = 4、加速度 2 2 dt d r dt dv a = =

1-2加速度为恒矢量时的质点运动 加速度为恒矢量时的运动方程 问题:假设质点作曲线运动,其加速度为恒量 在0时,质点的ro,yo 求在任意时刻,质点的位置矢量、位移和速度。 1.速度 ∫w=小a ye=yxo十at y=y十at =v。十at v:=zo十a,t
1-2 加速度为恒矢量时的质点运动 一、加速度为恒矢量时的运动方程 问题:假设质点作曲线运动,其加速度a为恒量 在t=0时,质点的r0 ,v0, 求在任意时刻t,质点的位置矢量、位移和速度。 1.速度 = v t v dv adt 0 0 v v at = 0 + v v a t v v a t v v a t z z z y y y x x x = + = + = + 0 0 0

2.位移和位置矢量 d=dt=[。+at]h 产-月=t+ x-x-Yal+Tap ) x=,++20, 1 y-,=y0t+5a,2 1 2 y=o+vyot+ 2 1 Z-Zo=V:0t+ 02 1 2 Z=Zo+v:ot+at2 3、运动的叠加原理或运动的独立性原理 曲线可以运动分解为几个垂直方向的运动。 演示 ·当物体同时参与两个或多个运动时,其总的运 动乃是各个独立运动的合成结果
2.位移和位置矢量 dr vdt v atdt = = 0 + 2 0 0 2 1 r r v t at − = + 2 0 0 2 0 0 2 0 0 2 1 2 1 2 1 z z v t a t y y v t a t x x v t a t z z y y x x − = + − = + − = + 2 0 0 2 0 0 2 0 0 2 1 2 1 2 1 z z v t a t y y v t a t x x v t a t z z y y x x = + + = + + = + + 曲线可以运动分解为几个垂直方向的运动。 •当物体同时参与两个或多个运动时,其总的运 动乃是各个独立运动的合成结果。 3、运动的叠加原理或运动的独立性原理 演示
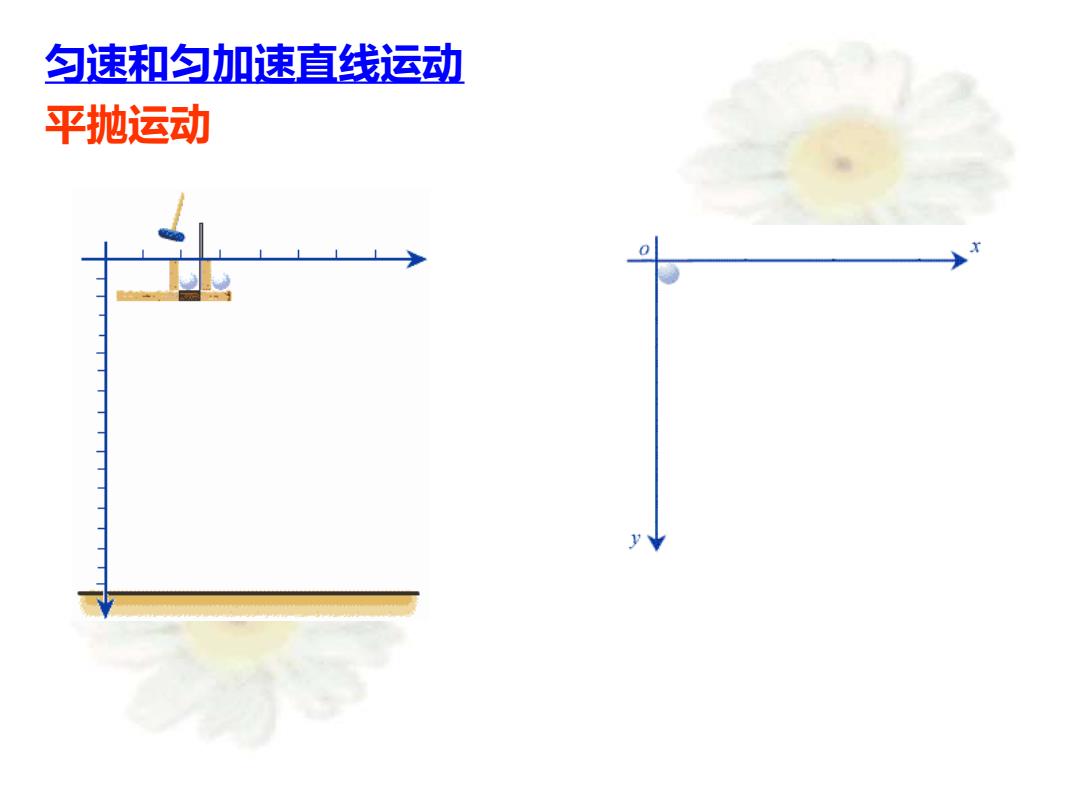
匀速和匀加速直线运动 平抛运动 0
匀速和匀加速直线运动 平抛运动
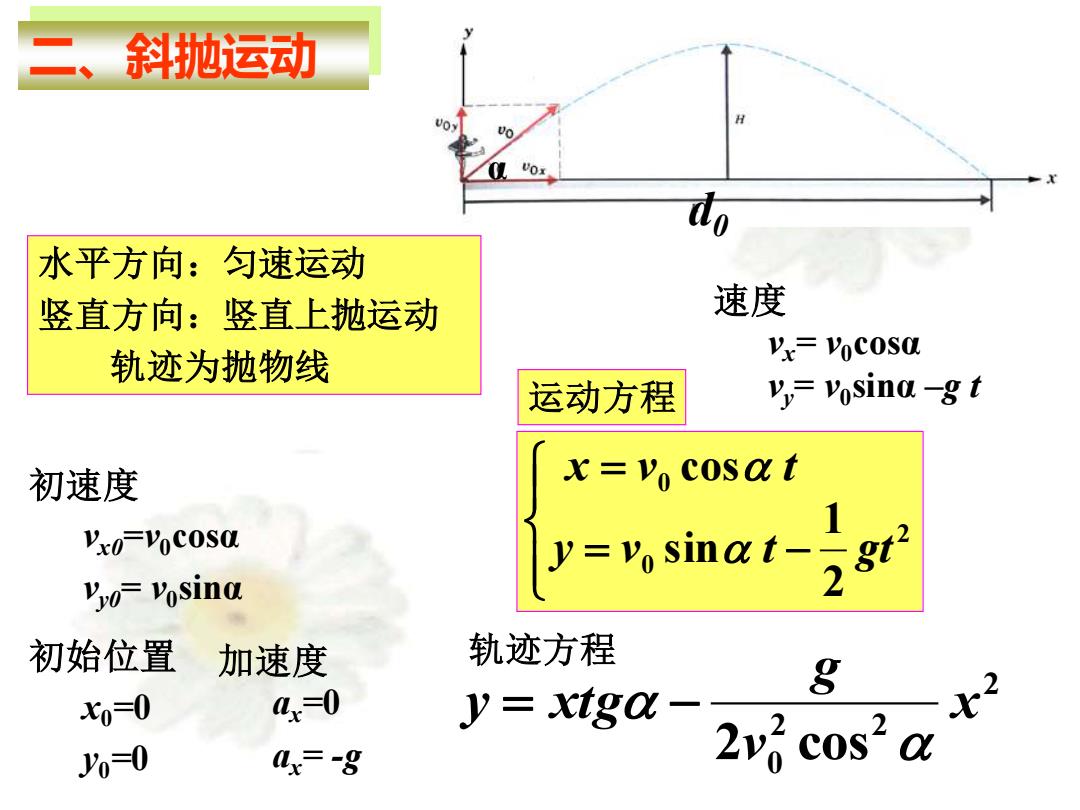
二、斜抛运动 水平方向:匀速运动 竖直方向:竖直上抛运动 速度 轨迹为抛物线 Vx=Vocosa 运动方程 vy=vosina-g t 初速度 x=vo cosa t Vxo=vocosa Yyo=vosina y-vsinat-7gt 初始位置 加速度 轨迹方程 g x0=0 4=0 Jy=xtg0一 %=0 Lx=-8 2v cos"a
二、斜抛运动 初速度 vx0=v0cosα vy0= v0 sinα 初始位置 x0=0 y0=0 加速度 ax =0 ax= -g 2 2 2 0 2 cos x v g y xtg = − 轨迹方程 = − = 2 0 0 2 1 sin cos y v t gt x v t 运动方程 水平方向:匀速运动 竖直方向:竖直上抛运动 轨迹为抛物线 d0 α 速度 vx= v0cosα vy= v0 sinα –g t

讨论 射程:抛体落地点与抛出点之间的距离 2y2 o sina cosa=o sin2a g 8 dd_.cos20 da g 20=π/2,0=元/4 70 dom 20
讨论 射程:抛体落地点与抛出点之间的距离 sin cos sin2 2 2 0 2 0 0 g v g v d = = cos 2 0 2 d d 2 0 0 = = g d v 2= / 2,= / 4 g v d m 2 0 0 =
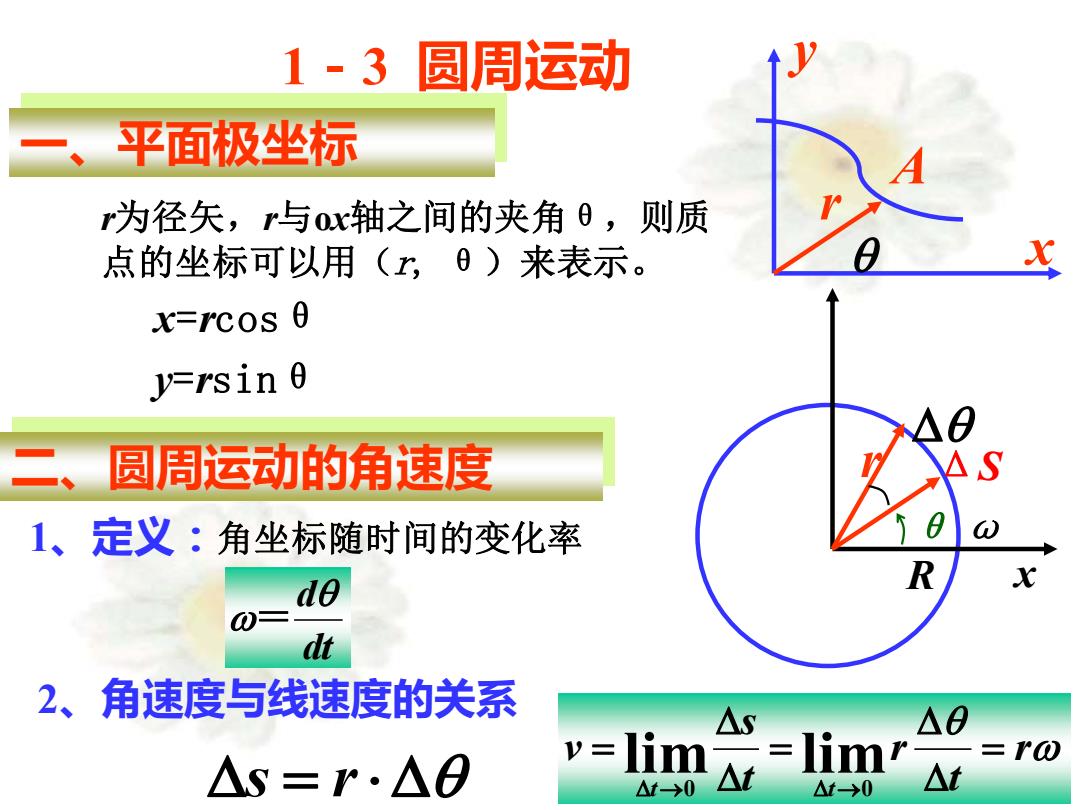
1·3圆周运动 平面极坐标 为径矢,与o轴之间的夹角0,则质 点的坐标可以用(,日)来表示。 X=r℃0S0 y=rsin 0 二 圆周运动的角速度 1、定义:角坐标随时间的变化率 do dt 2、角速度与线速度的关系 △s △ -=r0 △s=r.△0 V= =limr
1-3 圆周运动 一、平面极坐标 y r x A r为径矢,r与ox轴之间的夹角θ,则质 点的坐标可以用(r, θ)来表示。 x=rcosθ y=rsinθ 二、圆周运动的角速度 1、定义:角坐标随时间的变化率 dt d = 2、角速度与线速度的关系 s = r r t r t s v t t = = = → → lim 0 lim 0 r θ x ΔS ω R

三、圆周运动的角加速度 1、角加速度的定义 △0 a=lim△ do )d20 △t-→0 _dt dt2 2、切向加速度与法向加速度 立=ve a= d = dv dt dt e+ dt dy do 切向加速度 dt _dt e,=roe
三、圆周运动的角加速度 1、角加速度的定义 2 2 0 lim dt d dt d t t = = → = 2、切向加速度与法向加速度 t v ve = v dt de e dt dv v dt d a t t = = + t t t t e r e dt d e r dt dv a 切向加速度 = = =

法向加速度 de, dt dt n=v- =voe, t a=(a+)2 an" =r01 tgφ= a, 曲线运动 R为曲率半径
法向加速度 n n n e v e dt d a v = = n t e dt d dt de = 2 2 r r v an = = t n n t a a tg a a a = = + 2 2 1/ 2 ( ) r 曲线运动 R R为曲率半径