
第二章牛顿定律部分习题分析与解答 第典章分可翼分桥解答
第二章 牛顿定律部分习题分析与解答

第二章牛顿定律部分习题分析与解答 2-2假使地球自转速度加快到能使赤道上的物体处于 失重状态,一昼夜的时间有多长? 分新:由于物体地球自转时,有向心加速度存在当 提供此加速度的力即为重力时,物体处于失重 状态,由向心加速度和角速度的关系就可得一 昼夜所需的时间. 解倍:按题意有:mg=m7w2-mr(2不) 则地球自转一天所需的时间为: T=2πVr/g=2πV6.378×10619.8 =5.07×103s≈1.4h
第二章 牛顿定律部分习题分析与解答 2-2 假使地球自转速度加快到能使赤道上的物体处于 失重状态,一昼夜的时间有多长? 按题意有: 2 2 ) 2 ( T m g m r m r = = 由于物体地球自转时,有向心加速度存在.当 提供此加速度的力即为重力时,物体处于失重 状态,由向心加速度和角速度的关系就可得一 昼夜所需的时间. 则地球自转一天所需的时间为: s h T r g 5.07 10 1.4 2 / 2 6.378 10 / 9.8 3 6 = = =
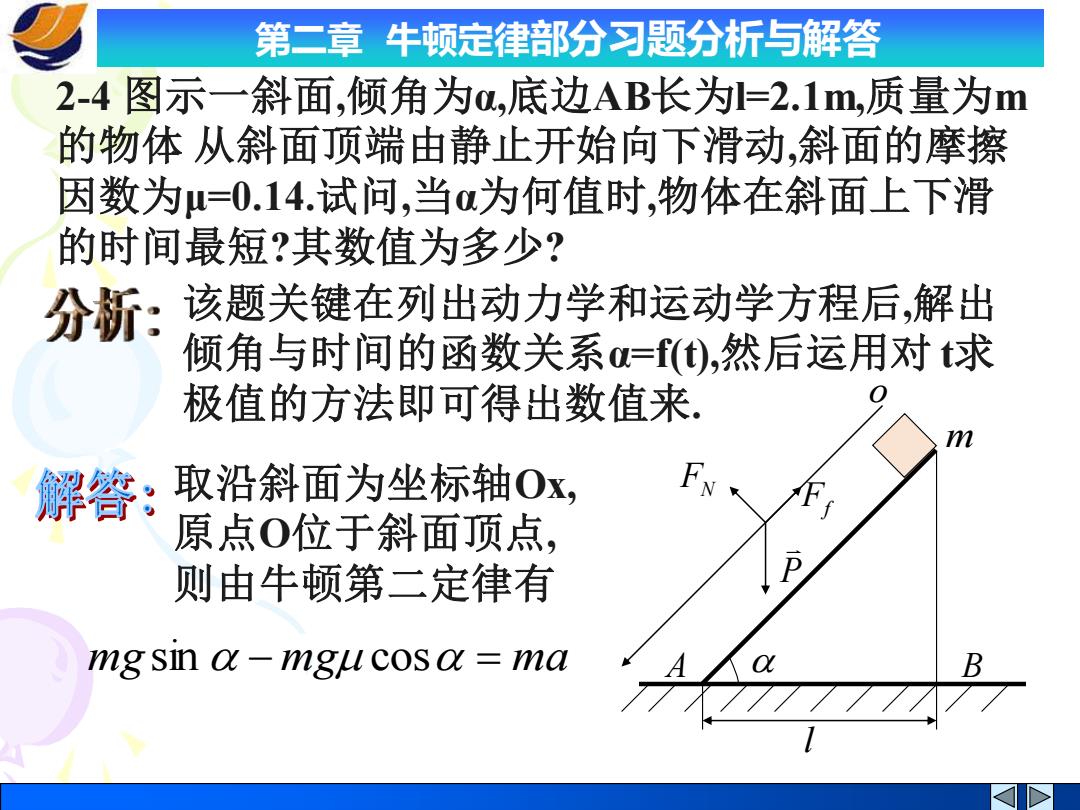
第二章牛顿定律部分习题分析与解答 2-4图示一斜面,倾角为o,底边AB长为=2.1m,质量为m 的物体从斜面顶端由静止开始向下滑动,斜面的摩擦 因数为=0.14.试问,当o为何值时,物体在斜面上下滑 的时间最短?其数值为多少? 分新:该题关键在列出动力学和运动学方程后,解出 倾角与时间的函数关系=(①),然后运用对求 极值的方法即可得出数值来。 0 解答: 取沿斜面为坐标轴Ox, 原点O位于斜面顶点, 则由牛顿第二定律有 mg sin a-mgu cosa ma
第二章 牛顿定律部分习题分析与解答 2-4 图示一斜面,倾角为α,底边AB长为l=2.1m,质量为m 的物体 从斜面顶端由静止开始向下滑动,斜面的摩擦 因数为μ=0.14.试问,当α为何值时,物体在斜面上下滑 的时间最短?其数值为多少? 取沿斜面为坐标轴Ox, 原点O位于斜面顶点, 则由牛顿第二定律有 mg sin − mg cos = ma 该题关键在列出动力学和运动学方程后,解出 倾角与时间的函数关系α=f(t),然后运用对 t求 极值的方法即可得出数值来. P Ff FN o m A B l

第二章牛顿定律部分习题分析与解答 又物体在斜面上作匀变速直线运动,故有: 1 1/cosa=-at =。8(sina-ucosa)t 2 21 则: t= g cosa(sin a-ucosa) 为使下滑时间最短,可令dt/da=O,由上式得: sin a(sin a-ucosa)+cosa(cosa+usin a)=0 则可得: tg20=-1/4, c=490 21 此时: =0.99s g cosa(sin a-ucosa)
第二章 牛顿定律部分习题分析与解答 又物体在斜面上作匀变速直线运动,故有: 2 2 (sin cos ) 2 1 2 1 l / cos = at = g − t 则: cos (sin cos ) 2 − = g l t 为使下滑时间最短,可令 dt / d = 0 ,由上式得: −sin (sin − cos) + cos(cos + sin ) = 0 则可得: 0 t g2 = −1/ , = 49 此时: s g l t 0.99 cos (sin cos ) 2 min = − =

第二章牛顿定律部分习题分析与解答 2-8直升飞机的螺旋桨由两个对称的叶片组成.每 一叶片的质量=136kg,长=3.66m,求当它的转速 n=320r/min时,两个叶片根部的张力.(设叶片是宽 度一定、厚度均匀的薄片) 分新:螺旋桨旋转时,叶片上各点的加速度不同,在 其各部分两侧的张力也不同;由于叶片的质量 是连续分布的,在求叶片根部的张力时,可选 取叶片上一小段,分析其受力,列出动力学方 程,然后采用积分的方法求解
第二章 牛顿定律部分习题分析与解答 2-8 直升飞机的螺旋桨由两个对称的叶片组成.每 一叶片的质量m=136kg,长l=3.66m,求当它的转速 n=320r/min时,两个叶片根部的张力.(设叶片是宽 度一定、厚度均匀的薄片) 螺旋桨旋转时,叶片上各点的加速度不同,在 其各部分两侧的张力也不同;由于叶片的质量 是连续分布的,在求叶片根部的张力时,可选 取叶片上一小段,分析其受力,列出动力学方 程,然后采用积分的方法求解
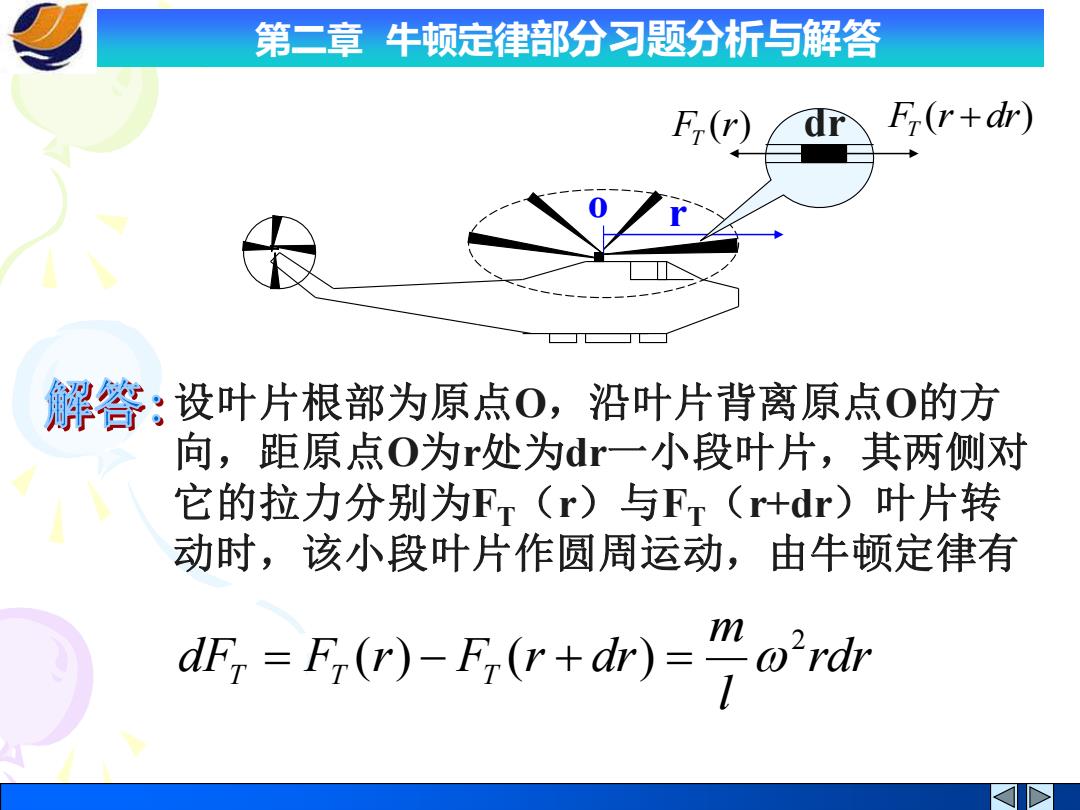
第二章牛顿定律部分习题分析与解答 F(r F(r+dr) 解答:设叶片根部为原点0,沿叶片背离原点0的方 向,距原点O为r处为d一小段叶片,其两侧对 它的拉力分别为FT(r)与FT(r+dr)叶片转 动时,该小段叶片作圆周运动,由牛顿定律有 dF,=F(r)-Fi(r+dr)-oindr
第二章 牛顿定律部分习题分析与解答 设叶片根部为原点O,沿叶片背离原点O的方 向,距原点O为r处为dr一小段叶片,其两侧对 它的拉力分别为FT(r)与FT(r+dr)叶片转 动时,该小段叶片作圆周运动,由牛顿定律有 o r F (r) dr T F (r dr) T + rdr l m dF F r F r dr T T T 2 = ( ) − ( + ) =

第二章牛顿定律部分习题分析与解答 由于r=1时外侧F=O所以有: mrdr F)=- m (2-2)=- 2π2mn (2-2 上式中取·=0,即得叶片根部的张力 F。=-2.79×105N 负号表示张力方向与坐标方向相反
第二章 牛顿定律部分习题分析与解答 由于 r = l 时外侧 = 0 ,所以有: FT = 0 ( ) 2 F r l r T T rdr l m dF ( ) 2 ( ) 2 ( ) 2 2 2 2 2 2 2 l r l m n l r l m F r T = − − = − − 上式中取 r = 0 ,即得叶片根部的张力 FTo N 5 = −2.7910 负号表示张力方向与坐标方向相反

第二章牛顿定律部分习题分析与解答 2-9在一只半径为R的半球形碗内,有一粒质量为m 的小钢球。当钢球以角速度。在水平面内沿碗内壁作 匀速圆周运动时,它距碗旅底有多高? 分新:维持钢球在水平面内作匀角速度转动时,必 须使钢球受到一与向心加速度相对应的力 (向心力),而该力是由碗内壁对球的支持 力FN的分力来提供的,由于支持为FN始终 垂直于碗内壁,所以支持力的大小和方向是 随o而变的。取图示Oxy坐标,列出动力学 方程,即可求解钢球距碗底的高度
第二章 牛顿定律部分习题分析与解答 2-9在一只半径为R的半球形碗内,有一粒质量为m 的小钢球。当钢球以角速度ω在水平面内沿碗内壁作 匀速圆周运动时,它距碗旅底有多高? 维持钢球在水平面内作匀角速度转动时,必 须使钢球受到一与向心加速度相对应的力 (向心力),而该力是由碗内壁对球的支持 力FN的分力来提供的,由于支持为FN始终 垂直于碗内壁,所以支持力的大小和方向是 随ω而变的。取图示Oxy坐标,列出动力学 方程,即可求解钢球距碗底的高度
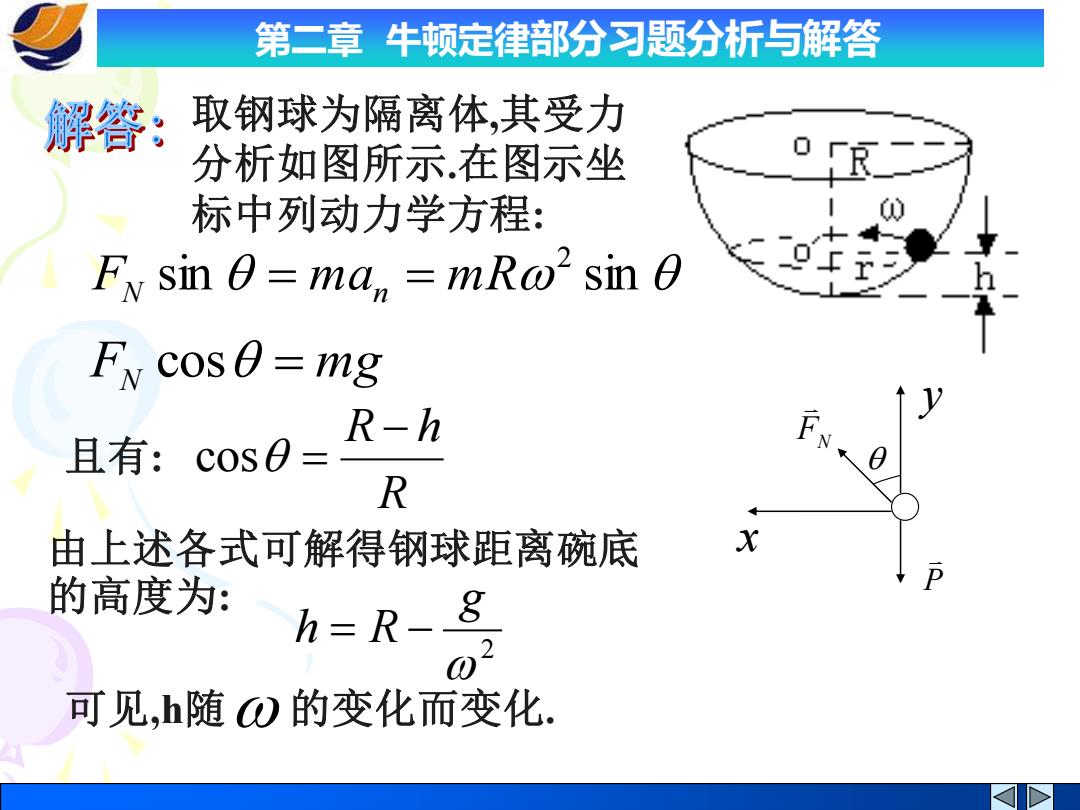
第二章牛顿定律部分习题分析与解答 解答: 取钢球为隔离体,其受力 分析如图所示在图示坐 标中列动力学方程: Fyv sin 0=ma mRo'sin 0 FN cos=mg 且有: COS0= R-h R 由上述各式可解得钢球距离碗底 的高度为: h=R、8 可见,h随0的变化而变化
第二章 牛顿定律部分习题分析与解答 P FN y x 取钢球为隔离体,其受力 分析如图所示.在图示坐 标中列动力学方程: sin sin 2 FN = m an = m R FN cos = mg 且有: R R − h cos = 由上述各式可解得钢球距离碗底 的高度为: 2 g h = R − 可见,h随 的变化而变化

第二章牛顿定律部分习题分析与解答 2-10一质量为m的小球最初位于如图2-10(a)所示的A点, 然后沿半径为r的光滑圆轨道ADCB下滑。试求小球到 达点C时的角速度和对圆轨道的作用力。 分新:该题可由牛顿第二定律求解。在取自然坐标的 情沉下,沿圆弧方向的加速度就是切向加速度 a,与其相对应的外力F是重力的切向分量 mgsin,而与法向加速度an相对应的外力是支 持力FN和重力的法向分量mgcos o.由此,可分 别列出切向和法向的动力学方程F=mdv/dt和 F.=ma·由于小球在滑动过程中加速度不是恒 定的,因此,需应用积分求解,为使运算简便, 可转换积分变量
第二章 牛顿定律部分习题分析与解答 2-10一质量为m的小球最初位于如图2-10(a)所示的A点, 然后沿半径为r的光滑圆轨道ADCB下滑。试求小球到 达点C时的角速度和对圆轨道的作用力。 该题可由牛顿第二定律求解。在取自然坐标的 情况下,沿圆弧方向的加速度就是切向加速度 at,与其相对应的外力Ft是重力的切向分量 mgsinα,而与法向加速度an相对应的外力是支 持力FN和重力的法向分量mgcos α.由此,可分 别列出切向和法向的动力学方程Ft=mdv/dt和 Fn=man .由于小球在滑动过程中加速度不是恒 定的,因此,需应用积分求解,为使运算简便, 可转换积分变量