
第七章排列试验 第一节排序检验法 比较数个样品,按照其某项品质程度(如,某特性的强度或嗜好程度等)的大小进行排 序的方法,成为排序检验法。该法只排出样品的次序,表明样品之间的相对大小、强弱、好 坏等等,属于程度上的差异,而不评价样品间的差异大小。此法的优点是可利用同一样品, 对其各类特征进行检验,排出优劣,且方法较简单,结果可高,即使样品间差别很小,只要 评价员很认真,或者具有一定的检验能力,都能在相当精确的程度上排出顺序。 当试验目的是就某一项性质对多个产品进行比较时,比如,甜度、新鲜程度等,使用排 序检验法是进行这种比较的最简单的方法。排序法比任何其他方法更节省时间。它常被用在 以下几个方面: 1)确定由于不同原料、加工、处理、包装和储藏等各环节而造成的产品感宫特性差异。 2)当样品需要为下一步的试验预筛或预分类,即对样品进行更精细的感官分析之前, 可应用此方法。 3)对清费者或市场经营者订购的产品的可接受性调查。 4)企业产品的精选过程。 5)可用于品评员的选择和培训。 一、方法特点 1.此法的试验原则是:以均衡随机的顺序将样品呈送给品评员,要求品评员就指 定指标将样品进行排序,计算序列和,然后利用Friedman法等对数据进行统计 分析。 2.参加试验的人数不得少于8人,如果参加人数在16以上,区分效果会得到明 显效果。根据试验目的,品评人员要有区分样品指标之间细微差别的能力。 3.当评定少量样品的复杂特性时,选用此法是快速而又高效的。此时的样品数 般小于6个。 4.但样品数量较大(如大于20个),且不是比较样品间的差别大小时,选用此法 也具有一定优势。但其信息量却不如定级法大,此法可不设对照样,将两组结
1 第七章 排列试验 第一节 排序检验法 比较数个样品,按照其某项品质程度(如,某特性的强度或嗜好程度等)的大小进行排 序的方法,成为排序检验法。该法只排出样品的次序,表明样品之间的相对大小、强弱、好 坏等等,属于程度上的差异,而不评价样品间的差异大小。此法的优点是可利用同一样品, 对其各类特征进行检验,排出优劣,且方法较简单,结果可高,即使样品间差别很小,只要 评价员很认真,或者具有一定的检验能力,都能在相当精确的程度上排出顺序。 当试验目的是就某一项性质对多个产品进行比较时,比如,甜度、新鲜程度等,使用排 序检验法是进行这种比较的最简单的方法。排序法比任何其他方法更节省时间。它常被用在 以下几个方面: 1) 确定由于不同原料、加工、处理、包装和储藏等各环节而造成的产品感官特性差异。 2) 当样品需要为下一步的试验预筛或预分类,即对样品进行更精细的感官分析之前, 可应用此方法。 3) 对消费者或市场经营者订购的产品的可接受性调查。 4) 企业产品的精选过程。 5) 可用于品评员的选择和培训。 一、方法特点 1. 此法的试验原则是:以均衡随机的顺序将样品呈送给品评员,要求品评员就指 定指标将样品进行排序,计算序列和,然后利用 Friedman 法等对数据进行统计 分析。 2. 参加试验的人数不得少于 8 人,如果参加人数在 16 以上,区分效果会得到明 显效果。根据试验目的,品评人员要有区分样品指标之间细微差别的能力。 3. 当评定少量样品的复杂特性时,选用此法是快速而又高效的。此时的样品数一 般小于 6 个。 4. 但样品数量较大(如大于 20 个),且不是比较样品间的差别大小时,选用此法 也具有一定优势。但其信息量却不如定级法大,此法可不设对照样,将两组结

果直接进行对比。 5.进行检验前,应由组织者对检验提出具体的规定,对被评价的指标和准则要有 一定的理解。如对那些特性进行排列:排列的顺序是从强到弱还是从弱到强; 检验时操作要求如何:评价气味时是否需要摇晃等, 6。排序检验只能按照一种特性进行,如要求对不同的特性进行排序,则按不同的 特性安排不同的顺序。 7。在检验中,每个评价员以事先确定的顺序检验编码的样品,并安排出一个初步 顾序,然后进一步整理调整,最后确定整个系列的强弱顺序,如果实在无法区 别两种样品,则应在问答表中注明。 二、问答表设计与做法 在进行问答表的设计时,应明确评价的指标和准则,如对那些特性进行比较,是对产品 的一种特性进行排序,还是对一种产品的多种特性进行比较:排列顺序是从强到弱还是从弱 到强:要求的检验操作过程如何:是否进行感官刺激的评价,如果是,应使评价员在不同的 评价之间使用水、淡茶或无味面包等以恢复原感觉能力。排序检验法问答表的一般形式如表 7-1、表7-2. 表7】排序检验法问答表的一般形式示例 姓名 日期 产品 试验指令:品尝样品后,请根据您所感受的甜度,把样品号码填入适当的空格中(每格中必 须填一个号码)。 甜味最强 甜味最弱
2 果直接进行对比。 5. 进行检验前,应由组织者对检验提出具体的规定,对被评价的指标和准则要有 一定的理解。如对那些特性进行排列;排列的顺序是从强到弱还是从弱到强; 检验时操作要求如何;评价气味时是否需要摇晃等。 6. 排序检验只能按照一种特性进行,如要求对不同的特性进行排序,则按不同的 特性安排不同的顺序。 7. 在检验中,每个评价员以事先确定的顺序检验编码的样品,并安排出一个初步 顺序,然后进一步整理调整,最后确定整个系列的强弱顺序,如果实在无法区 别两种样品,则应在问答表中注明。 二、问答表设计与做法 在进行问答表的设计时,应明确评价的指标和准则,如对那些特性进行比较,是对产品 的一种特性进行排序,还是对一种产品的多种特性进行比较;排列顺序是从强到弱还是从弱 到强;要求的检验操作过程如何;是否进行感官刺激的评价,如果是,应使评价员在不同的 评价之间使用水、淡茶或无味面包等以恢复原感觉能力。排序检验法问答表的一般形式如表 7-1、表 7-2。 表 7-1 排序检验法问答表的一般形式示例 姓名 日期 产品 试验指令;品尝样品后,请根据您所感受的甜度,把样品号码填入适当的空格中(每格中必 须填一个号码)。 甜味最强 甜味最弱

表7-2排序检验法问答表的一般形式 排序检验法 姓名: 日期: 试验指令: 1.从左到右依次品尝样品A、B、C、D。 2.品尝之后,就指定的特性方面进行排序。 试验结果: 样 次 2 3 4 品评员 6 三、结果分析与判断 在试验中,尽量同时提供样品,品评员同时收到以均衡、随机顺序挂列的样品。其任务 就是将样品排序。同一组样品还可以以不同的编号被一次或数次呈送,如果每组样品被评价 的次数大于2,那么试验的准确性会得到最大提高。在倾向性试验中,告诉参评人员,最喜 欢的样品排在第一位,第二喜欢的样品排在第二位,依次类推,不要把顺序搞颠倒。如果相 邻两个样品的顺序无法确定,鼓励品评员去猜测,如果实在猜不出,可以取中间值,如4 个样品中,对中间两个的顺序无法确定时,就将它们都排为(2+3)2=2.5。如果需要排序 的感官指标多于一个,则对样品分别进行编号,以免发生相互影响。排出初步顺序后,若发 现不妥之处,可以重新核查并调整顺序,确定个样品在尺度线上的相应位置。 下面对实例进行分析,以便理解, (一)样品甜味排序
3 表 7-2 排序检验法问答表的一般形式 排序检验法 姓名:_ 日期:_ 试验指令: 1. 从左到右依次品尝样品 A、B、C、D。 2. 品尝之后,就指定的特性方面进行排序。 试验结果: 1 2 3 4 1 2 3 4 5 6 三、结果分析与判断 在试验中,尽量同时提供样品,品评员同时收到以均衡、随机顺序排列的样品。其任务 就是将样品排序。同一组样品还可以以不同的编号被一次或数次呈送,如果每组样品被评价 的次数大于 2,那么试验的准确性会得到最大提高。在倾向性试验中,告诉参评人员,最喜 欢的样品排在第一位,第二喜欢的样品排在第二位,依次类推,不要把顺序搞颠倒。如果相 邻两个样品的顺序无法确定,鼓励品评员去猜测,如果实在猜不出,可以取中间值,如 4 个样品中,对中间两个的顺序无法确定时,就将它们都排为(2+3)/2=2.5。如果需要排序 的感官指标多于一个,则对样品分别进行编号,以免发生相互影响。排出初步顺序后,若发 现不妥之处,可以重新核查并调整顺序,确定个样品在尺度线上的相应位置。 下面对实例进行分析,以便理解。 (一) 样品甜味排序 样 秩 次 品评员 品
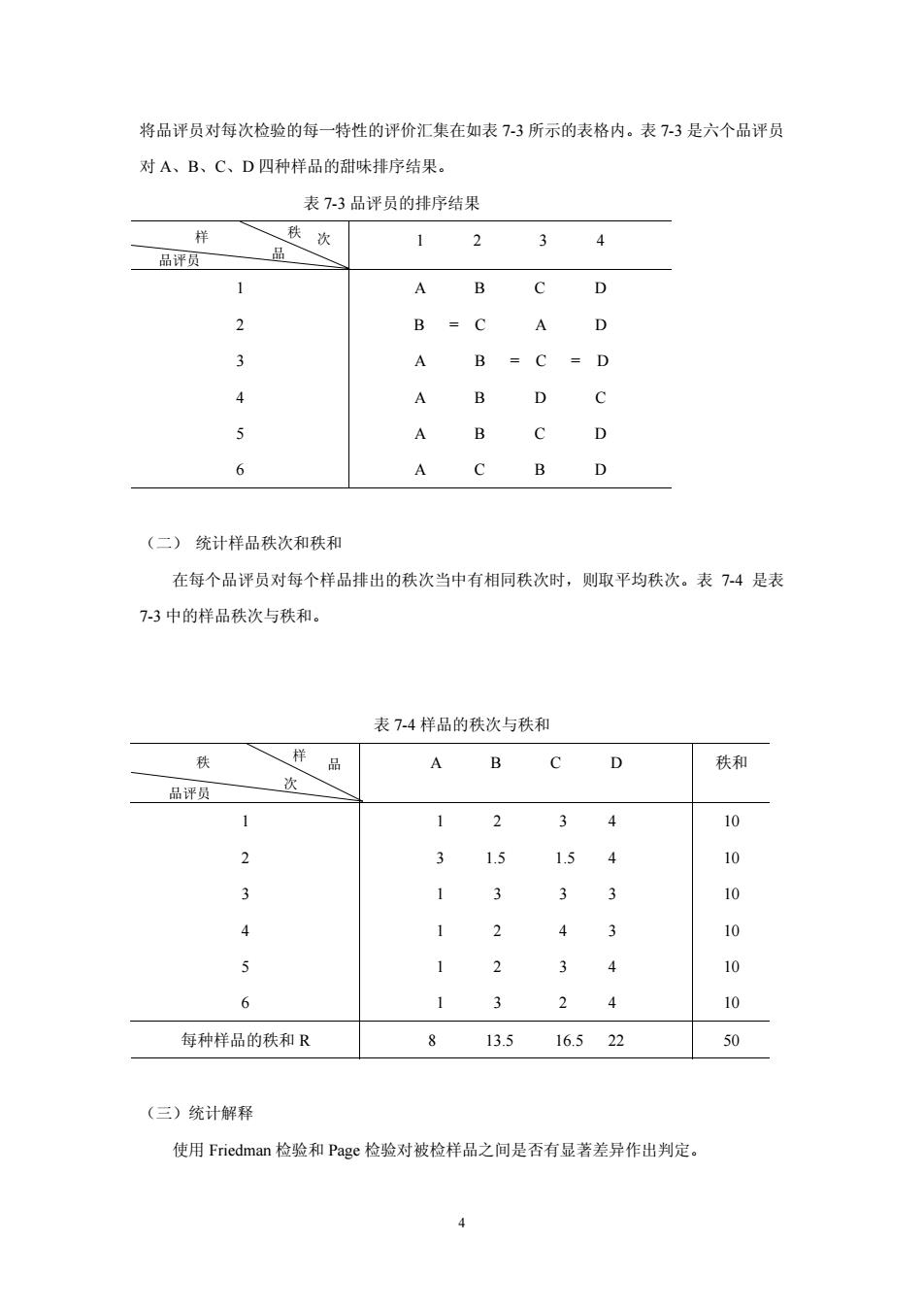
将品评员对每次检验的每一特性的评价汇集在如表7-3所示的表格内。表7-3是六个品评员 对A、B、C、D四种样品的甜味排序结果。 表73品评员的排序结果 秩次 1 2 3 4 品评 品 1 A B C D 2 B=C 3 A B =C =D 4 A B D C A B C D 6 A B D (二)统计样品秩次和秩和 在每个品评员对每个样品挂出的秩次当中有相同秩次时,则取平均秩次。表7-4是表 73中的样品秩次与秩和 表74样品的秩次与秩和 样 品 A B C D 秩和 品评员 1 1 2 34 10 1.5 1.5 4 10 3 3 3 10 ¥ 2 4 6 2 3 10 6 3 2 4 10 每种样品的秩和R 8 13516.522 50 (三)统计解释 使用Friedman检验和Page检验对被检样品之间是否有显若差异作出判定
4 将品评员对每次检验的每一特性的评价汇集在如表 7-3 所示的表格内。表 7-3 是六个品评员 对 A、B、C、D 四种样品的甜味排序结果。 表 7-3 品评员的排序结果 1 2 3 4 1 2 3 4 5 6 A B C D B = C A D A B = C = D A B D C A B C D A C B D (二) 统计样品秩次和秩和 在每个品评员对每个样品排出的秩次当中有相同秩次时,则取平均秩次。表 7-4 是表 7-3 中的样品秩次与秩和。 表 7-4 样品的秩次与秩和 A B C D 秩和 1 2 3 4 5 6 1 2 3 4 3 1.5 1.5 4 1 3 3 3 1 2 4 3 1 2 3 4 1 3 2 4 10 10 10 10 10 10 每种样品的秩和 R 8 13.5 16.5 22 50 (三)统计解释 使用 Friedman 检验和 Page 检验对被检样品之间是否有显著差异作出判定。 样 秩 次 品评员 品 样 秩 品 次 品评员

L.Friedman检验 先用下式求出统计量F: 12 Fp可+L-3P+明 式中 」—品评员数 P一样品(或产品)数 R、R、R一每种样品的秩和 查表8-5,若计算出的F值大于或等以表中对应于P、人、口的临界值:则可以判定样品之间 有显著性差异:若小于相应临界值,则可以判定样品之间没有显著性差异, 当品评员数J较大,或当样品数P大于5时,超出表7-5的范围,可查x2分布表(附表1), F值近似服从自由度为P1的x2值 上例中(见表7-4))的F值为: 12 F6x4x4+8+1353+1653+22-3x6x4+明 =10.25 当品评员是在分不出某两种样品之间的差距时,可以允许将这两种样品排定同一秩次,这时 用F代替F: F F=1-叽P(P-叨 式中E值由如下得出: 令nnLn:为出现相同秩的样品数,若没有相同秩次,n=1,则 E=(m3-)+(n3-n)+L+(n3-n) 表中,出现相同秩次的样品数有:2=2,”,=3,其余均没有相同秩次。所以 E=(2-2+(32-3+L+(-) =6+24 =30
5 1. Friedman 检验 先用下式求出统计量 F: ( ) ( ) 22 2 1 2 12 3 1 1 F R R R JP P JP P = ++ − + ⎡ ⎤ ⎣ ⎦ + L 式中 J——品评员数 P——样品(或产品)数 R1、R2、RP——每种样品的秩和 查表 8-5,若计算出的 F 值大于或等以表中对应于 P、J、α 的临界值;则可以判定样品之间 有显著性差异;若小于相应临界值,则可以判定样品之间没有显著性差异。 当品评员数 J 较大,或当样品数 P 大于 5 时,超出表 7-5 的范围,可查 2 x 分布表(附表 1.), F 值近似服从自由度为 P-1 的 2 x 值. 上例中(见表 7-4))的 F 值为: ( ) ( ) 12 2 2 22 8 13.5 16.5 22 3 6 4 1 64 41 10.25 F = + + + −×× + ⎡ ⎤ ⎣ ⎦ ×× + = 当品评员是在分不出某两种样品之间的差距时,可以允许将这两种样品排定同一秩次,这时 用 ' F 代替 F: ( ) ' 2 1 1 F F E JP P = − − ⎡ ⎤ ⎣ ⎦ 式中 E 值由如下得出: 令 1 2 k nn n 、 、L 为出现相同秩的样品数,若没有相同秩次, 1 k n = ,则 ( )( ) ( ) 33 3 Enn n n n n = − + − ++ − 11 2 2 L k k 表中,出现相同秩次的样品数有: 2 n =2, 3 n =3,其余均没有相同秩次。所以 ( )( ) ( ) 33 3 2 2 33 11 6 24 30 E = −+ −++ − = + = L
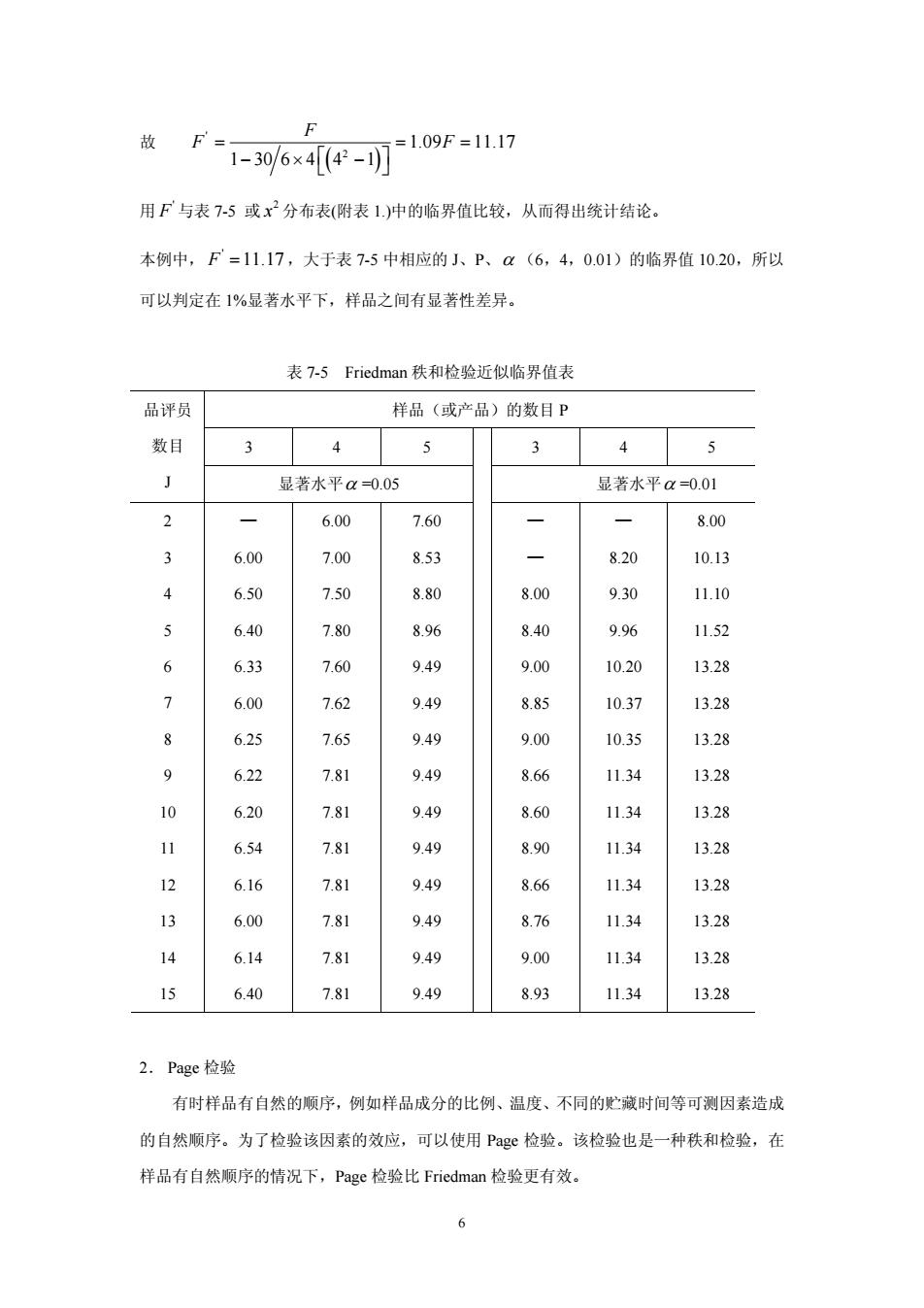
故F“1-530W6x4e-可109F-17 用F与表7-5或x分布表(附表1)中的临界值比较,从而得出统计结论。 本例中,F=11.17,大于表7-5中相应的小、P、a(6,4,0.01)的临界值10.20,所以 可以判定在1%显著水平下,样品之间有显著性差异。 表7-5 Friedman秩和检验近似临界值表 品评员 样品(或产品)的数目P 数日 3 4 5 3 45 J 显著水平a=0.05 显著水平a=0.01 2 6.00 7.60 8.00 6.00 7.00 8.53 8.20 10.13 6.50 7.50 8.80 8.00 9.30 1.10 6.40 7.80 8.96 8.40 9.96 11.52 6 6.33 7.60 9.49 9.00 10.20 13.28 60 7.62 9.49 8.85 10.37 1328 8 6.25 7.65 9.49 9.00 10.35 13.28 6.22 7.81 949 8.66 11.34 13.28 6.20 7.81 9.49 8.60 11.34 1328 6.54 18 949 890 1.34 1328 6 1 9.49 8.66 1.34 13.28 6.00 7.81 8.76 1134 1328 14 6.14 7.81 949 9.00 11.34 13.28 15 6.40 7.81 9.49 8.93 11.34 13.28 2.Page检验 有时样品有自然的顺序,例如样品成分的比例、温度、不同的贮藏时间等可测因素造成 的自然顺序。为了检验该因素的效应,可以使用Pg检验。该检验也是一种秩和检验,在 样品有自然顺序的情况下,Page检验比Friedman检验更有效
6 故 ( ) ' 2 1.09 11.17 1 30 6 4 4 1 F F F = == −× − ⎡ ⎤ ⎣ ⎦ 用 ' F 与表 7-5 或 2 x 分布表(附表 1.)中的临界值比较,从而得出统计结论。 本例中, ' F =11.17 ,大于表 7-5 中相应的 J、P、α (6,4,0.01)的临界值 10.20,所以 可以判定在 1%显著水平下,样品之间有显著性差异。 表 7-5 Friedman 秩和检验近似临界值表 样品(或产品)的数目 P 3 4 5 3 4 5 品评员 数目 J 显著水平α =0.05 显著水平α =0.01 2 3 4 5 6 7 8 9 10 11 12 13 14 15 — 6.00 6.50 6.40 6.33 6.00 6.25 6.22 6.20 6.54 6.16 6.00 6.14 6.40 6.00 7.00 7.50 7.80 7.60 7.62 7.65 7.81 7.81 7.81 7.81 7.81 7.81 7.81 7.60 8.53 8.80 8.96 9.49 9.49 9.49 9.49 9.49 9.49 9.49 9.49 9.49 9.49 — — 8.00 8.40 9.00 8.85 9.00 8.66 8.60 8.90 8.66 8.76 9.00 8.93 — 8.20 9.30 9.96 10.20 10.37 10.35 11.34 11.34 11.34 11.34 11.34 11.34 11.34 8.00 10.13 11.10 11.52 13.28 13.28 13.28 13.28 13.28 13.28 13.28 13.28 13.28 13.28 2. Page 检验 有时样品有自然的顺序,例如样品成分的比例、温度、不同的贮藏时间等可测因素造成 的自然顺序。为了检验该因素的效应,可以使用 Page 检验。该检验也是一种秩和检验,在 样品有自然顺序的情况下,Page 检验比 Friedman 检验更有效

如果、L,是以确定的顺序排列得P种样品的理论上的平均秩次,如果两种样品之间 没有差别,则应L=,·否则,应r≤r≤L≤,其中至少有一个不等式是成立的 也就是原假设不能成立,检验原假设能够成立,用下式计算统计量来确定 L=R +2R,+L +PRp 若计算出的L值大于或等于表7-6中的相应的临界值,则拒绝原假设而判定样品之间有显著 性差异。 如若品评员人数」或样品数P超出表75的范围,可用统计量汇作检验,见下式: 12L-3JP(P+1) L P(P+1)NJ(P-1) 当L≥1.65,=0.05 L≥2.33,=0.01 以此判定样品之间有显若性差异
7 如果 1 2 p rr r 、 、L 是以确定的顺序排列得 P 种样品的理论上的平均秩次,如果两种样品之间 没有差别,则应 1 2 p rr r = =L = 。否则,应 1 p rr r ≤ ≤ ≤ L ,其中至少有一个不等式是成立的, 也就是原假设不能成立,检验原假设能够成立,用下式计算统计量来确定: 1 2 2 L R R PR =+ ++ L P 若计算出的 L 值大于或等于表 7-6 中的相应的临界值,则拒绝原假设而判定样品之间有显著 性差异。 如若品评员人数 J 或样品数 P 超出表 7-5 的范围,可用统计量 ' L 作检验,见下式: ( ) ( )( ) 2 ' 12 3 1 1 1 L JP P L PP JP − + = + − 当 ' L ≥ 1.65,α =0.05 ' L ≥ 2.33,α =0.01 以此判定样品之间有显著性差异

表7-6Page检验临界值表 品评员 样品(或产品)数P 数目J 345678345678 显著水平a=0.05 显著水平a=0.01 2 28 103 166 252 362 60106173261376 3 150244 370 532 87 155 252 4 197 321 487 701 114 204 331 5 244 397 603 68 6 893 6 79 163 291 474 719 1037 81 16 299 1063 7 550 835 1204 9 563 855 32 8 214 925 % 1371 106 220 鸣 640 972 9 116 1537 9 10 26 m 1180 1703 487 793 1205 1736 11 292 852 1295 1868 14 298 6 1905 12 317 1410 2035 946 1437 2072 13 16 343 103 1525 2201 169 240 14 368 661 1018 1639 2367 p 2407 15 % 394 1153 1754 2532 194 402 721 174 2574 16 20 1228 1868 2697 206 1249 2740 17 44s 1303 1982 2862 218 453 1325 2014 2907 2 471 1378 2097l 3028 231 14 3073 19 23 496 1453 2217 3193 243 505 1476 3240 20 251 52 37 1528 2325 3358 256 531 953 1552 2360 3406 (三)统计分组 当用Friedman检验或Page检验确定了样品之间存在显著性差异之后,可采用下述方法 进一步确定个样品之间的差异程度, 1.多重比较和分组
8 表 7-6 Page 检验临界值表 样品(或产品)数 P 3 4 5 6 7 8 3 4 5 6 7 8 品评员 数目 J 显著水平α =0.05 显著水平α =0.01 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 28 41 54 66 79 91 104 116 128 141 153 165 178 190 202 215 227 239 251 58 84 111 137 163 189 214 240 266 292 317 343 368 394 420 445 471 496 522 103 150 197 244 291 338 384 431 477 523 570 615 661 707 754 800 846 891 937 166 244 321 397 474 550 925 701 777 852 928 1003 1078 1153 1228 1303 1378 1453 1528 252 370 487 603 719 835 950 1065 1180 1295 1410 1525 1639 1754 1868 1982 2097 2217 2325 362 532 701 869 1037 1204 1371 1537 1703 1868 2035 2201 2367 2532 2697 2862 3028 3193 3358 — 42 55 68 81 93 106 119 131 144 156 169 181 194 206 218 231 243 256 60 87 114 141 167 193 220 246 272 298 324 350 376 402 427 453 479 505 531 106 155 204 251 299 346 393 441 487 534 584 628 674 721 767 814 860 906 953 173 252 331 409 486 563 640 717 793 869 946 1022 1098 1174 1249 1325 1401 1476 1552 261 382 5041 620 737 855 972 1088 1205 1321 1437 1553 1668 1784 1899 2014 2130 2245 2360 376 549 722 893 1063 1232 1401 1569 1736 1905 2072 2240 2407 2574 2740 2907 3073 3240 3406 (三) 统计分组 当用 Friedman 检验或 Page 检验确定了样品之间存在显著性差异之后,可采用下述方法 进一步确定个样品之间的差异程度。 1. 多重比较和分组

根据各样品的秩和R。,从小到大将样品初步排序,上例的排序为: 813.516.522 计算临界值r(I,a): r(.a)-q(La( 12 式中g(L,a)值可查表8-7,其中: 1=23LP. 本例中,根据表7-3,临界值r(1,a)为: .a)=g0,a)V6x44+可 12 =3.16g(1,a) 比较与分组: 以下列的顺序检验这些秩和的差数:最大减最小,最大减次小,LL最大减次大:然 后次大减最小,次大减次小LL依次减下去,一直到次小减最小 Rp-Rn与r(p,a)比较: Rp-Ra与r(p-L,a)比较: Rp-RP-1与r(2,a)比较: Rp4-Ra与r(P-1,a)比较: RP-1-R2与r(P-2,a)比较: R2-Rn与r(2,a)比较 若相互比较的两个样品A,与A的秩和之差R,一R。(>)小于相应的r值,则表示这
9 根据各样品的秩和 RP ,从小到大将样品初步排序,上例的排序为: RA RB RC RD 8 13.5 16.5 22 计算临界值 r(I,α ): ()() ( ) 1 , , 12 JP P rI qI α α + = 式中 q I( ) ,α 值可查表 8-7,其中: I = 2,3,L P 。 本例中,根据表 7-3,临界值 r I( ,α ) 为: ()() ( ) ( ) 6 44 1 , , 12 3.16 , rI qI q I α α α × + = = 比较与分组: 以下列的顺序检验这些秩和的差数:最大减最小,最大减次小,L L 最大减次大;然 后次大减最小,次大减次小L L 依次减下去,一直到次小减最小; RAP A − R 1与 r p( ) ,α 比较; RAP A − R 2 与 r p( ) −1,α 比较; M R R AP AP − −1与 r( ) 2,α 比较; RAP A −1 1 − R 与 r P( ) −1,α 比较; RAP A −1 2 − R 与 r P( ) − 2,α 比较; M RA A 2 1 − R 与 r( ) 2,α 比较 若相互比较的两个样品 Aj 与 Ai 的秩和之差 RAj Ai − R (j>i)小于相应的 r 值,则表示这

两个样品以及秩和位于这两个样品之间的所有样品无显若差异,在这些样品以下可用一横线 表示,即: 4AL4, 横线内的样品不必再作比较。 若相互比较的两个样品A与A,的秩和之差R,一R大于或等于相应的r值,则表示这 两个样品有显著性差异,其下面不划横线。 不同横线上面的样品表示不同的组,若有样品处于横线重叠处,应单独列为一组。 根据表7-4,查表7-7可得: r(4,0.05)=q(4,0.05)×3.16=3.63×3.16=11.47 r(3,0.05)=q(3,0.05)×3.16=3.31×3.16=10.46 r(2,0.05)=q(2,0.05)×3.16=2.77×3.16=8.75 由于: R-R=22-8=14>r(4,0.05)=11.47,不可划线 R-R=22-13.5=8.5<r(3,0.05)=10.46,可划线。 R-R=16.5-8=8.5<r(3,0.05)=10.46,可划线。 结果如下: A B C D 最后分为3组 A B C D 结论:在5%的显著水平上,D样品最甜,C、B样品次之,A样品最不甜,C、B样品在甜 度上无显若性差别
10 两个样品以及秩和位于这两个样品之间的所有样品无显著差异,在这些样品以下可用一横线 表示,即: 横线内的样品不必再作比较。 若相互比较的两个样品 Ai 与 Aj 的秩和之差 RAj Ai − R 大于或等于相应的 r 值,则表示这 两个样品有显著性差异,其下面不划横线。 不同横线上面的样品表示不同的组,若有样品处于横线重叠处,应单独列为一组。 根据表 7-4,查表 7-7 可得: r q ( )( ) 4,0.05 4,0.05 3.16 3.63 3.16 11.47 = ×=×= r q ( )( ) 3,0.05 3,0.05 3.16 3.31 3.16 10.46 = × =× = r q ( )( ) 2,0.05 2,0.05 3.16 2.77 3.16 8.75 = ×=×= 由于: RR r 4 1 − = −= > = 22 8 14 4,0.05 11.47 ( ) ,不可划线。 RR r 4 2 −=− = < = 22 13.5 8.5 3,0.05 10.46 ( ) ,可划线。 RR r 3 1 − = −= < = 16.5 8 8.5 3,0.05 10.46 ( ) ,可划线。 结果如下: 最后分为 3 组 结论:在 5%的显著水平上,D 样品最甜,C、B 样品次之,A 样品最不甜,C、B 样品在甜 度上无显著性差别。 Ai Ai+1 L Aj