
第八章分级试验 分级试验是以某个级数值来描述食品的属性。在排列试验中,两个样品之间必须存在先 后顺序,而在分级试验中,两个样品可能属于同一级数,也可能属于不同级数,而且它们之 间的级数差别可大可小。排列试验和分级试验各有特点和针对性。 级数定义的灵活性很大,没有严格想定。例如,对食品甜度,其级数值可按下表定义 分级方法 12345 骚:},4 路甜 适中 50 }2 4 路不甜 较不甜3222 对于食品的咸度、酸度、硬度、脆性、粘性、喜欢程度或者其它指标的级数值也可以类 推。当然也可以用分数,数值范围或图解来对食品进行级数描述。例如,对于茶叶进行综合 平判的分数范围为:外形(20分).香气与滋味(60分)。水色(10分),叶底(10分).总 分100分。当总分>90分为1级茶,81~90分为2级茶,71一80分为3级茶,61一70分为 4级茶 在分级试验中,由于每组试验人员的习惯、爱好及分辨能力各不相同,使得各人的试验 数据可能不一样。因此规定标准样的级数,使它的基线相同,这样有利于统一所有试验人员 的试验结果。 第一节评分法 一、评分法特点 评分法是指按预先设定的评价基准,对试样的特性和嗜好程度以数字标度进行评定,然 后换算成得分的一种评价方法。在评分法中,所有的数字标度为等距或比率标度,如1一10 (10级),一3~3级(7级)等数值尺度。该方法不同于其它方法的是所谓的绝对性判断 即根据评价员各自的鉴评基准进行判断。它出现的粗评分现象也可由增加评价员人数的方 法来克服。 由于此方法可同时评价一种或多种产品的一个或多个指标的强度及其差异,所以应用较 为广泛。尤其用于评价新产品。 二、问答表的设计和做法 设计问答票前,首先要确定所使用的标度类型。在检验前,要使评价员对每一个评分点 所代表的意义有共同的认识。样品的出示顺序可利用拉丁法随机排列。 问答票的设计应和产品的特性及检验的目的相结合,尽最简洁明了。可参考表8-1的形
1 第八章 分级试验 分级试验是以某个级数值来描述食品的属性。在排列试验中,两个样品之间必须存在先 后顺序,而在分级试验中,两个样品可能属于同一级数,也可能属于不同级数,而且它们之 间的级数差别可大可小。排列试验和分级试验各有特点和针对性。 级数定义的灵活性很大,没有严格规定。例如,对食品甜度,其级数值可按下表定义。 对于食品的咸度、酸度、硬度、脆性、粘性、喜欢程度或者其它指标的级数值也可以类 推。当然也可以用分数,数值范围或图解来对食品进行级数描述。例如,对于茶叶进行综合 评判的分数范围为:外形(20 分),香气与滋味(60 分),水色(10 分),叶底(10 分),总 分 100 分。当总分>90 分为 1 级茶,81~90 分为 2 级茶,71~80 分为 3 级茶,61~70 分为 4 级茶。 在分级试验中,由于每组试验人员的习惯、爱好及分辨能力各不相同,使得各人的试验 数据可能不一样。因此规定标准样的级数,使它的基线相同,这样有利于统一所有试验人员 的试验结果。 第一节 评分法 一、评分法特点 评分法是指按预先设定的评价基准,对试样的特性和嗜好程度以数字标度进行评定,然 后换算成得分的一种评价方法。在评分法中,所有的数字标度为等距或比率标度,如 1~10 (10 级),-3~3 级(7 级)等数值尺度。该方法不同于其它方法的是所谓的绝对性判断, 即根据评价员各自的鉴评基准进行判断。它出现的粗糙评分现象也可由增加评价员人数的方 法来克服。 由于此方法可同时评价一种或多种产品的一个或多个指标的强度及其差异,所以应用较 为广泛。尤其用于评价新产品。 二、问答表的设计和做法 设计问答票前,首先要确定所使用的标度类型。在检验前,要使评价员对每一个评分点 所代表的意义有共同的认识。样品的出示顺序可利用拉丁法随机排列。 问答票的设计应和产品的特性及检验的目的相结合,尽量简洁明了。可参考表 8-1 的形 极 甜 很 甜 较 甜 略 甜 适 中 略不甜 较不甜 很不甜 极不甜 分级方法 1 2 3 4 5 9 4 8 8 3 7 7 2 6 6 6 1 5 5 5 0 4 4 4 -1 3 3 3 -2 2 2 2 -3 1 1 -4 0 7 4 3 2 1 1
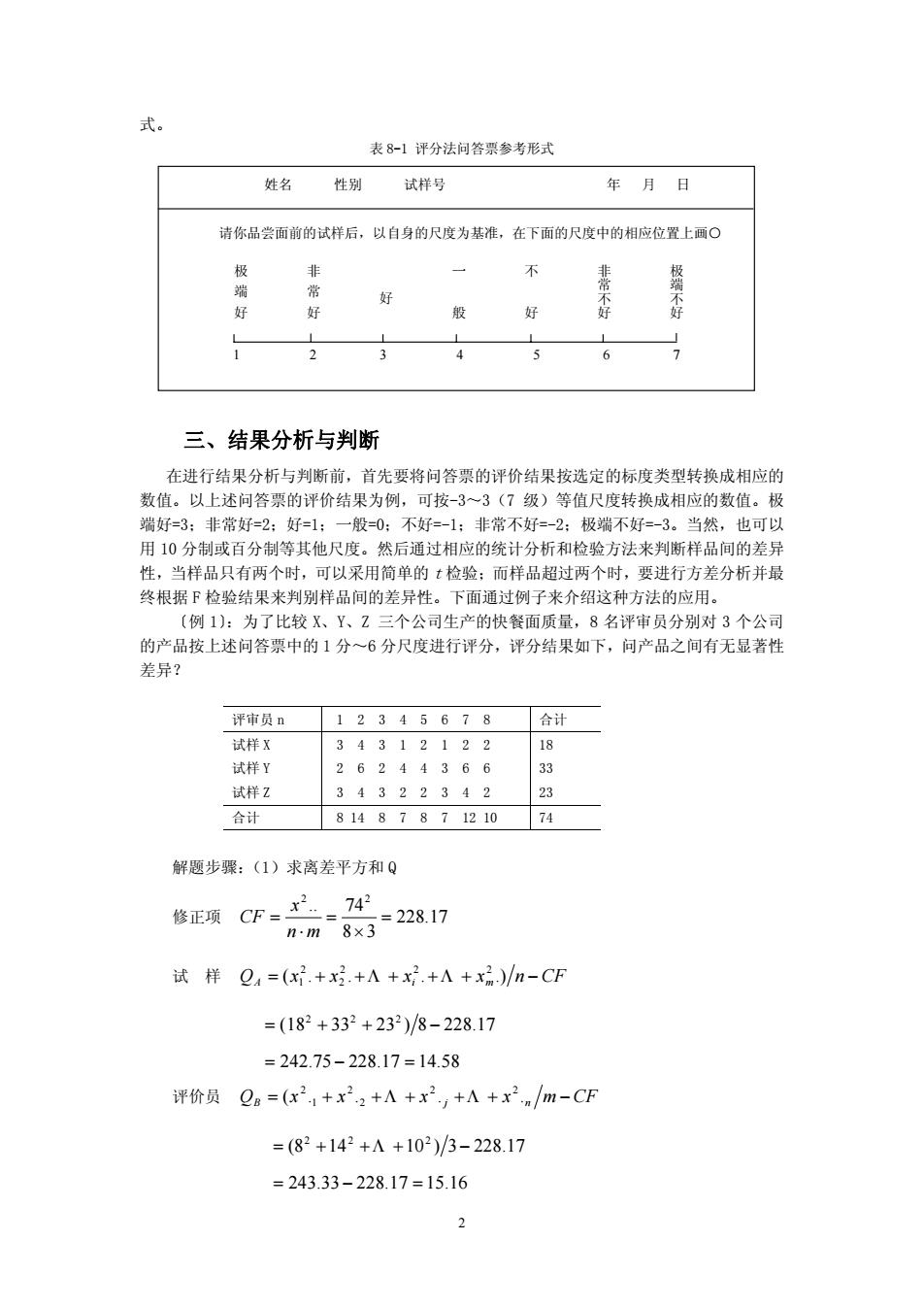
表8-1评分法问答票参考形式 姓名 性别 试样号 年月日 请你品尝面前的试样后,以自身的尺度为基准,在下面的尺度中的相应位置上画○ 不 常 好 好 好 好 2 3 4 5 6 三、结果分析与判断 在进行结果分析与判断前,首先要将问答票的评价结果按选定的标度类型转换成相应的 数值。以上述问答票的评价结果为例,可按-3~3(7级)等值尺度转换成相应的数值。极 端好=3:非常好=2:好=1:一般=0:不好=-1:非常不好=-2:极端不好=-3。当然,也可以 用10分制或百分制等其他尺度。然后通过相应的统计分析和检验方法来判断样品间的差异 当样品只有两个时,可以采用简单的t检验:而样品超过两个时,要进行方差分析并最 终根据F检验结果来判别样品间的差异性。下面通过例子来介绍这种方法的应用。 〔例1):为了比较X、Y、Z三个公司生产的快餐面质量,8名评审员分别对3个公司 的产品按上述问答票中的1分~6分尺度进行评分,评分结果如下,问产品之间有无显著性 差异? 评审员n 12345678 合计 试样X 34312122 18 试择y 26244366 33 试样Z 143ヮ9349 合计 81487871210 74 解题步環:(1)求离差平方和Q 修正项CF= -m8x32817 742 试样Q,=(x2.+x.+A+x2.+A+x2)/n-CF =(182+332+232)/8-22817 =242.75-228.17=14.58 评价员Qa=(x2+x22+A+x2,+Λ+x2n/m-CF =(82+142+Λ+102)/3-228.17 =243.33-228.17=15.16
2 式。 表 8-1 评分法问答票参考形式 三、结果分析与判断 在进行结果分析与判断前,首先要将问答票的评价结果按选定的标度类型转换成相应的 数值。以上述问答票的评价结果为例,可按-3~3(7 级)等值尺度转换成相应的数值。极 端好=3;非常好=2;好=1;一般=0;不好=-1;非常不好=-2;极端不好=-3。当然,也可以 用 10 分制或百分制等其他尺度。然后通过相应的统计分析和检验方法来判断样品间的差异 性,当样品只有两个时,可以采用简单的 t 检验;而样品超过两个时,要进行方差分析并最 终根据 F 检验结果来判别样品间的差异性。下面通过例子来介绍这种方法的应用。 〔例 1〕:为了比较 X、Y、Z 三个公司生产的快餐面质量,8 名评审员分别对 3 个公司 的产品按上述问答票中的 1 分~6 分尺度进行评分,评分结果如下,问产品之间有无显著性 差异? 评审员 n 1 2 3 4 5 6 7 8 合计 试样 X 试样 Y 试样 Z 3 4 3 1 2 1 2 2 2 6 2 4 4 3 6 6 3 4 3 2 2 3 4 2 18 33 23 合计 8 14 8 7 8 7 12 10 74 解题步骤:(1)求离差平方和 Q 修正项 228.17 8 3 . 74 2 2 = × = ⋅ = n m x CF 试 样 QA = (x . + x . + + xi . + + xm .) n − CF 2 2 2 2 2 1 Λ Λ (18 33 23 ) 8 228.17 2 2 2 = + + − = 242.75 − 228.17 = 14.58 评价员 QB = (x . + x . + + x . j + + x .n m − CF 2 2 2 2 1 2 Λ Λ (8 14 10 ) 3 228.17 2 2 2 = Λ + + + − = 243.33 − 228.17 = 15.16 姓名 性别 试样号 年 月 日 请你品尝面前的试样后,以自身的尺度为基准,在下面的尺度中的相应位置上画○ 1 2 3 4 5 6 7 不 非常不好 极端不好 好 一 般 好 非 常 好 极 端 好

总平方和Q,=(x品+x+A+x+A+x)-CF =(32+42+Λ+22)-228.17=47.83 误差QE=Q,-Q4-Q。=18.09 (2)求自由度f 试样f= -1=3-1=9 评审员 f=n-1=8-1=7 总自由度f:=m×n-1=24-1=23 误差fe=f-fa-f=14 (3)方差分析 求平均离差平方和V=Q/f=14.58/27.29 f15. 6/7=2.17 V=Q/f=18.09/14=1.29 求FoF=Vx/V=7.29/1.29=5.65 F=V/V=2.7/1.29=1.68 查F分布表(附表7.),求F(E,a)。若Fo>F(任,f,a),则对信度a,有显著性 差 本例中,P=5.65>F(2,14,0.05)=3.74 F=1.68<F(7,14,0.05)=2.76 故对信度α=5%,产品之间有显著性差异,而评价员之间无显著性差异。 将上述计算结果列入下列方差分析表。 方差来源平方和Q自由度F均方和VFo 岛A 14.58 7.29 5.65 F(2,14,0.05)=3.74 评审员B 15.16 2.17 1.68 F(7,14.0.05)=2.76 误差E 18.0g 14 1.29 合计 47083 23 (4)检验试样间显著性差异 方差分析结果,试样之间有显著性差异时,为了检验哪几个试样间有显著性差异,采用 重范围试验法,即 求试样平均分 18/8=2.2533/8=4.1323/8=2.88 按大小顺序排列: 1位 2位 3位 X 4.13 2.88 2.25 求试样平均分的标准误差:dE=√E/n=V29/8=0.4 查斯图登斯化范用表(附表8.),求斯图登斯化范围印,计算显著性差异最小范用 p=pX标准误差dE 2 3
3 总平方和 QT = (x + x + + xij + + xmn ) − CF 2 2 2 12 2 11 Λ Λ (3 4 2 ) 228.17 47.83 2 2 2 = Λ + + + − = 误 差 = − − = 18.09 QE QT QA QB (2)求自由度 f 试 样 fA=m-1=3-1=2 评审员 fB=n-1=8-1=7 总自由度 fT=m×n-1=24-1=23 误 差 fE=fT-fA-fB=14 (3)方差分析 求平均离差平方和 VA=QA/fA=14.58/2=7.29 VB=QB/fB=15.16/7=2.17 VE=QE/fE=18.09/14=1.29 求 Fo FA=VA/VE=7.29/1.29=5.65 FB=VB/VE=2.7/1.29=1.68 查 F 分布表(附表 7.),求 F(f,fE,α)。若 Fo>F(f,fE,α),则对信度 α,有显著性 差异。 本例中,FA=5.65>F(2,14,0.05)=3.74 FB=1.68<F(7,14,0.05)=2.76 故对信度 α=5%,产品之间有显著性差异,而评价员之间无显著性差异。 将上述计算结果列入下列方差分析表。 方差来源 平方和 Q 自由度 f 均方和 V Fo F 产 品 A 评审员 B 误 差 E 14.58 15.16 18.09 2 7 14 7.29 2.17 1.29 5.65*、 1.68 F(2,14,0.05)=3.74 F(7,14,0.05)=2.76 合 计 47083 23 (4)检验试样间显著性差异 方差分析结果,试样之间有显著性差异时,为了检验哪几个试样间有显著性差异,采用 重范围试验法,即 求试样平均分: X Y Z 18/8 =2.25 33/8=4.13 23/8=2.88 按大小顺序排列: 1 位 2 位 3 位 Y Z X 4.13 2.88 2.25 求试样平均分的标准误差: dE = V / n = 1.29/8 = 0.4 E 查斯图登斯化范围表(附表 8.),求斯图登斯化范围 rp,计算显著性差异最小范围 Rp=rp×标准误差 dE P 2 3

p(5%f=14)3.03 3.70 1.21 1.48 1位-3位=4.13-2.25=1.88>1.48(R) 1位-2位=4.13-2.88=1.25>1.21(R) 即1位(Y)和2、3位(Z,X)之间有显著性差异 2位-3位=2.88-2.25=0.63<1.21(R) 即2位(2)和3位(X)之间无显若性差异 故对信度a=5%,产品Y和产品X、Z比较有显著性差异,产品Y明显不好。 第二节成对比较法 一、成对比较法特点 当试样数n很大时,一次把所有的试样进行比较是困难的。此时,一般采用将n个试 样2个一组、2个一组地加以比较,根据其结果,最后对整体进行综合性的相对评价,判断 全体的优劣,从而得出数个样品相对结果的评价方法这种方法称为成对比较法。本法的优点 很多,如在顺序法中出现样品的制备及试验实施过程中的困难等大部分都可以得到解决,并 且在实验时间上,长达数日进行也无妨。 因此,本法是最近应用最广 乏的方法之 。如舍菲 (Sce)成对比较法,其特点是不仅回答了两个试样中“喜欢哪个”,即排列两个试样的 顺序,而且还要按设定的评价基准回答“喜欢到何种程度”,即评价试样之间的差别程度(相 对差)。 成对比较法可分为定向成对比较法(2选项必洗法)和差别成对比较法(简单差别检验 或异同检验)。二者在适用条件及样品呈送顺序等方面都存在一定差别。 二、问答表的设计和做法 设计问答票时,首先应根据检验目的和样品特性确定是采用定向还是差别成对比较法。 由于该方法主要是在样品两两比较时用于鉴评两个样品是否存在差异,故问答票应便于评价 员表述样品间的差异,最好能将差异的程度尽可能准确地表达出来。同时还要尽量简洁明了 可参考表8-2所给的形式。 定向成对比较法用于确定两个样品在某一特定方面是否存在差异,如甜度、色彩等。对 试验实施人要求:将两个样品同时呈送给评价员,要求评价员识别出在这一指标感官属性上 程度较高的样品。样品有两种可能的呈送顺序(B,BA),这些顺序应在评价员间随机处理, 评价员先收到样品A或样品B的概率应相等:感官专业人员必须保证两个样品只在单一的所 指定的感官方面有所不同。此点应特别 参数的改变会影响 品的许多其他感官特 性。例如,在蛋糕生产 中将的含量改变后,不只影明甜度,也会影啊蛋糕的质地和须色 对评价员的要求:必须准确理解感官专业人员所指的特定属性的含义,应在识别指定的感官 属性方面受过训练。 差别成对比较法使用条件是:没有指定可能存在差异的方面,实验者根要确定两种样品 的不同。该方法类似于3点检验或2-3点检验 但不经常采用 及3个样品。 当产 供应 不早 可行时,最好采用它来代替 2-3 施人员的要求:同时被呈送两个样品,要求回答样品是相同还是不同。差别成对比较法有4 种可能的样品呈送顺序(AA,AB,BA,BB)。这些顺序应在评价员中交叉进行随机处理,每 种顺序出现的次数相同。对评价员的要求:只需比较两个样品,判断它们是相似还是不同
4 rp(5%f=14) Rp 3.03 3.70 1.21 1.48 1 位-3 位=4.13-2.25=1.88>1.48(R3) 1 位-2 位=4.13-2.88=1.25>1.21(R2) 即 1 位(Y)和 2、3 位(Z,X)之间有显著性差异。 2 位-3 位=2.88-2.25=0.63<1.21(R2) 即 2 位(Z)和 3 位(X)之间无显著性差异。 故对信度 α=5%,产品 Y 和产品 X、Z 比较有显著性差异,产品 Y 明显不好。 第二节 成对比较法 一、成对比较法特点 当试样数 n 很大时,一次把所有的试样进行比较是困难的。此时,一般采用将 n 个试 样 2 个一组、2 个一组地加以比较,根据其结果,最后对整体进行综合性的相对评价,判断 全体的优劣,从而得出数个样品相对结果的评价方法这种方法称为成对比较法。本法的优点 很多,如在顺序法中出现样品的制备及试验实施过程中的困难等大部分都可以得到解决,并 且在实验时间上,长达数日进行也无妨。因此,本法是最近应用最广泛的方法之一。如舍菲 (Scheffe)成对比较法,其特点是不仅回答了两个试样中“喜欢哪个”,即排列两个试样的 顺序,而且还要按设定的评价基准回答“喜欢到何种程度”,即评价试样之间的差别程度(相 对差)。 成对比较法可分为定向成对比较法(2-选项必选法)和差别成对比较法(简单差别检验 或异同检验)。二者在适用条件及样品呈送顺序等方面都存在一定差别。 二、问答表的设计和做法 设计问答票时,首先应根据检验目的和样品特性确定是采用定向还是差别成对比较法。 由于该方法主要是在样品两两比较时用于鉴评两个样品是否存在差异,故问答票应便于评价 员表述样品间的差异,最好能将差异的程度尽可能准确地表达出来。同时还要尽量简洁明了。 可参考表 8-2 所给的形式。 定向成对比较法用于确定两个样品在某一特定方面是否存在差异,如甜度、色彩等。对 试验实施人要求:将两个样品同时呈送给评价员,要求评价员识别出在这一指标感官属性上 程度较高的样品。样品有两种可能的呈送顺序(AB,BA),这些顺序应在评价员间随机处理, 评价员先收到样品 A 或样品 B 的概率应相等;感官专业人员必须保证两个样品只在单一的所 指定的感官方面有所不同。此点应特别注意,一个参数的改变会影响产品的许多其他感官特 性。例如,在蛋糕生产中将糖的含量改变后,不只影响甜度,也会影响蛋糕的质地和颜色; 对评价员的要求:必须准确理解感官专业人员所指的特定属性的含义,应在识别指定的感官 属性方面受过训练。 差别成对比较法使用条件是:没有指定可能存在差异的方面,实验者想要确定两种样品 的不同。该方法类似于 3 点检验或 2-3 点检验,但不经常采用。当产品有一个延迟效应或是 供应不足以及 3 个样品同时呈送不可行时,最好采用它来代替 3 点检验或 2-3 点检验。对实 施人员的要求:同时被呈送两个样品,要求回答样品是相同还是不同。差别成对比较法有 4 种可能的样品呈送顺序(AA,AB,BA,BB)。这些顺序应在评价员中交叉进行随机处理,每 种顺序出现的次数相同。对评价员的要求:只需比较两个样品,判断它们是相似还是不同
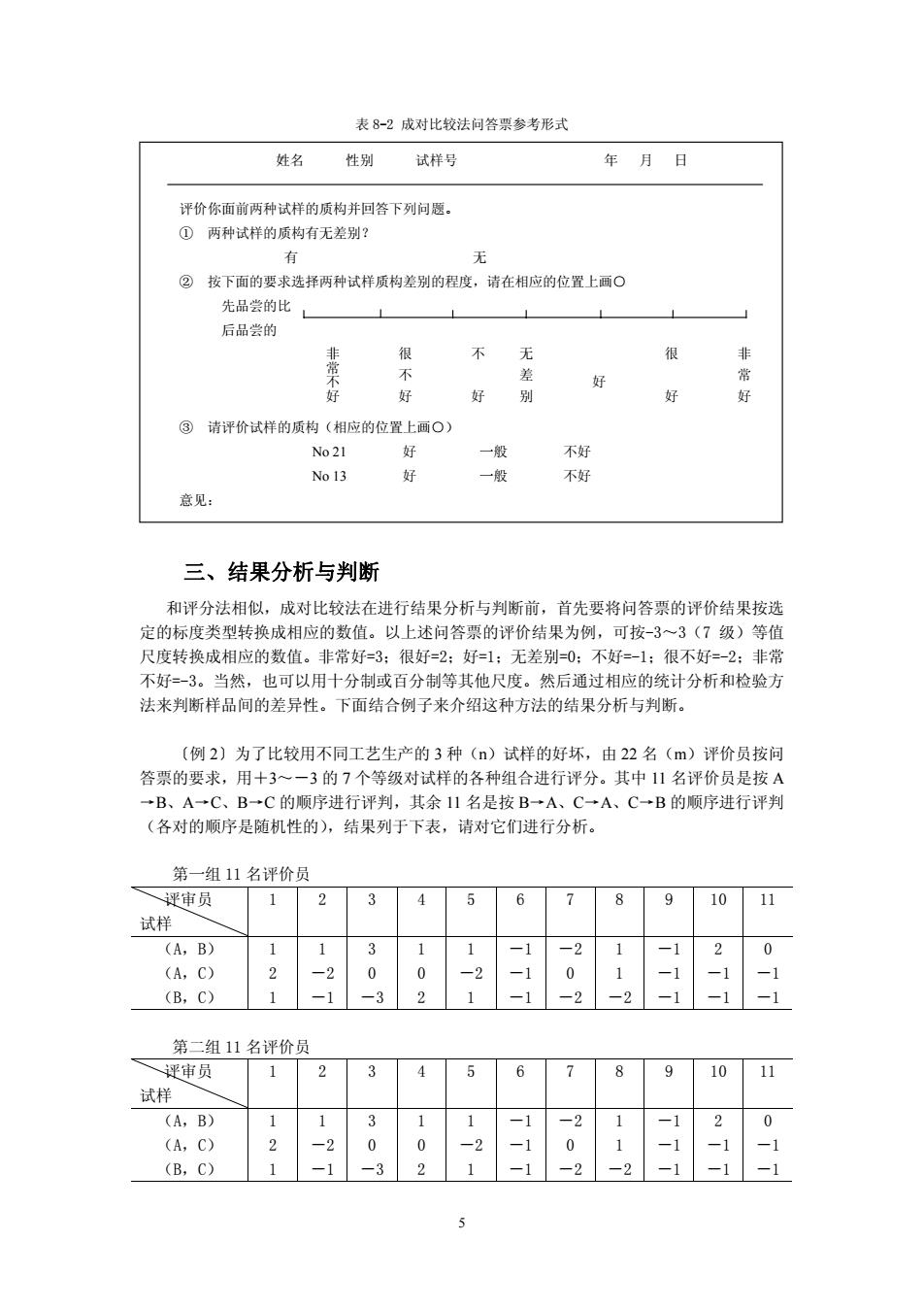
表8-2成对比较法问答票参考形式 姓名 性别试样号 年月日 评价你面前两种试样的质构并回答下列问题 ①两种试样的质构有无差别? ②按下面的要求选择两种试样质构差别的程度,请在相应的位置上画○ 先品尝的比 后品尝的 悲 很 不无 很 好 好 别 ©请评价试样的质构(相应的位置上商○) No 21 好 一般 不好 No13 好 一股 不好 意见: 三、结果分析与判断 和评分法相似,成对比较法在进行结果分析与判断前,首先要将问答票的评价结果按选 定的标度类型转换成相应的数值。以上述问答票的评价结果为例,可按-3一3(7级)等值 尺度转换成相应的数值。非常好=3:很好=2:好=1:无差别=0:不好=-1:很不好=-2:非常 不好=-3。当然,也可以用十分制或百分制等其他尺度。然后通过相应的统计分析和检验方 法来判断样品间的差异性。下面结合例子来介绍这种方法的结果分析与判断 (例2)为了比较用不同工艺生产的3种(n)试样的好坏,由22名(m)评价员按问 答票的要求,用+3~一3的7个等级对试样的各种组合进行评分。其中11名评价员是按A →B、A→C、B→C的顺序进行评判,其余11名是按B一A、C一A、C一B的顺序进行评判 (各对的顺序是随机性的),结果列于下表,请对它们进行分析。 第一组11名评价员 评审员 2 34567 891011 试 (A,B) 0 (A,C) 2 0 (B,C) 1 -1 一2 第二组11名评价员 审员 2 3 4567891011 (A,B) 1 -21 -1 20 (A.C) 0 1 -1 (B,C) 1 1
5 表 8-2 成对比较法问答票参考形式 三、结果分析与判断 和评分法相似,成对比较法在进行结果分析与判断前,首先要将问答票的评价结果按选 定的标度类型转换成相应的数值。以上述问答票的评价结果为例,可按-3~3(7 级)等值 尺度转换成相应的数值。非常好=3;很好=2;好=1;无差别=0;不好=-1;很不好=-2;非常 不好=-3。当然,也可以用十分制或百分制等其他尺度。然后通过相应的统计分析和检验方 法来判断样品间的差异性。下面结合例子来介绍这种方法的结果分析与判断。 〔例 2〕为了比较用不同工艺生产的 3 种(n)试样的好坏,由 22 名(m)评价员按问 答票的要求,用+3~-3 的 7 个等级对试样的各种组合进行评分。其中 11 名评价员是按 A →B、A→C、B→C 的顺序进行评判,其余 11 名是按 B→A、C→A、C→B 的顺序进行评判 (各对的顺序是随机性的),结果列于下表,请对它们进行分析。 第一组 11 名评价员 评审员 试样 1 2 3 4 5 6 7 8 9 10 11 (A,B) (A,C) (B,C) 1 2 1 1 -2 -1 3 0 -3 1 0 2 1 -2 1 -1 -1 -1 -2 0 -2 1 1 -2 -1 -1 -1 2 -1 -1 0 -1 -1 第二组 11 名评价员 评审员 试样 1 2 3 4 5 6 7 8 9 10 11 (A,B) (A,C) (B,C) 1 2 1 1 -2 -1 3 0 -3 1 0 2 1 -2 1 -1 -1 -1 -2 0 -2 1 1 -2 -1 -1 -1 2 -1 -1 0 -1 -1 姓名 性别 试样号 年 月 日 评价你面前两种试样的质构并回答下列问题。 ① 两种试样的质构有无差别? 有 无 ② 按下面的要求选择两种试样质构差别的程度,请在相应的位置上画○ 先品尝的比 后品尝的 ③ 请评价试样的质构(相应的位置上画○) No 21 好 一般 不好 No 13 好 一般 不好 意见: 非 常 好 很 好 好 无 差 别 不 好 很 不 好 非常不好

解:(1)整理试验数据,求总分,嗜好度山,平均嗜好度花,(除去顺序效果的部分) 和顺序效果6,。 评分 -3 一2 1 0 1 2 3 总分 组合 (A.B) 0.545 0.045 (B,A) 45 (A,C) -0.455 -0.955 (C,A) 3 1 16 1.455 (B,C) 1 2 5 2 1 -8 -0.727 -0.636 (C.B) 0.545 合计1718815116 其中总分=(-2)×1+(-1)×2+0×1+1×5+2×1+3×1=6 4=总分/得分个数=6/11=0.545 ,=2d,-2)=号x0.545-045)=0.045 按照同样的方法计算其他各行的相应数据,并将计算结果列于上表。 (2)求各试样的主效果a a4=4++c)=0+0.045-0.95)=-0.303 a=d+m+c)=-0.045+0-0.636)=-0227 ae=d。++)=0.955+0.636+0)=0530 3)求平方和 总平方和Q=3'×(1+6)+22×(7+11)+1×(18+15)-168 主效果产生的平方和Q阳=主效果平方和×试样数×评价员数: 0.=22×3×(0.303+0.2272+0.530)=28.0 平均嗜好度产生的平方和Q。-∑?×评价员数 0.=22×(0.045+0.955+0.636)=29.0 离差平方和Q=Q.一Q=1.0 平均效果Q。=平均平方和×评价员数的一半 Q.=11×(0.5452+0.4552+(-0.455)2+1.4552+(-0.727)2+0.545)=40.2 面序效果0.=0.-0.=402一29.0=11.2 误差平方和0=0,-Q.=168-40.2=127.8 (4)求自由度
6 解:(1)整理试验数据,求总分,嗜好度 μij ) ,平均嗜好度π ij ) (除去顺序效果的部分) 和顺序效果δ ij 。 评分 组合 -3 -2 -1 0 1 2 3 总分 μij ) π ij ) (A,B) (B,A) 1 2 4 1 2 5 3 1 1 2 6 5 0.545 0.455 0.045 (A,C) (C,A) 2 4 3 2 1 3 1 5 1 -5 16 -0.455 1.455 -0.955 (B,C) (C,B) 1 2 2 5 3 2 1 1 3 2 -8 6 -0.727 0.545 -0.636 合计 1 7 18 8 15 11 6 其中 总分=(-2)×1+(-1)×2+0×1+1×5+2×1+3×1=6 μij ) =总分/得分个数=6/11=0.545 π ij ) (0.545 0.455) 0.045 2 1 ( ) 2 1 = μij − μ ji = × − = ) ) 按照同样的方法计算其他各行的相应数据,并将计算结果列于上表。 (2)求各试样的主效果 αi (0 0.045 0.955) 3 1 ( ) 3 1 α A = π AA + π AB + π AC = + − ) ) ) = −0.303 ( 0.045 0 0.636) 3 1 ( ) 3 1 α B = π BA + π BB + π BC = − + − ) ) ) = −0.227 (0.955 0.636 0) 3 1 ( ) 3 1 α C = π CA + π CB + π CC = + + ) ) ) = 0.530 (3)求平方和 总平方和 QT=32 ×(1+6)+22 ×(7+11)+12 ×(18+15)=168 主效果产生的平方和 Qa=主效果平方和×试样数×评价员数: Qa=22×3×(0.3032 +0.2272 +0.5302 )=28.0 平均嗜好度产生的平方和Qπ = ∑π i 2 ×评价员数 ) Qπ=22×(0.0452 +0.9552 +0.6362 )=29.0 离差平方和 QT=Qπ-Qa=1.0 平均效果 Qμ=平均平方和×评价员数的一半 Qμ=11×〔0.5452 +0.4552 +(-0.455)2 +1.4552 +(-0.727)2 +0.5452 〕=40.2 顺序效果 Qδ=Qμ-Qπ=40.2-29.0=11.2 误差平方和 QE=QT-Qμ=168-40.2=127.8 (4)求自由度 f

f=n-1=3-1=2 万=a-1a-2=6-xg-2=1 方=-=×3xB-=3 f。=n(n-1)=3×(3-1)=6 f=n-9-=3x3-1)x1-)=60 元=n-%=3x3-x11=66 (5)作方差分析表 方差来源 平方和Q自由度f均方和VFo F 主效果a 28.0 2 14.0 6.57F(2,60,0.01)=4.98 离差r 1.0 1.0 0.47 F(1,60.0.05)=4.0 平均嗜好度 290 F(3,60,0.05)=2.76 顺序效果8 11.2 3.7 1.74 平均口 40.2 6 误差E 127.8 60 2.13 合计 168 66 求下0的结果表明,对信度ā=1%,主效果有显若性差异,离差和顺序效果无显著性差 异。即A、B、C之间的好坏很明确,只用主效果表示也足够(如下图所示): -05-03-0100i+0305 (6)主效果差(a,一a) 先求,s=9asV误差均方和评价员数×试样数 其中qas=3.4(查附表8.斯图登斯化范用=3,f=60),所以 2.13 s=34×2×)=0612 a4-aR=卜0.303+0227=0.076as,故A、C之间有显著性差异 ag-ac=卜0.227-0.530=0.757>Y%s,故B、C之间有显著性差异. 结论:对信度a=5%,A和B之间无差异,A和C,B和C之间有差异
7 3 (3 1) 11 66 2 ( 1) 1) 3 (3 1) (11 1) 60 2 ( 1)( ( 1) 3 (3 1) 6 3 (3 1) 3 2 1 ( 1) 2 1 ( 1) 3 2 1 (3 1) (3 2) 1 2 1 ( 1)( 2) 2 1 1 3 1 2 = − = × − × = = − − = × − × − = = − = × − = = − = × × − = = − = = − − = × − × − = = − = − = m f n n m f n n f n n f n n f n n fr n n f n T E a μ δ π (5)作方差分析表 方差来源 平方和 Q 自由度 f 均方和 V Fo F 主效果α 离差 r 28.0 1.0 2 1 14.0 1.0 6.57** 0.47 F(2,60,0.01)=4.98 F(1,60,0.05)=4.0 平均嗜好度π 顺序效果δ 29.0 11.2 3 3 3.7 1.74 F(3,60,0.05)=2.76 平均μ 误差 E 40.2 127.8 6 60 2.13 合计 168 66 求 Fo 的结果表明,对信度α=1%,主效果有显著性差异,离差和顺序效果无显著性差 异。即 A、B、C 之间的好坏很明确,只用主效果表示也足够(如下图所示): (6)主效果差(αi-αj) 先求Y0.05 = q0.05 误差均方和(评价员数×试样数) 其中 q0.05=3.4(查附表 8.斯图登斯化范围 n=3,f=60),所以 0.612 (22 3) 2.13 0.05 3.4 = × Y = × 0.05 α A −α B = − 0.303 + 0.227 = 0.076 Y ,故A、C之间有显著性差异。 0.05 α B −α C = − 0.227 − 0.530 = 0.757 > Y ,故B、C之间有显著性差异。 结论:对信度α=5%,A和B之间无差异,A和C,B和C之间有差异。 αA αB αC -0.5 -0.3 -0.1 0 0.1 0.3 0.5

第三节加权评分法 一、加权评分法的特点 第一节中所介绍的评分法,没有考虑到食品各项指标的重要程度,从而对产品总的评价 结果造成一定程度的偏差。事实上,对同一种食品,由于各项指标对其质量的影响程度不同, 它们之间的关系不完全是平权的,因此,需要考虑它的权重,所谓加权评分法是考虑各项指 标对质量的权重后求平均分数或总分的方法。加权评分法一般以10分或100分为满分进行 平价。加权平均法比评分法更加客观、公正,因此可以对产品的质量做出更加 作确的评价号 果· 二、权重的确定 所谓权重是指一个因素在被评价因素中的影响和所处的地位。权重的确定是关系到加权 评分法能否顺利实施以及能否得到客观准确的评价结果的关健权重的确 一般是邀请业内 人士根据被评价因素对总体评价结果影响的重要程度,采用德尔菲法进行赋权打分,经统: 获得由各评价因素权重构成的权重集, 通常,要求权重集所有因素a:的总和为1,这称为归一化原则。 设权重集A={a,a,.,a}={a:},(i=1,2,.,n) 则 Sam1 (9-1) 工程技术行业采用常用的“0~4评判法”确定每个因素的权重。一般步骤如下:首先 请若干名(一般8~10人)业内人士对每个因素两两进行重要性比较,根据相对重要性打分: 很重要很不重要,打分4一0:较面要不很重要,打分3一1:同样重要打分2一2。 此得到每个评委对各个因素所打分数表。然后统计所有人的打分,得到每个因素得分,再除 以所有指标总分之和,便得到各因素的权重因子。 例如为获得番茄的颜色、风味、口感、质地这四项指标对保藏后番茄感官质量影响的权 重,邀请10位业内人士对上述四个因素按0一4评判法进行权重打分。统计十张表格各项因 素的得分列于下表。 评委 得分 ABCDEFGHIJ总分 因素 颜色 10939261292971 风味 54105106569868 口感 7697106568468 质地 2 5 2 32623 53 33 合计 24242424242424242424240 将各项因素所得总分除以全部因素总分之和便得权重系数: A=0296.0.283.0.283.0.1381 8
8 第三节 加权评分法 一、加权评分法的特点 第一节中所介绍的评分法,没有考虑到食品各项指标的重要程度,从而对产品总的评价 结果造成一定程度的偏差。事实上,对同一种食品,由于各项指标对其质量的影响程度不同, 它们之间的关系不完全是平权的,因此,需要考虑它的权重,所谓加权评分法是考虑各项指 标对质量的权重后求平均分数或总分的方法。加权评分法一般以 10 分或 100 分为满分进行 评价。加权平均法比评分法更加客观、公正,因此可以对产品的质量做出更加准确的评价结 果。 二、权重的确定 所谓权重是指一个因素在被评价因素中的影响和所处的地位。权重的确定是关系到加权 评分法能否顺利实施以及能否得到客观准确的评价结果的关键。权重的确定一般是邀请业内 人士根据被评价因素对总体评价结果影响的重要程度,采用德尔菲法进行赋权打分,经统计 获得由各评价因素权重构成的权重集。 通常,要求权重集所有因素 ai的总和为 1,这称为归一化原则。 设权重集 A={a1,a2,.,an}={ai},(i=1,2,.,n) 则 1 1 ∑ = = n i ai (9-1) 工程技术行业采用常用的“0~4 评判法”确定每个因素的权重。一般步骤如下:首先 请若干名(一般 8~10 人)业内人士对每个因素两两进行重要性比较,根据相对重要性打分; 很重要~很不重要,打分 4~0;较重要~不很重要,打分 3~1;同样重要,打分 2~2。据 此得到每个评委对各个因素所打分数表。然后统计所有人的打分,得到每个因素得分,再除 以所有指标总分之和,便得到各因素的权重因子。 例如为获得番茄的颜色、风味、口感、质地这四项指标对保藏后番茄感官质量影响的权 重,邀请 10 位业内人士对上述四个因素按 0~4 评判法进行权重打分。统计十张表格各项因 素的得分列于下表。 评委 得分 因素 A B C D E F G H I J 总分 颜色 10 9 3 9 2 6 12 9 2 9 71 风味 5 4 10 5 10 6 5 6 9 8 68 口感 7 6 9 7 10 6 5 6 8 4 68 质地 2 5 2 3 2 6 2 3 5 3 33 合计 24 24 24 24 24 24 24 24 24 24 240 将各项因素所得总分除以全部因素总分之和便得权重系数: A = [0.296, 0.283, 0.283, 0.138]

三、加权评分的结果分析与判断 下式进行。 p=axInf (9-2) 式中:P一总得分: 一评价指标数目 a一各指标的权重: 一评价指标得分 评价指标的满分值。如采用百分制,则户100:如采用十分制,则户10: 如采用五分制,则5, 〔例1):评定茶叶的质量时,以外形权重(20分)、香气与滋味权重(60分入、水色权 重(10分)、叶底权重(10分)作为评定的指标。若评定标准为一级(91~100分)、二级 (81一90分)、三级(71~80分)、四级(61~70分)、五级(5160分).现有一批花茶, 经评审员评审后各项指标的得分数分别为:外形83分:香气与滋味81分:水色82分:叶 底80分 问,该批花茶是几级茶? 解:该批花茶的总分为 83×20)+(81x60)+(82×10)+(80×10=81.4分) 4×100 故该批花茶为二级茶。 第四节模糊数学法 在加权评分法中,仅用一个平均数很难确切的表示某一指标应得的分数,这样使结果存 在误差。如果评定的样品是两个或两个以上,最后的加权平均数出现相同而又需要排列出它 们的各项时,现行的加权评分法就很难解决。如果采用模糊数学关系的方法来处理评定的结 果,以上的问题不仅可以得到解决,而且它综合考虑到所有的因素,获得的是综合且较客观 的结果。模糊数学法是在加权评分法的基础上,应用模糊数学中的模糊关系对食品感官检验 的结果进行综合评判的方法。 一、模糊数学基础知识 模糊综合平判的数学模型是律立在模糊数学基础上的一种定量评价模式。它是应用模期 数学的有关理论(如隶属度与隶属函数理论),对食品感官质量中多因素的制约关系进行数 学化的抽象,建立 个反映其本质特征和动态过程的理想化评价模式。由于我们的评判对 相对简单,评价指标也比较少,食品感官质量的模糊评判常采用一级模型。模糊评判所应用 的模糊数学的基础知识,主要为以下内容: (1)建立评判对象的因素集={u1,2,.,u,}。因素就是对象的各种属性或性能」 例如评价蔬菜的感官质量,就可以选择蔬菜的颜色、风味、口感、质地作为考虑的因素。因 此,评判因素可设山=颜色:=风味:=口感:山质地:组成评判因素集合是 U={U1,u2,u1}. (2)给出评语集V: V=(V,V2,.,V}a
9 三、加权评分的结果分析与判断 该方法的分析及判断方法比较简单,就是对各评价指标的评分进行加权处理后,求平均 得分或求总分的办法,最后根据得分情况来判断产品质量的优劣。加权处理及得分计算可按 下式进行。 p a x nf n i i i / 1 ∑ = = (9-2) 式中:P——总得分; n——评价指标数目; a——各指标的权重; x——评价指标得分; f——评价指标的满分值。如采用百分制,则 f=100;如采用十分制,则 f=10; 如采用五分制,则 f=5。 〔例 1〕:评定茶叶的质量时,以外形权重(20 分)、香气与滋味权重(60 分)、水色权 重(10 分)、叶底权重(10 分)作为评定的指标。若评定标准为一级(91~100 分)、二级 (81~90 分)、三级(71~80 分)、四级(61~70 分)、五级(51~60 分)。现有一批花茶, 经评审员评审后各项指标的得分数分别为:外形 83 分;香气与滋味 81 分;水色 82 分;叶 底 80 分。问,该批花茶是几级茶? 解:该批花茶的总分为 81.4(分) 4 100 (83 20) (81 60) (82 10) (80 10) = × × + × + × + × 故该批花茶为二级茶。 第四节 模糊数学法 在加权评分法中,仅用一个平均数很难确切的表示某一指标应得的分数,这样使结果存 在误差。如果评定的样品是两个或两个以上,最后的加权平均数出现相同而又需要排列出它 们的各项时,现行的加权评分法就很难解决。如果采用模糊数学关系的方法来处理评定的结 果,以上的问题不仅可以得到解决,而且它综合考虑到所有的因素,获得的是综合且较客观 的结果。模糊数学法是在加权评分法的基础上,应用模糊数学中的模糊关系对食品感官检验 的结果进行综合评判的方法。 一、模糊数学基础知识 模糊综合评判的数学模型是建立在模糊数学基础上的一种定量评价模式。它是应用模糊 数学的有关理论(如隶属度与隶属函数理论),对食品感官质量中多因素的制约关系进行数 学化的抽象,建立一个反映其本质特征和动态过程的理想化评价模式。由于我们的评判对象 相对简单,评价指标也比较少,食品感官质量的模糊评判常采用一级模型。模糊评判所应用 的模糊数学的基础知识,主要为以下内容: (1)建立评判对象的因素集 U={u1,u2,.,un}。因素就是对象的各种属性或性能。 例如评价蔬菜的感官质量,就可以选择蔬菜的颜色、风味、口感、质地作为考虑的因素。因 此,评判因素可设 u1=颜色;u2=风味;u3=口感;u4=质地;组成评判因素集合是: U={u1,u2,u3,u4}。 (2)给出评语集 V: V={V1,V2,.,Vn}

评语集由若干个最能反映该食品质量的指标组成,可以用文字表示,也可用数值或等级 表示 如保藏后蔬菜样品的感官质量划分为四个等级,可设: V=中:V 则 V=(VI,V2,Va,V. (3)建立权重集 确定各评判因素的权重集X,所谓权重是指一个因素在被评价因素中的影响和所处的地 位。其确定方法与前面加权评分法中介绍的方法相同。 (4)建立单因素评判 对每一个被评价的因素建立一个从U到V的模糊关系R,从而得出单因素的评价集:矩 阵R可以通过对单因素的评判获得,即从U:若眼而得到单因素评判,构成R中的第i行。 ru re A r R= rA r. L'at A 即:R=(r)i=1,2,n:j=1,2,m。这里的元素r表示从因素山:到该因 素的评判结果V,的隶属程度。 (5)综合评判 求出R与X后,进行模糊变换 B=X·R={b1,b2,.,bn (9-3) X·R为矩阵合成,矩阵合成运算按照最大隶属度原则。再对B进行归一化处理得到B B'=b, B便是该组人员对高食品感官质最的评语集。最后,再由最大隶属原则确定该种食品 感官质量的所属评语。 二、模糊数学评价方法。 根据模糊数学的基本理论,模糊评判实施主要有:因素集、评语集、权重、模糊矩阵、 模糊变换、模糊评价等部分组成。下面结合实例来介绍模糊数学评价法的具体实施过程。 (例1):设花茶的因素集为U: U=外形u,香气与滋味u,水色u,叶底u:}。 评语集为V V={一级、二级、三级、四级、五级} 其中一级(91~100分),二级(81~90分),三级(71~80分),四级(61一70分),五级 (51-60分)。 设权重集为X X={0.2,0.6,0.10.1} 即外形20分,香气与滋味60分,水色10分,叶底10分,共计100分。 10名评价员(k=10),对花茶各项指标的评分如下表所示。 问该花茶为几级茶?
10 评语集由若干个最能反映该食品质量的指标组成,可以用文字表示,也可用数值或等级 表示。 如保藏后蔬菜样品的感官质量划分为四个等级,可设: V1=优;V2=良;V 3=中;V 4=差 则 V={V1,V2,V3,V4}。 (3)建立权重集 确定各评判因素的权重集 X,所谓权重是指一个因素在被评价因素中的影响和所处的地 位。其确定方法与前面加权评分法中介绍的方法相同。 (4)建立单因素评判 对每一个被评价的因素建立一个从 U 到 V 的模糊关系 R,从而得出单因素的评价集;矩 阵 R 可以通过对单因素的评判获得,即从 Ui着眼而得到单因素评判,构成 R 中的第 i 行。 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = m m mn n n r r r r r r r r r R Λ Μ Μ Μ Λ Λ 1 2 21 22 2 11 12 1 即:R=(rij)i=1,2,.,n;j=1,2,.,m。这里的元素 rij表示从因素 ui到该因 素的评判结果 Vj的隶属程度。 (5)综合评判 求出 R 与 X 后,进行模糊变换: B=X·R={b1,b2,.,bm} (9-3) X·R 为矩阵合成,矩阵合成运算按照最大隶属度原则。再对 B 进行归一化处理得到 B ′ B′={b1′,b2′,.,bm′} B′便是该组人员对高食品感官质量的评语集。最后,再由最大隶属原则确定该种食品 感官质量的所属评语。 二、模糊数学评价方法。 根据模糊数学的基本理论,模糊评判实施主要有:因素集、评语集、权重、模糊矩阵、 模糊变换、模糊评价等部分组成。下面结合实例来介绍模糊数学评价法的具体实施过程。 〔例 1〕:设花茶的因素集为 U。 U={ } 外形u1 ,香气与滋味u2,水色u3 ,叶底u4 。 评语集为 V V={ } 一级、二级、三级、四级、五级 其中一级(91~100 分),二级(81~90 分),三级(71~80 分),四级(61~70 分),五级 (51~60 分)。 设权重集为 X X={ } 0.2 ,0.6 ,0.1 ,0.1 即外形 20 分,香气与滋味 60 分,水色 10 分,叶底 10 分,共计 100 分。 10 名评价员(k=10),对花茶各项指标的评分如下表所示。 问该花茶为几级茶?