
第十六章实验方法评价与数据处理 第一节实验方法评价 随着食品科学的不断发展,食品检验方法不断更新,评价检验方法的标准也逐步建立和 完善起来。这些评价标准主要是准确度、精密度、检测限以及费用与效益。 一.评价指标 1、准确府 准确度是指在一定条件下,多次测定的平均值与真实值相符合的程度。准确度通常用绝 对误差或相对误差表示。 在实际工作中,一般在试样中添加己知标准物质量作为真值,并以回收率表示准确度。 即: P%=X-Xx100% 16-1 m 式中:P(%) 一加入标准物质的回收率: X,一加标样品测定值 X 一试样本底测定值 —加入标准物质的质量 式中的本底值X0,其测定精密度所显示误差是反映随机误差:加入标准物质的质量m 其测定误差反映了系统误差。所以,回收率是两种误差综合指标,能决定方法的可靠性。 对回收率的要求数值是个比较复杂的问题,依分析测定方法难易和不同类型的分析方法而 变化。一般ppm级应在90%以上:Ppb级如荧光法测定苯并花在80%:比较繁杂的方法70% 即可:但最低不能小于70%。 2、精密度 精密度是指多次重复测定某一样品时,所得测定值的离散程度。精密度通常用标准差或 相对标准差来表示。 重复测定的精密度与待测物质绝对量有关,一般规定:mg级Cv(变异系数或相对标准 狗级C为10呢级为0左右 检测限是指分析方法在适当的置信水平内,能从样品检测被测组分的最小量或最小浓 度,即断定样品中被测组分的量或浓度确实高于空白中被测组分的最低量。 一般对检测限有几种规定方法: (1)气相色谱法:用最小检测量或最小检测浓度表示 最小检测量是指检测器恰能产生色谱峰高大于二倍噪音时的最小进样最。即: S-2N 163 式中:S最小响应值 N噪音信号 最小检测浓度是指最小检测量与进样量体积之比。即单位进样量相当待测物质的量。 例16-1用气相色谱法测定聚氯乙烯成型品中氯乙烯单体的检测限。仪器噪音的最大信 号为峰高1.0mm,注入0.5ug氯乙烯标准制备的顶空气3ml,响应值为12mm,求最低检测 题解:根据公式[16-21S=2N=2×1.0mm=2.0mm
第十六章 实验方法评价与数据处理 第一节 实验方法评价 随着食品科学的不断发展,食品检验方法不断更新,评价检验方法的标准也逐步建立和 完善起来。这些评价标准主要是准确度、精密度、检测限以及费用与效益。 一.评价指标 1、准确度 准确度是指在一定条件下,多次测定的平均值与真实值相符合的程度。准确度通常用绝 对误差或相对误差表示。 在实际工作中,一般在试样中添加已知标准物质量作为真值,并以回收率表示准确度。 即: 16-1 式中:P(%)——加入标准物质的回收率; X1——加标样品测定值 X0——试样本底测定值 m——加入标准物质的质量 式中的本底值 Xo,其测定精密度所显示误差是反映随机误差;加入标准物质的质量 m, 其测定误差反映了系统误差。所以,回收率是两种误差综合指标,能决定方法的可靠性。 对回收率的要 求数值是个比较复杂的问题,依分析测定方法难易和不同类型的分析方法而 变化。一般 ppm 级应在 90%以上;ppb 级如荧光法测定苯并芘在 80%;比较繁杂的方法 70% 即可;但最低不能小于 70%。 2、精密度 精密度是指多次重复测定某一样品时,所得测定值的离散程度。精密度通常用标准差或 相对标准差来表示。 重复测定的精密度与待测物质绝对量有关,一般规定:mg 级 Cv(变异系数或相对标准 差)为 5%;μg 级 Cv 为 10%,ng 级 Cv 为 50%左右。 3、检测限 检测限是指分析方法在适当的置信水平内,能从样品检测被测组分的最小量或最小浓 度,即断定样品中被测组分的量或浓度确实高于空白中被测组分的最低量。 一般对检测限有几种规定方法: (1)气相色谱法:用最小检测量或最小检测浓度表示 最小检测量是指检测器恰能产生色谱峰高大于二倍噪音时的最小进样量。即: S=2N 16-2 式中:S-最小响应值 N-噪音信号 最小检测浓度是指最小检测量与进样量体积之比。即单位进样量相当待测物质的量。 例 16-1 用气相色谱法测定聚氯乙烯成型品中氯乙烯单体的检测限。仪器噪音的最大信 号为峰高 1.0mm,注入 0.5ug 氯乙烯标准制备的顶空气 3ml,响应值为 12mm,求最低检测 量? 题解:根据公式[16-2] S=2N=2×1.0mm=2.0mm (%) 1 0 ×100% − = m X X P

最小检测量 注入标准物质量 可知道 最小响应值 标准物质的响应值 最小检测量=最小响应值×注入标准物质量-2X052=083e 标准物质的响应值 例16-2在上例中,如果注入3ml顶空气相当于0.5g聚氯乙烯成型品,求最小检测浓度? 题解:最小检测浓度-0.083/0.5=0.17ugg (2)吸光光度法 在吸光光度法中,扣除空白值后,吸光值为0.01所对应的浓度做为检测限。 例163利用镉离子与6溴苯并噻唑偶氨萘酚形成红色络合物,对食品中镉含量进行比 色测定。对全试剂空白进行5次平行测定,吸光度平均值是0.003,再测定0.25g标准镉溶 液,其吸光度为0.023,求检测限? 检测限 锅标准质量 题解:由最小响应值=镉标准吸光度一空白吸光度可以知道: 最小响应值×幅标准质量 检测限= 镉标准吸光度-空白吸光度=0.01×0.25/0.023-0.003=0.125ug (3)一般实验:当空白测定次数N>20时,给出置信水平95%,检测限为空白值正标 准差(S)的4.6倍。即:检测限=4.6× 16-3 例16-4在例16-3中,当空白测定N>20时,吸光度0.003士0.001相当于镉0.0375± 0.01 g求检测限? 题解:按式[16-3]检测限=4.6×S=4.6×0.013-0.06g 若空白测定次数n<20时,检测限按下式计算 检测限=2√21,S 16-4 式中:t置信水平为95%(单侧),批内自由度为f时的临界值 批内自由度 与m(n-l),m为重复测定次数, n为平行测定次数。 例16-5用2、3一二氨基萘荧光法测定硒,双空白测定10次,其空白值为11.4士1.3g, 求检测限? 题解:根据=m(n-1=10*2.1=10 查附表,当置信水平95%(单侧)时,10223 按式16-4小,检测限=221,S=2×1.414×223×1.3=8.20ng (4)国际理论应用化学联合会对检测限的规定 对于各种光学分析方法,可测量的最小分析响应值以下式表示 XL=。-K×S。 16-5 式中:X-最小响应值 。-多次测量空白值的平均值(n≥20) S。-多次测量空白值的标准差:
由 = 可知道 =2×0.5/12=0.083ug 例 16-2 在上例中,如果注入 3ml 顶空气相当于 0.5g 聚氯乙烯成型品,求最小检测浓度? 题解:最小检测浓度=0.083/0.5=0.17μg/g (2)吸光光度法 在吸光光度法中,扣除空白值后,吸光值为 0.01 所对应的浓度做为检测限。 例 16-3 利用镉离子与 6-溴苯并噻唑偶氮萘酚形成红色络合物,对食品中镉含量进行比 色测定。对全试剂空白进行 5 次平行测定,吸光度平均值是 0.003,再测定 0.25μg 标准镉溶 液,其吸光度为 0.023,求检测限? 题解: 由 最小响应值 检测限 = 镉标准吸光度 空白吸光度 镉标准质量 − 可以知道: 镉标准吸光度 空白吸光度 最小响应值 镉标准质量 检测限 − × = =0.01×0.25/0.023-0.003=0.125ug (3)一般实验:当空白测定次数 N>20 时,给出置信水平 95%,检测限为空白值正标 准差(S)的 4.6 倍。即:检测限=4.6×S 16-3 例 16-4 在例 16-3 中,当空白测定 N>20 时,吸光度 0.003±0.001 相当于镉 0.0375± 0.013μg 求检测限? 题解:按式[16-3]检测限=4.6×S=4.6×0.013=0.06μg 若空白测定次数 n<20 时,检测限按下式计算 t Sf 检测限 = 2 2 16-4 式中;tf-置信水平为 95%(单侧),批内自由度为 f 时的临界值 f-批内自由度 f=m(n-1),m 为重复测定次数, n 为平行测定次数。 例 16-5 用 2、3 一二氨基萘荧光法测定硒,双空白测定 10 次,其空白值为 11.4±1.3ng, 求检测限? 题解:根据 f=m(n-1)=10*(2-1)=10 查附表,当置信水平 95%(单侧)时,t10=2.23 按式[16-4], =2×1.414×2.23×1.3=8.20ng (4)国际理论应用化学联合会对检测限的规定 对于各种光学分析方法,可测量的最小分析响应值以下式表示 X L = Xb − K × Sb 16-5 式中:XL-最小响应值; Xb − 多次测量空白值的平均值(n≥20); Sb- 多次测量空白值的标准差; 检测限 = 2 2t f S 最小响应值 最小检测量 标准物质的响应值 注入标准物质量 标准物质的响应值 最小响应值 注入标准物质量 最小检测量 × =

K-根据一定置信水平确定的系数(一般当置信水平为90%,空白测量次数20时,K=4.65). 规定,检测限=七足。K×S 16-.6 式中,m为方法灵敏度,即单位浓度或单位量被则物质所产生的响应值的变化程度,在实际 工作中,以标准曲线斜率度量灵敏度,基余各项符号同式[165]。 例166在例16.5测定西时,物加空白则定数,比空白俏为:101+095ng,其灵敏府 为0.54荧光单位e,求检测限 题解:按16-6 检测限=-无-K×S =3×0.95/0.54=528ng m 从检测限定义可以知道,增加实际测定次数,提高测定精密度,降低仪器噪音,可以改 善检测限。 4、费用与效益 费用与效益是目前国内外重视的问题。实验室工作人员,应结合实际测试目标,选择或 设计相应准确度和精密度的实验方法。用一般常规实验能够完成的测定,不必使用贵重精密 仪器。检验员经训练能较好堂据某种测定方法的时间,也是评价实验方法的重要内容。“简 单易学”在一定程度上意味着能保证检验质量。从实际工作需要出发,快速,微量,费用低 技术要求不高,操作安全的测定方法应列为一般实验室的首选方法 ,实验结果的检验 在食品分析中,常遇到两个平均值的比较问题,如测定平均值和己知值的比较,不同分 析人员,不同实验室,或用不同分析方法测定的平均值的比较,对比性试验研究等均属于此 类问题。所以对这类问题常采用显著性检验法利用统计方法来检验被处理问题是否存 在统计上的显若性,常用有1检验法和F检验法 1、t检验法 用以比较一个平均值与标准值之间或两个平均值之间是否有在显著性差异。 进行t检验的程序如下: (1)选定所用的检验统计量: 当检验样本均值下与总体均值μ是否有显著性差异时,使用统计量 灭-4 16-7 式中:、一标准差 当检验两个均值之间是否有显著性差异时,使用统计量 n1×n2 Vm+nz 16-8 其中S合并标准差 按下式计算: 5= -1)S+(n2-10S n1+n2-2 16-9
K-根据一定置信水平确定的系数(一般当置信水平为 90%,空白测量次数 n<20 时,K=3; 置信水平为 95%,n>20 时,K=4.65)。 规定: m K S m X L Xb × b = − 检测限 = 16-6 式中,m 为方法灵敏度,即单位浓度或单位量被则物质所产生的响应值的变化程度,在实际 工作中,以标准曲线斜率度量灵敏度,基余各项符号同式[16-5]。 例 16-6 在例 16-5 测定硒时,增加空白测定数,其空白值为:10.1±0.95ng,其灵敏度 为 0.54 荧光单位/ng,求检测限? 题解:按 16-6 式 =3×0.95/0.54=5.28ng 从检测限定义可以知道,增加实际测定次数,提高测定精密度,降低仪器噪音,可以改 善检测限。 4、费用与效益 费用与效益是目前国内外重视的问题。实验室工作人员,应结合实际测试目标,选择或 设计相应准确度和精密度的实验方法。用一般常规实验能够完成的测定,不必使用贵重精密 仪器。检验员经训练能较好掌握某种测定方法的时间,也是评价实验方法的重要内容。“简 单易学”在一定程度上意味着能保证检验质量。从实际工作需要出发,快速,微量,费用低 廉,技术要求不高,操作安全的测定方法应列为一般实验室的首选方法。 二.实验结果的检验 在食品分析中,常遇到两个平均值的比较问题,如测定平均值和已知值的比较,不同分 析人员,不同实验室,或用不同分析方法测定的平均值的比较,对比性试验研究等均属于此 类问题。所以对这类问题常采用显著性检验法-利用统计方法来检验被处理问题是否存 在统计上的显著性,常用有 t 检验法和 F 检验法。 1、t 检验法 用以比较一个平均值与标准值之间或两个平均值之间是否有在显著性差异。 进行 t 检验的程序如下: (1)选定所用的检验统计量: 当检验样本均值 X 与总体均值 μ 是否有显著性差异时,使用统计量 S n X t / − μ = 16—7 式中:S—标准差 当检验两个均值之间是否有显著性差异时,使用统计量 1 2 1 2 1 2 n n n n S X X t + × × − = 16—8 其中 S -合并标准差 按下式计算: 2 ( 1) ( 1) 1 2 2 2 2 2 1 1 + − − + − = n n n S n S S 16—9 m K S m XL Xb × b = − 检测限 =

式中S第一个样本的方差 S第二个样本的方差 n4一第一个样本的测定次数 2一第二个样本的测定次数 (2)计算统计量, 如果由样本值计算的统计量值大于t分布表中相应显著性水平α和相应自由度f下的临 界值。则表明被检验的均值有显若性差异,反之,差异不显若。 应用↑检验时,垫求被检险的两组数据具有相同或相近的方差(标准差)。因此在↑检 验之前必须进行F检验,只有在两方差一致性前提下才能进行t检验。 (3)假设检验的一尾测验与两尾测验 在进行测验结果分析确定检验水平时,还应根据其处理的性质和试验结果的准确性,考 虑显著性测验用 尼测验还是用两尾测 在提出一个统计假设时,必然有一个与其相对应的备择假设。备择假设为否定假设时, 必然接受的另一个假设。例如,单个平均数进行显著性测验时,通常H0:u一o,H:μ≠o。 如果H被否定接受H时,其μ≠,便有μ大于或小于的两种可能性,即所测定的 误差概率在正态分布曲线的左尾和右尾各有一个否定域,而附表中临界值表规定的。 值是两尾概率之 ,如果确定的检验水平a-0.05,则两尾否定域的概率各为0.025,这类测 验称这为两尾测验 但有的试验则不然,例如某酿酒厂曲种酿造醋的醋酸含量大于12%,则其假设H:“ >12%,H:μ≤12%。如果选择的曲种粮造醋酸含量大于12%,H6被否定,μ只能大于12%。 若小于12%。便不符合规定的企业标准,没有推广价值,因此只有在正态曲线的右尾一个否 定域,这类检验称为一尾测验。两尾测验查两尾概表或一尾测验查 尾概率表时,可以直接 从表上查得。如果两尾检验查一尾概表时,需将检验水平值除 再查出。值,如两尾测 验检验水平a=0.05,一尾概率00s=1.64,应将检验水平=0.05除以2得=0.025,0ms=224, 如果一尾检验查两尾概率表时需将检验水平值乘以2,再查出值,如一尾检验水平a=0.1, o=1.64,因此用一尾测验还是用两尾测验,应认真从实际考虑。 而1检验法为判别性测验,多为两尾测验。 下面将t检验法在食品分析中的主要应用介绍如下 ①用已知组成的标样评价分析方法 为了鉴定一个分析方法的可靠性,可用一已知量的基准物或已知含量的标准试样进行对 照试验,通过若干次测定,取得其平均值,然后将这个平均值与已知值(真值)进行比较, 从而制断这个分析方法是否存在系统误差。因为这时将平均值与真值进行比较,所以可以按 t检验法来判别。 逻辑推理是先假设平均值与真值之间不存在真正的差异, 如果所算出的 值大于通常规定的置信水平的t值,那么,应该拒绝所提的假设,就是说,这样的差异不 认为是偶然的误差,而是被检验的方法存在系统误差,反之,则应接该受假设,判断该方法 不存在系统误差, 例16-7为了鉴定一个分析方法的准确度,取重量为100mg的基准物进行10次测定, 所得数据为100.3,992,99.4,100.0,99.7,99.9,99.4,100.1,99.4,99.6,试对这组数据 进行评价。 题解:计算平均值和标准偏差。X=99.7,S=0.38,按式16-7,计算统计量
式中 2 S1 -第一个样本的方差 2 S2 -第二个样本的方差 n1-第一个样本的测定次数 n2-第二个样本的测定次数 (2)计算统计量, 如果由样本值计算的统计量值大于 t 分布表中相应显著性水平 α 和相应自由度 f 下的临 界值 tα, f,则表明 被检验的均值有显著性差异,反之,差异不显著。 应用 t 检验时,要求被检验的两组数据具有相同或相近的方差(标准差)。因此在 t 检 验之前必须进行 F 检验,只有在两方差一致性前提下才能进行 t 检验。 (3)假设检验的一尾测验与两尾测验 在进行测验结果分析确定检验水平时,还应根据其处理的性质和试验结果的准确性,考 虑显著性测验用一尾测验还是用两尾测验。 在提出一个统计假设时,必然有一个与其相对应的备择假设。备择假设为否定假设时, 必然接受的另一个假设。例如,单个平均数进行显著性测验时,通常 H0:μ=μ0,HA:μ≠μ0。 如果 H0 被否定接受 HA时,其 μ≠μ0,便有 μ 大于 μ0或小于 μ0的两种可能性,即所测定的 误差概率在正态分布曲线的左尾和右尾各有一个否定域,而附表_1_中临界 t 值表规定的 α 值是两尾概率之和。如果确定的检验水平 α=0.05,则两尾否定域的概率各为 0.025,这类测 验称这为两尾测验。 但有的试验则不然,例如某酿酒厂曲种酿造醋的醋酸含量大于 12%,则其假设 H0:μ >12%,HA:μ≤12%。如果选择的曲种酿造醋酸含量大于 12%,H0 被否定,μ 只能大于 12%。 若小于 12%便不符合规定的企业标准,没有推广价值,因此只有在正态曲线的右尾一个否 定域,这类检验称为一尾测验。两尾测验查两尾概表或一尾测验查一尾概率表时,可以直接 从表上查得。如果两尾检验查一尾概表时,需将检验水平值除 2,再查出 µα 值,如两尾测 验检验水平 α=0.05,一尾概率 µ0.05=1.64,应将检验水平 α=0.05 除以 2 得 α=0.025,µ0.025=2.24, 如果一尾检验查两尾概率表时需将检验水平值乘以 2,再查出 µα值,如一尾检验水平 α=0.1, µ0.1=1.64,因此用一尾测验还是用两尾测验,应认真从实际考虑。 而 t 检验法为判别性测验,多为两尾测验。 下面将 t 检验法在食品分析中的主要应用介绍如下: ①用已知组成的标样评价分析方法 为了鉴定一个分析方法的可靠性,可用一已知量的基准物或已知含量的标准试样进行对 照试验,通过若干次测定,取得其平均值,然后将这个平均值与已知值(真值)进行比较, 从而制断这个分析方法是否存在系统误差。因为这时将平均值与真值进行比较,所以可以按 t 检验法来判别。逻辑推理是先假设平均值与真值之间不存在真正的差异,如果所算出的 t 值大于通常规定的置信水平的 t 值,那么,应该拒绝所提的假设,就是说,这样的差异不能 认为是偶然的误差,而是被检验的方法存在系统误差,反之,则应接该受假设,判断该方法 不存在系统误差。 例 16-7 为了鉴定一个分析方法的准确度,取重量为 100mg 的基准物进行 10 次测定, 所得数据为 100.3,99.2,99.4,100.0,99.7,99.9,99.4,100.1,99.4,99.6,试对这组数据 进行评价。 题解:计算平均值和标准偏差。 X =99.7,S=0.38,按式 16—7,计算统计量
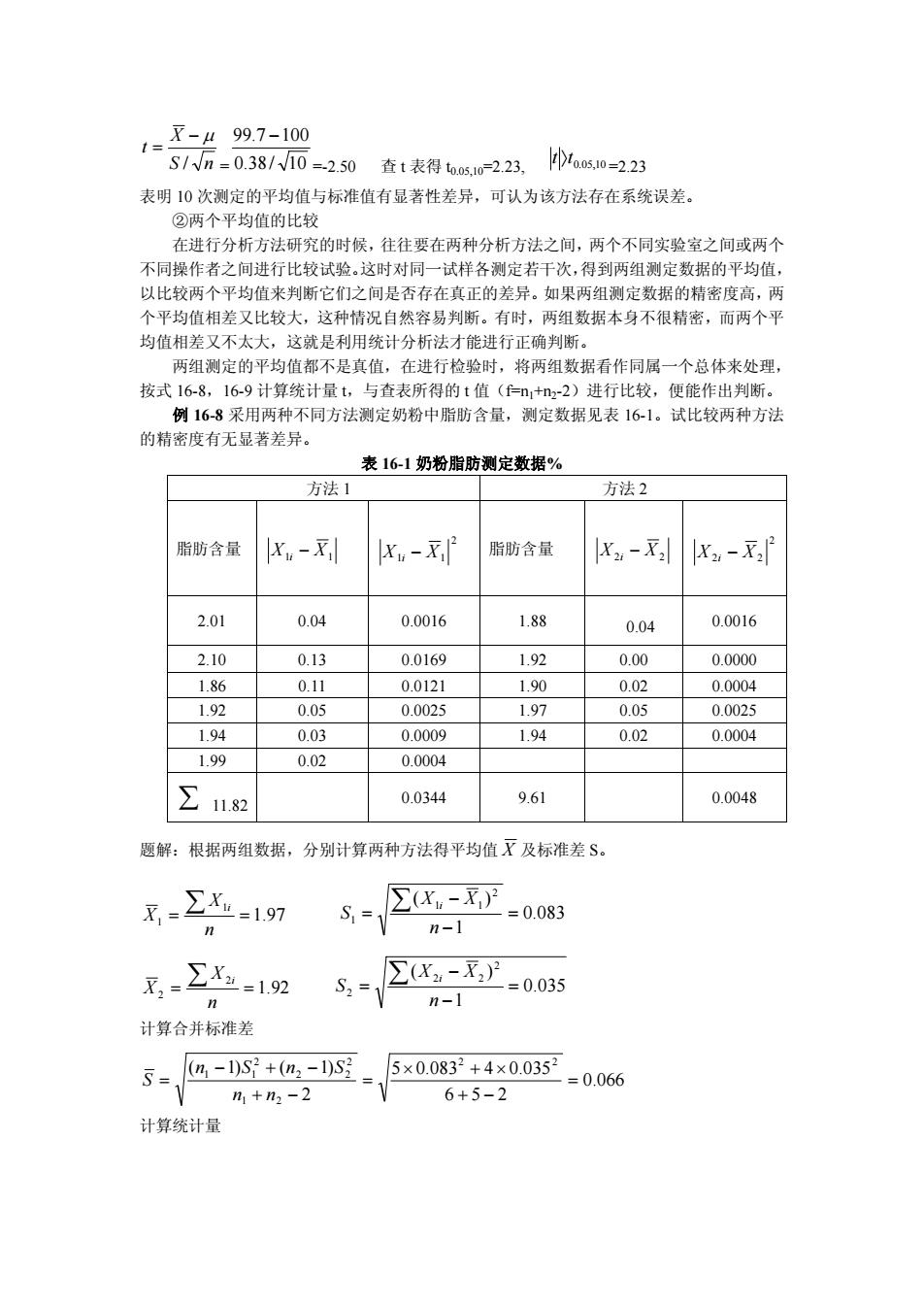
1=X-497-10 S1.0.38/而=-250查1表得6w223.ps0=223 表明10次测定的平均值与标准值有显著性差异,可认为该方法存在系统误差 ②两个平均值的比较 在进行分析方法研究的时候,往往要在两种分析方法之间,两个不同实验室之间或两个 不同操作者之间进行比较试验。这时对同一试样各测定若干次,得到两组测定数据的平均值, 以出较两个平均值来判断它们之间是否存在直正的差异。加里两组删定数据的持密度高。两 个平均值相差又比较大, 这种情况自然容易判断。有时,两组数据本身不很精密,而两个平 均值相差又不太大,这就是利用统计分析法才能进行正确判断。 两组测定的平均值都不是真值,在进行检验时,将两组数据看作同属一个总体来处理, 按式16-8,16-9计算统计量t,与查表所得的t值(f=n+m2-2)进行比较,便能作出判断。 例16-8采用两种不同方法测定奶粉中脂肪含量,测定数据见表16-1。试比较两种方法 的精密度有无显著差异。 表161奶粉脂肪测定数据% 方法1 方法2 脂肪含量 Xv-X x-Xl 脂肪含量 X-X2x2-X2 2.01 0.04 0.0016 1.88 0.04 0.0016 210 0.13 0.0169 1.92 000 00000 1.86 0.11 0.0121 1.90 0.02 0.0004 1.92 0.05 0.0025 1.97 0.05 0.0025 194 003 00009 1.94 0.02 0.0004 1g0 0.02 0.0004 ∑182 0.0344 9.61 0.0048 题解:根据两组数据,分别计算两种方法得平均值灭及标准差$。 X=∑X=197 S,= ∑(Xw-x)7 =0.083 n-1 ,=X-192 ∑(X-x2) =0.035 n- 计算合并标准差 5=4-0s+a,-sg 5×0.0832+4×0.0352 =0.066 m+n2-2 6+5-2 计算统计量
S n X t / − μ = = 0.38/ 10 99.7 −100 =-2.50 查 t 表得 t0.05,10=2.23, 0.05,10 t 〉t =2.23 表明 10 次测定的平均值与标准值有显著性差异,可认为该方法存在系统误差。 ②两个平均值的比较 在进行分析方法研究的时候,往往要在两种分析方法之间,两个不同实验室之间或两个 不同操作者之间进行比较试验。这时对同一试样各测定若干次,得到两组测定数据的平均值, 以比较两个平均值来判断它们之间是否存在真正的差异。如果两组测定数据的精密度高,两 个平均值相差又比较大,这种情况自然容易判断。有时,两组数据本身不很精密,而两个平 均值相差又不太大,这就是利用统计分析法才能进行正确判断。 两组测定的平均值都不是真值,在进行检验时,将两组数据看作同属一个总体来处理, 按式 16-8,16-9 计算统计量 t,与查表所得的 t 值(f=n1+n2-2)进行比较,便能作出判断。 例 16-8 采用两种不同方法测定奶粉中脂肪含量,测定数据见表 16-1。试比较两种方法 的精密度有无显著差异。 表 16-1 奶粉脂肪测定数据% 方法 1 方法 2 脂肪含量 X1i − X1 2 X1i − X1 脂肪含量 X 2i − X 2 2 X 2i − X 2 2.01 0.04 0.0016 1.88 0.04 0.0016 2.10 0.13 0.0169 1.92 0.00 0.0000 1.86 0.11 0.0121 1.90 0.02 0.0004 1.92 0.05 0.0025 1.97 0.05 0.0025 1.94 0.03 0.0009 1.94 0.02 0.0004 1.99 0.02 0.0004 ∑ 11.82 0.0344 9.61 0.0048 题解:根据两组数据,分别计算两种方法得平均值 X 及标准差 S。 1.97 1 1 = = ∑ n X X i 0.083 1 ( ) 2 1 1 1 = − − = ∑ n X X S i 1.92 2 2 = = ∑ n X X i 0.035 1 ( ) 2 2 2 2 = − − = ∑ n X X S i 计算合并标准差 0.066 6 5 2 5 0.083 4 0.035 2 ( 1) ( 1) 2 2 1 2 2 2 2 2 1 1 = + − × + × = + − − + − = n n n S n S S 计算统计量

1-n4-197-125x6=1383 5Vm+m20.066V5+6 查t表得【005y22622,t<t05两法差别不显著,即两种测定结果是一致的。 ③酒配对比较试验数据 在分析方法试验中,为了判断某一个因素的结果否有显若影响,往往取若干批的试样, 将其他因素固定下来,对某一因素进行配对的比较试验。这样的试验可以消除其它因素的影 响而把被检验的因素突出来,以便从随机误差的覆盖下找出被检验的因素是否存在真正的 差异。例如为了比较两个实验室的分析结果,取若干批试样交由两个实验室进行比较测定 为了比较两种分析方法的差异性,可以用两种不同方法对同一试样进行测定比较也可以把 个试样交给几个人进行方法的比较试验等等。 配对比较试验数据的判断,不是根据两组数据的平均值来进比较,而是根据各组配对数 据之差D来进行显著性的检验。 首先计算配对数据之差D的平均值万,标准差SD D=∑D 16-10 ∑(D,-D)2 ∑D-①D)☑ S。= n-1 n-1 16-11 然后计算统计量t SD 16-12 如果计算的统计量值小于t分布表中相不在显著性水平α和相应自由度f的临界值t 则表明被检验的两种方法测定结果是一致的。 例169某实哈室使用吉接离子计测定饮料中的每含量。为了检验新方法的可靠性,用 新法和老法(氟试剂比色法)同时对10份不同饮料进行了对比性测定,结果见表16-2,两 法的测定结果是否一致? 表16-2两种方法测定氟含量数据 氧金最(m几) 相差值D, D 饮料样品 氟试剂比色法直接离子计法 4.18 4.4 -0.24 0.0576 4.04 4.17 -013 0.0169 436 314 122 14884 3.01 2.94 007 0.0049 1.66 1.20 0.46 0.2116 6 1031 7.96 2.35 5.5225 7 502 980 -388 150544 8 25 143 1.07 1.1449 9 5.98 3.97 2.01 4.0401 10 6.56 4.83 1.73 2.9929
1.383 5 6 5 6 0.066 1.97 1.92 1 2 1 2 1 2 = + − × = + − = n n n n S X X t 查 t 表得 t 0.05,9=2.2622, t<t 0.05,9, 两法差别不显著,即两种测定结果是一致的。 ③配对比较试验数据 在分析方法试验中,为了判断某一个因素的结果否有显著影响,往往取若干批的试样, 将其他因素固定下来,对某一因素进行配对的比较试验。这样的试验可以消除其它因素的影 响而把被检验的因素突出来,以便 从随机误差的覆盖下找出被检验的因素是否存在真正的 差异。例如为了比较两个实验室的分析结果,取若干批试样交由两个实验室进行比较测定; 为了比较两种分析方法的差异性,可以用两种不同方法对同一试样进行测定比较也可以把一 个试样交给几个人进行方法的比较试验等等。 配对比较试验数据的判断,不是根据两组数据的平均值来进比较,而是根据各组配对数 据之差 D 来进行显著性的检验。 首先计算配对数据之差 D 的平均值 D ,标准差 SD 16—10 1 ( ) 1 ( ) 2 2 2 − − = − − = ∑ ∑ ∑ n n D D n D D S i i i D 16—11 然后计算统计量 t D D S D n t × = 16-12 如果计算的统计量值小于 t 分布表中相不在显著性水平 α 和相应自由度 f 的临界值 t α,f, 则表明被检验的两种方法测定结果是一致的。 例 16-9 某实验室使用直接离子计测定饮料中的氟含量 。为了检验新方法的可靠性,用 新法和老法(氟试剂比色法)同时对 10 份不同饮料进行了对比性测定,结果见表 16-2,两 法的测定结果是否一致? 表 16-2 两种方法测定氟含量数据 氟含量(mg/L) 相差值 Di Di 2 饮料样品 氟试剂比色法 直接离子计法 1 4.18 4.42 -0.24 0.0576 2 4.04 4.17 -0.13 0.0169 3 4.36 3.14 1.22 1.4884 4 3.01 2.94 0.07 0.0049 5 1.66 1.20 0.46 0.2116 6 10.31 7.96 2.35 5.5225 7 5.92 9.80 -3.88 15.0544 8 2.5 1.43 1.07 1.1449 9 5.98 3.97 2.01 4.0401 10 6.56 4.83 1.73 2.9929 n D D ∑ i =

4.66 30.5342 题解:按式16一10,16-11计算差数的平均值万与标准差S。 D、∑D n=4.66/10=0.466mg/1 ∑(D,-D ∑p②D)P7 S。=n-1 n-1 =1.78mg/ n-Dx0466x10 按式16一12计算t值 S。=1.78 =-0.83 查t分布表,当=9时,t0s,-2.26,tfa(,)时,则两组方差之间有显著性差异,反之,则两组方差无显著性 差异。 在编制F分布表时,是将大方差作分子,小方差作分母,所以,在由样本值计算统计 量F值时,也要将样本方差S,S中数值较大的一个作分子,较小的一个作分母。 例16-10仍以例16-8中实验数据为例,通过F检验法比较两种方法的精密度有无显著 差异。 顺解:分别计算两种方法的方差 S2-0.0832-0.0069 2-0032001 按式16-13计算统计量方差比F:
∑ 4.66 30.5342 题解:按式 16—10,16—11 计算差数的平均值 D 与标准差 SD n D D ∑ i = =4.66/10=0.466 mg/L 1 ( ) 1 ( ) 2 2 2 − − = − − = ∑ ∑ ∑ n n D D n D D S i i i D =1.78mg/L 按式 16—12 计算 t 值 D D S D n t × = = 1.78 0.466 × 10 =0.83 查 t 分布表,当 f=9 时, t0.05,9=2.26, t<t0.05,9=2.26,说明测定结果的差别无显著性, 即两种方法的测定结果是一致的。 2、F 检验法 F 检验法是通过计算两组数据的方差之比来检验两组数据是否存在显著性差异。比如使 用不同的分析对同一试样进行测定得到的标准差不同,或几个实验室 用同一种分析方法测 定同一试样,得到的标准差不同,这时就有必要研究产生这种差异的原因,通过这种 F 检 验法,可以得到满意的解决。 F 检验法其步骤如下: (1)计算统计量方差比 2 2 2 1 S S F = 16—13 式中 2 2 2 1 S , S -分别代表两组测定值的方差 (2)查 F 分布表 (3)判断:当计算所得 F 值大于 F 分布表中相应显著性水平 α 和自由度 f1,f2 下的临界 值 fα(f1,f2),即 F>fα(f1,f2)时,则两组方差之间有显著性差异,反之,则两组方差无显著性 差异。 在编制 F 分布表时,是将大方差作分子,小方差作分母,所以,在由样本值计算统计 量 F 值时,也要将样本方差 2 2 2 1 S , S 中数值较大的一个作分子,较小的一个作分母。 例 16-10 仍以例 16-8 中实验数据为例,通过 F 检验法比较两种方法的精密度有无显著 差异。 题解:分别计算两种方法的方差 S1 2 =0.0832 =0.0069 S2 2 =0.0352 =0.0012 按式 16-13 计算统计量方差比 F:

F S2-0.006910.0012=5.75 查F分布表,Fs(5,4)=626,F<F(5,4626 说明差别不明显,即两种测定方法精密度是一致的。 例16-11用原子吸收法与比色法同时测定某试样中的铜,各进行了10次测定,原子吸 收法测定方差为65×10+,比色法测定的方差为8.0×10,试由测定精密度考虑,以选取 那一测定方法合适 题解:(1)给定量若性水平=0.10,根据本例题意,只要检验两个方差是否有显著性 差异,不管两个方差中哪一个比另一个大得多或小得多,都认为是有显著性差异,因此是双 侧检验。F分布表中给示的单侧检验F临界值,对于双尾检验,在给定显著性水平α时,要 从F分布表中查Fan值,针对本例情况,查F分布表,Foos9.93.18 (2)计算统计量得 F-80X10*65x10123 <F0059,93.08说明不能认为两法方差有显著性差异,即选用原子吸收或比色法都是可以 的 第二节实验数据处理 、分析结果的表示 食品分析项目众多,某些项目测验结果还可以用多种化学型式来表示,如硫含量,可用 S2,S02,S0,S0,2化学形式表示,它们的数值各不相同。测定结果的单位也有多种形式, 如mg/L.g/L,mg/kg.z/kg,.mg100g,百分含量(%),等等,取不同单位时显然结果的数值不同。 统计处理结果的表示方法也多种多样,如算术平均值灭,极差,标准偏差等表示测定数据 的离散程度(精密度)。 原则上讲,食品分析要求提出的测定结果既反映数据的集中趋热,又反映测定精密度及 测定次数,另外还要照顾食品分析自身的习惯表示法。 通常,食品的分析中报出的测定结果的单位采用mg%或百分含量%,而对食品中微量 无素的测定结果采用mgkg即ppm或gmg(ppb),统计处理的结果采用测定值的算术平均 数灭与相差R=Xmax-Xmin同时表示。当测定数据的重现性较好时,测定次数n通常为2 次,当测定数据的重视性较差时,分析次数应相应地增加。 二、实验数据的处理 通过测定工作获得一系列有关分析数据后,需按以下原侧记录,运算与处理。 一)记录与运算规则 食品分析中数据记录与计算均按有效数字计算法进行,即: (1)除有特殊规定外,一般可疑数为最后一位,有士1个单位的误差。 (2)复杂运算时,其中间过程可多保留一位,最后结果须取应有的位数。 (3)加减法计算结果,其小数点以后保留的位数,应与参加运算各数中小数点以后位 数最少者相同 (4)乘除法计算结果,其有效数字保留的位数,应与参加运算各数中有效数字位数最 少者相同
2 2 2 1 S S F = =0.0069/0.0012=5.75 查 F 分布表,F0.05(5,4)=6.26, F<F0.05(5,4)=6.26 说明差别不明显,即两种测定方法精密度是一致的。 例 16-11 用原子吸收法与比色法同时测定某试样中的铜,各进行了 10 次测定,原子吸 收法测定方差为 6.5×10-4,比色法测定的方差为 8.0×10-4,试由测定精密度考虑,以选取 那一测定方法合适。 题解:(1)给定量著性水平 α=0.10,根据本例题意,只要检验两个方差是否有显著性 差异,不管两个方差中哪一个比另一个大得多或小得多,都认为是有显著性差异,因此是双 侧检验。F 分布表中给示的单侧检验 F 临界值,对于双尾检验,在给定显著性水平 α 时,要 从 F 分布表中查 Fα/2 值,针对本例情况,查 F 分布表,F0.05(9,9)=3.18 (2)计算统计量得 =8.0×10-4/6.5×10-4=1.23 F<F0.05(9,9)=3.08 说明不能认为两法方差有显著性差异,即选用原子吸收或比色法都是可以 的。 第二节 实验数据处理 一、分析结果的表示 食品分析项目众多,某些项目测验结果还可以用多种化学型式来表示,如硫含量,可用 S2-,SO2,SO3,SO4 2-化学形式表示,它们的数值各不相同。测定结果的单位也有多种形式, 如 mg/L,g/L,mg/kg,g/kg,mg/100g,百分含量(%),等等,取不同单位时显然结果的数值不同。 统计处理结果的表示方法也多种多样,如算术平均值 X ,极差,标准偏差等表示测定数据 的离散程度(精密度)。 原则上讲,食品分析要求提出的测定结果既反映数据的集中趋热,又反映测定精密度及 测定次数,另外还要照顾食品分析自身的习惯表示法。 通常,食品的分析中报出的测定结果的单位采用 mg%或百分含量%,而对食品中微量 无素 的测定结果采用 mg/kg 即 ppm 或 μg/mg(ppb),统计处理的结果采用测定值的算术平均 数 X 与相差 R=Xmax-Xmin 同时表示。当测定数据的重现性较好时,测定次数 n 通常为 2 次,当测定数据的重视性较差时,分析次数应相应地增加。 二、实验数据的处理 通过测定工作获得一系列有关分析数据后,需按以下原则记录,运算与处理。 (一)记录与运算规则 食品分析中数据记录与计算均按有效数字计算法进行,即: (1)除有特殊规定外,一般可疑数为最后一位,有±1 个单位的误差。 (2)复杂运算时,其中间过程可多保留一位,最后结果须取应有的位数。 (3)加减法计算结果,其小数点以后保留的位数,应与参加运算各数中小数点以后位 数最少者相同。 (4 ) 乘除法计算结果,其有效数字保留的位数,应与参加运算各数中有效数字位数最 少者相同。 2 2 2 1 S S F =

(二)可疑数据的检验与取舍 L.实验中的可疑值 在实际分析测试中,由于随机误差的存在,使得多次重复测定的数据不可能完全一致 而 定的离散性 并且常常发现 组测定使其中某一、两个测定值比其余测定值明显的 偏大或偏小,这样的测定值称为可疑值。 可疑值可能是测定值随机流动的极度表现。它虽然明显偏离其余测定值,但仍然是处于 统计上所允许的合理误差之内,与其余测定使属于同一总体称之为极值,极值是一个好值, 必须保留,处而也有可能存在这样的情况,战是可量值与其金测定值并不屈干同一总体。称 其为界外值、异常值、坏值,应淘汰不要 对于可疑值,必须首先从技术上设法弄清楚其出现的原因。如果查明是由实验技术上的 失误引起的,不管这样的测定值是否为异常值都应舍弃,而不必进行统计检验。但是,有时 由于各种缘故未必能从技术上找出它出现过失的原因,在这种情况下,既不能轻意地保留它, 也不能随意地舍弃它,应对它进行统计检验,以便从统计上判明可疑值是否为异常值。如果 且确定为异常值 就应从这组测定中将其除掉。 2。舍弃异常值的依据 对于可疑值究竟是极值还是异常值的检验,实质上就是区分随机误差和过失误差的问 题。因为随机误差遵从正态分布的统计规律,在一组测定值中出现大偏差的概率很小的。单 欠测定值出现土2。(σ为标准差,也用S表示)之间的概率为955%(这一概率也称为置 信概幸或置信度, 2将为置信区间),也就是说偏差>26的出现概率为5%(这概率也称 之为显著概率或 性水 而偏去 ,3的棉 只有0.3% 通常分析检验只进行 少数儿次测定,按常规来说,出现大偏差测定值的可能性理应是非常小的,而现在竞然出现 了,那么就有理由将偏差很大的测定值作为与其余的测定值来源于不同的总体异常值舍弃 它。并将2c和30称为允许合理误差范围,也称为临界值。 可好估的检验准则 ①己知标准差 如果人们在长期实践中已知道了标准差。的数值,可直接用2(置信 度95.5%)或3o(置信度99.7)作为取公依据 ②未知标准差 一般情况下,总体标准差σ事先并不知道,而要由测定值本身来计算 它,并依次来检验该组测定值中是否混有异常值,判别方法有许多,如狄克逊(Dxo)检 验法,格鲁布斯(Grubbs)检验法、科克伦(Cochran)最大方差检验法等。下面介绍前两 种方法: (1)狄克逊(Dxon)检验法 此法也叫Q统计量法,是指用狄克逊法检验测定值(或平均值)的可疑值和界外值的 统计量,并以此来决定最大或最小的测定值(或平均值)的取舍。其中提到关于平均值的取 舍问题,是由于有时要进行几组数据的重复测定,取几次测定值的平均值,也有一个可疑值 取金问颗,也要讲行检哈 现将Q统计量法和检验步骤和方法说明如下 ①首先将一组测定值按大次序排列:即:X≤X,≤X一≤X1≤X不言而喻,异常值(界 外值)必然出现在两端。 ②用表16-3,所列公式,计算Q统计量。计算时,Q统计量的有效数字应保留至小数点后 3位 ③从表16一4查出检验显著概率为5%和1%的Q统计最的临界值Q05 和 0,其 中H为受检验的一组按小到大排列的测定值的最大的一个序数(也就是测定次数),从受检 测定值的两个Q统计量计算值中,只选取较大的Q统计量的计算值与Q统计量的临界值比 较
(二)可疑数据的检验与取舍 1.实验中的可疑值 在实际分析测试中,由于随机误差的存在,使得多次重复测定的数据不可能完全一致, 而存在一定的离散性,并且常常发现一组测定使其中某一、两个测定值比其余测定值明显的 偏大或偏小,这样的测定值称为可疑值。 可疑值可能是测定值随机流动的极度表现。它虽然明显偏离其余测定值,但仍然是处于 统计上所允许的合理误差之内,与其余测定使属于同一总体称之为极值,极值是一个好值, 必须保留,然而也有可能存在这样的情况,就是可疑值与其余测定值并不属于同一总体,称 其为界外值、异常值、坏值,应淘汰不要。 对于可疑值,必须首先从技术上设法弄清楚其出现的原因。如果查明是由实验技术上的 失误引起的,不管这样的测定值是否为异常值都应舍弃,而不必进行统计检验。但是,有时 由于各种缘故未必能从技术上找出它出现过失的原因,在这种情况下,既不能轻意地保留它, 也不能随意地舍弃它,应对它进行统计检验,以便从统计上判明可疑值是否为异常值。如果 一旦确定为异常值,就应从这组测定中将其除掉。 2.舍弃异常值的依据 对于可疑值究竟是极值还是异常值的检验,实质上就是区分随机误差和过失误差的问 题。因为随机误差遵从正态分布的统计规律,在一组测定值中出现大偏差的概率很小的。单 次测定值出现 μ±2σ(σ 为标准差,也用 S 表示)之间的概率为 95.5%(这一概率也称为置 信概率或置信度 μ±2σ 将为置信区间),也就是说偏差﹥2σ 的出现概率为 5%(这概率也称 之为显著概率或显著性水平);而偏差﹥3σ 的概率更小,只有 0.3%。通常分析检验只进行 少数几次测定,按常规来说,出现大偏差测定值的可能性理应是非常小的,而现在竟然出现 了,那么就有理由将偏差很大的测定值作为与其余的测定值来源于不同的总体异常值舍弃 它。并将 2σ 和 3σ 称为允许合理误差范围,也称为临界值。 3.可疑值的检验准则 ①已知标准差 如果人们在长期实践中已知道了标准差 σ 的数值,可直接用 2σ(置信 度 95.5%)或 3σ(置信度 99.7)作为取舍依据 ②未知标准差 一般情况下,总体标准差 σ 事先并不知道,而要由测定值本身来计算 它,并依次来检验该组测定值中是否混有异常值,判别方法有许多,如狄克逊(Dixon)检 验法,格鲁布斯(Grubbs)检验法、科克伦(Cochran)最大方差检验法等。下面介绍前两 种方法: (1)狄克逊(Dixon)检验法 此法也叫 Q 统计量法,是指用狄克逊法检验测定值(或平均值)的可疑值和界外值的 统计量,并以此来决定最大或最小的测定值(或平均值)的取舍。其中提到关于平均值的取 舍问题,是由于有时要进行几组数据的重复测定,取几次测定值的平均值,也有一个可疑值 取舍问题,也要进行检验。 现将 Q 统计量法和检验步骤和方法说明如下: ①首先将一组测定值按大次序排列:即:X1≤X2≤X3-≤Xn-1≤Xn不言而喻,异常值(界 外值)必然出现在两端。 ②用表 16-3,所列公式,计算 Q 统计量。计算时,Q 统计量的有效数字应保留至小数点后 3 位。 ③从表 16-4 查出检验显著概率为 5%和 1%的 Q 统计量的临界值 Q0.05,(H)和 Q0.01,(H),其 中 H 为受检验的一组按小到大排列的测定值的最大的一个序数(也就是测定次数),从受检验 的测定值的两个 Q 统计量计算值中,只选取较大的 Q 统计量的计算值与 Q 统计量的临界值比 较
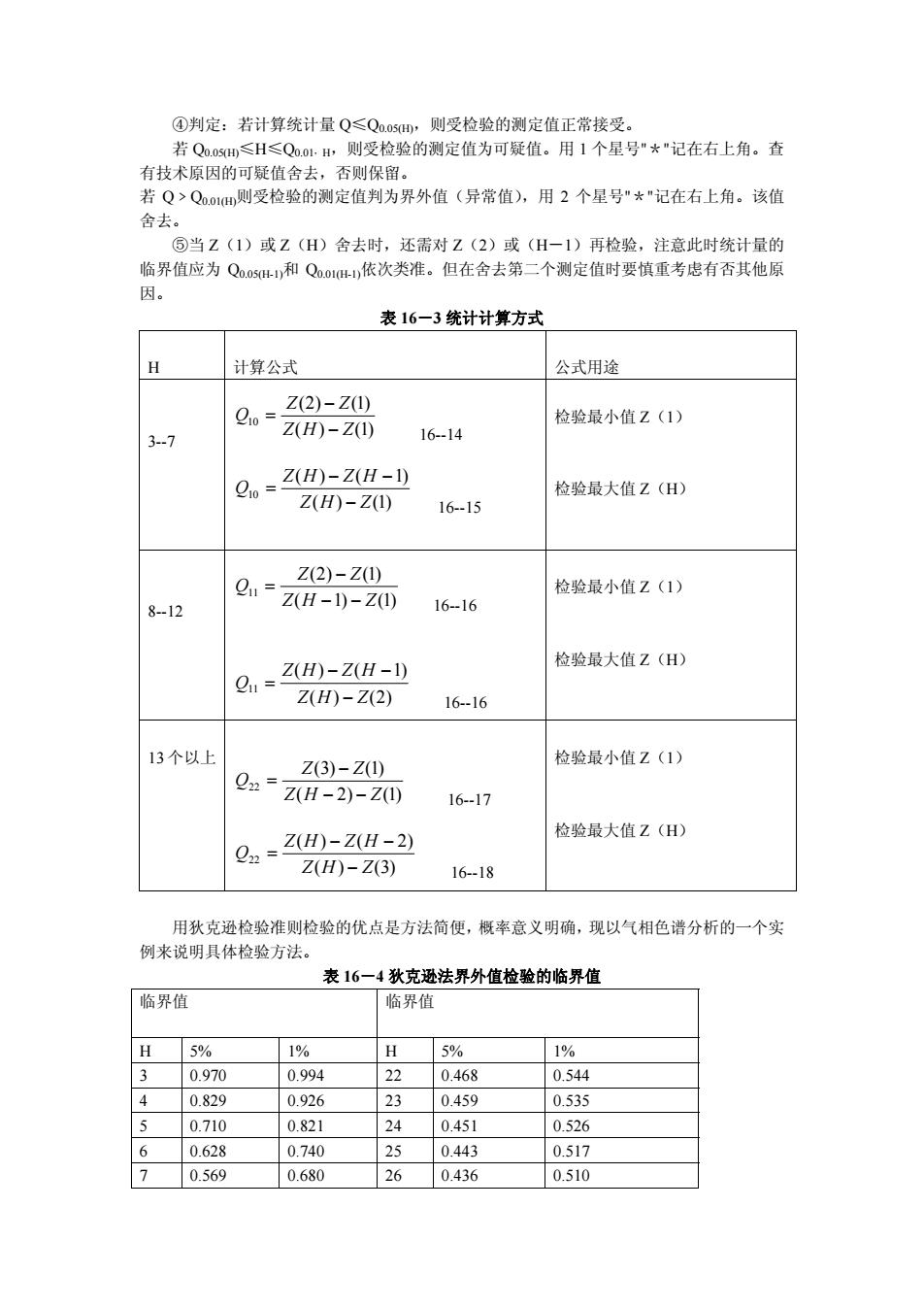
④判定:若计算统计量Q≤Q。s,则受检验的测定值正常接受。 若O 0-H 则受检验的测定值为可疑值。用1个星号”*“记在右上角。查 有技术原因的 可疑值去 否则保留 若Q>Q1m则受检验的测定值判为界外值(异常值),用2个星号·*"记在右上角。该值 舍去。 ⑤当Z(1)或Z(H)舍去时,还需对Z(2)或(H一1)再检验,注意此时统计量的 临界值应为Q05H和Qo1,依次类准。但在舍去第二个测定值时要慎重考虑有否其他原 表16-3统计计算方式 H 计算公式 公式用途 Z(2)-Z1) 检验最小值Z(1) 3.7 Z()-Z0) 16-14 Z(H)-Z(H-1) 检验最大值Z(日) Z(H)-Z(I) 16-15 2(2)-Z0) 8-12 0=zH-z0 检验最小值Z(1) 16-16 检验最大值Z(H) Z(H)-Z(2) 16-16 13个以H 检验最小值Z(1) Z(3)-Z1) 0zH-2)-z而 16.17 0=Z-2H-2) 检验最大值Z(H) Z(H)-Z(3) 16-18 用狄克逊检验准则检验的优点是方法简便,概率意义明确,现以气相色谱分析的一个实 例来说明具体检验方法。 表16一4秋克凝法界外值检验的临界值 临界值 临界值 H T5% 1% 5% 1% 3 0.970 0.994 22 0.468 0.544 4 0820 0026 73 0.459 0.535 0.710 0.821 0.451 0.526 6 0.628 0.740 12 0.443 0.517 7 0.569 0.680 26 0.436 0.510
④判定:若计算统计量 Q≤Q0.05(H),则受检验的测定值正常接受。 若 Q0.05(H)≤H≤Q0.01,H,则受检验的测定值为可疑值。用 1 个星号"*"记在右上角。查 有技术原因的可疑值舍去,否则保留。 若 Q﹥Q0.01(H)则受检验的测定值判为界外值(异常值),用 2 个星号"*"记在右上角。该值 舍去。 ⑤当 Z(1)或 Z(H)舍去时,还需对 Z(2)或(H-1)再检验,注意此时统计量的 临界值应为 Q0.05(H-1)和 Q0.01(H-1)依次类准。但在舍去第二个测定值时要慎重考虑有否其他原 因。 表 16-3 统计计算方式 H 计算公式 公式用途 3-7 ( ) (1) (2) (1) 10 Z H Z Z Z Q − − = 16-14 ( ) (1) ( ) ( 1) 10 Z H Z Z H Z H Q − − − = 16-15 检验最小值 Z(1) 检验最大值 Z(H) 8-12 ( 1) (1) (2) (1) 11 Z H Z Z Z Q − − − = 16-16 ( ) (2) ( ) ( 1) 11 Z H Z Z H Z H Q − − − = 16-16 检验最小值 Z(1) 检验最大值 Z(H) 13 个以上 ( 2) (1) (3) (1) 22 Z H Z Z Z Q − − − = 16-17 ( ) (3) ( ) ( 2) 22 Z H Z Z H Z H Q − − − = 16-18 检验最小值 Z(1) 检验最大值 Z(H) 用狄克逊检验准则检验的优点是方法简便,概率意义明确,现以气相色谱分析的一个实 例来说明具体检验方法。 表 16-4 狄克逊法界外值检验的临界值 临界值 临界值 H 5% 1% H 5% 1% 3 0.970 0.994 22 0.468 0.544 4 0.829 0.926 23 0.459 0.535 5 0.710 0.821 24 0.451 0.526 6 0.628 0.740 25 0.443 0.517 7 0.569 0.680 26 0.436 0.510