
第四章 常用概率分布 第一节正态分布 一、正态分布的概念 正态分布是自然界最常见的一种分布,若指标 X的频率分布曲线对应于数学上的正态分布曲线 则称该指标服从正态分布
一、正态分布的概念 第四章 常用概率分布 第一节 正态分布 正态分布是自然界最常见的一种分布,若指标 X的频率分布曲线对应于数学上的正态分布曲线, 则称该指标服从正态分布
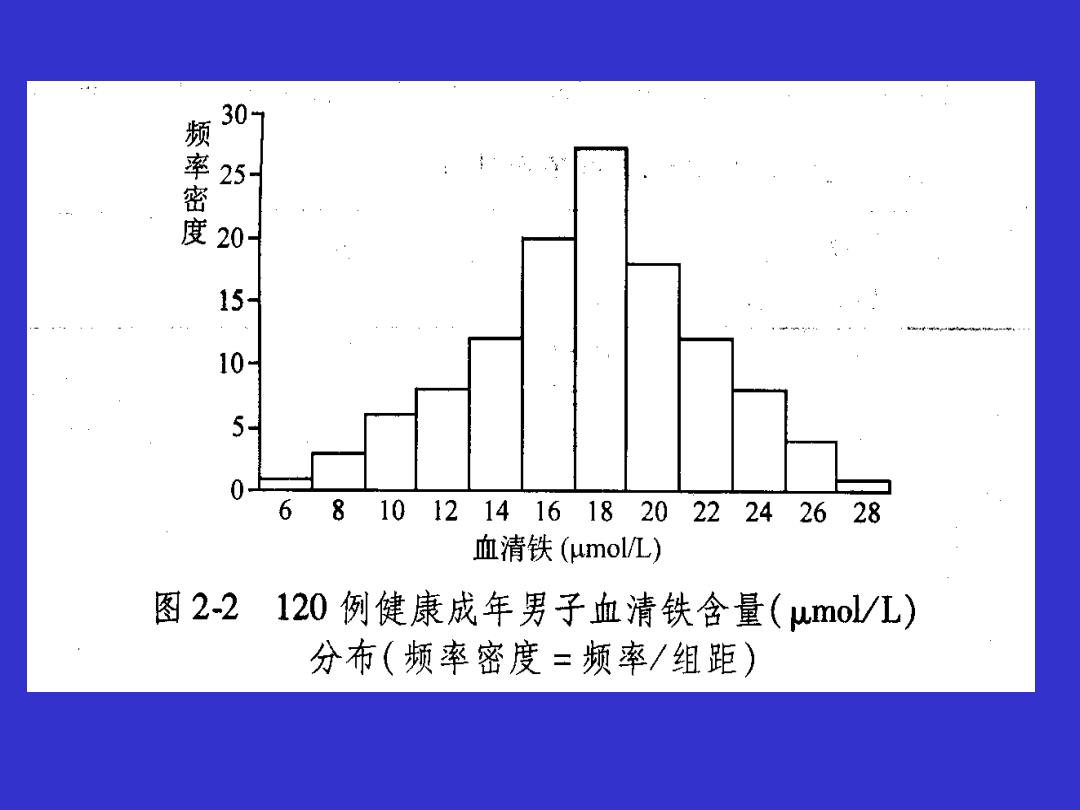
频率密度 5 0 5- 0 6810121416 182022242628 血清铁(μmolL) 图2-2 120例健康成年男子血清铁含量(umol/L) 分布(频率密度=频率/组距)

20 15 10 0 109 113 117121 125 129 133 10 & 6 4 2 0 105 109 113 117 121125 129 133 107109111113115117119121123125127129131133 图3.1频数分布逐渐接近正态分布示意图

正态分布的密度函数,即正态曲线的方程为 -00<X<≤+00 b.均数相同、标准差不同(o1<o2<σ3)的三条正态曲线 图4-5正态曲线位置、形状与u、σ关系示意图
正态分布的密度函数,即正态曲线的方程为 -∞<X<+∞

均数为0,标准差为1的正态分布,这种正态分布 称为标准正态分布。 对于任意一个服从正态分布N(μ,σ)的随机变量 可作如下的标准化变换,也称Z变换,(教材57) Z= X-4 标准正态分布的密度函数: -00<Z<+0 (亿)为标准正态分布的密度函数,即纵坐标的高度
均数为0,标准差为1的正态分布,这种正态分布 称为标准正态分布。 -∞<Z<+∞ 标准正态分布的密度函数: 为标准正态分布的密度函数,即纵坐标的高度。 对于任意一个服从正态分布N(μ,σ2)的随机变量, 可作如下的标准化变换,也称Z变换,(教材57) − = X Z

(二)、正态分布的特征 1.关于x=4对称。即正态分布以均数为中 心,左右对称。 2.在X= 处取得概率密度函数的最大值, 在飞二!士可处有拐点,表现为钟形曲线。即正 态曲线在横轴上方均数处最高
(二)、正态分布的特征 1. 关于 对称。即正态分布以均数为中 心,左右对称。 2. 在 处取得概率密度函数的最大值, 在 处有拐点,表现为 钟形曲线。即正 态曲线在横轴上方均数处最高

3.正态分布有两个参数,即均数和标准差σ。 是位置参数,σ是变异度参数(形状参数)。常用 N(,σ2)表示均数为μ,标准差为o的正态分布;用 N(0,1)表示标准正态分布。 4.正态曲线下面积分布有一定规律。横轴上 正态曲线下的面积等于100%或1
3. 正态分布有两个参数,即均数µ和标准差σ。 µ是位置参数,σ是变异度参数(形状参数)。常用 N(µ,σ2 )表示均数为μ ,标准差为σ的正态分布;用 N(0,1)表示标准正态分布。 4. 正态曲线下面积分布有一定规律。横轴上 正态曲线下的面积等于100%或1

二、正态曲线下面积的分布规律 正态方程的积分式(分布函数): F) dX FX)为正态变量X的累计分布函数,反映正态曲线下,横 轴尺度自一∞到X的面积,即下侧累计面积 标准正态分布方程积分式(分布函数): e 2 dZ 2元 Φ(Z)为标准正态变量z的累计分布函数,反映标准正态曲 线下,横轴尺度自一∞到Z的面积,即下侧累计面积
二、正态曲线下面积的分布规律 正态方程的积分式(分布函数): F(X)为正态变量X的累计分布函数,反映正态曲线下,横 轴尺度自-∞到X的面积,即下侧累计面积 。 标准正态分布方程积分式(分布函数): Φ(Z)为标准正态变量z的累计分布函数,反映标准正态曲 线下,横轴尺度自-∞到Z的面积,即下侧累计面积
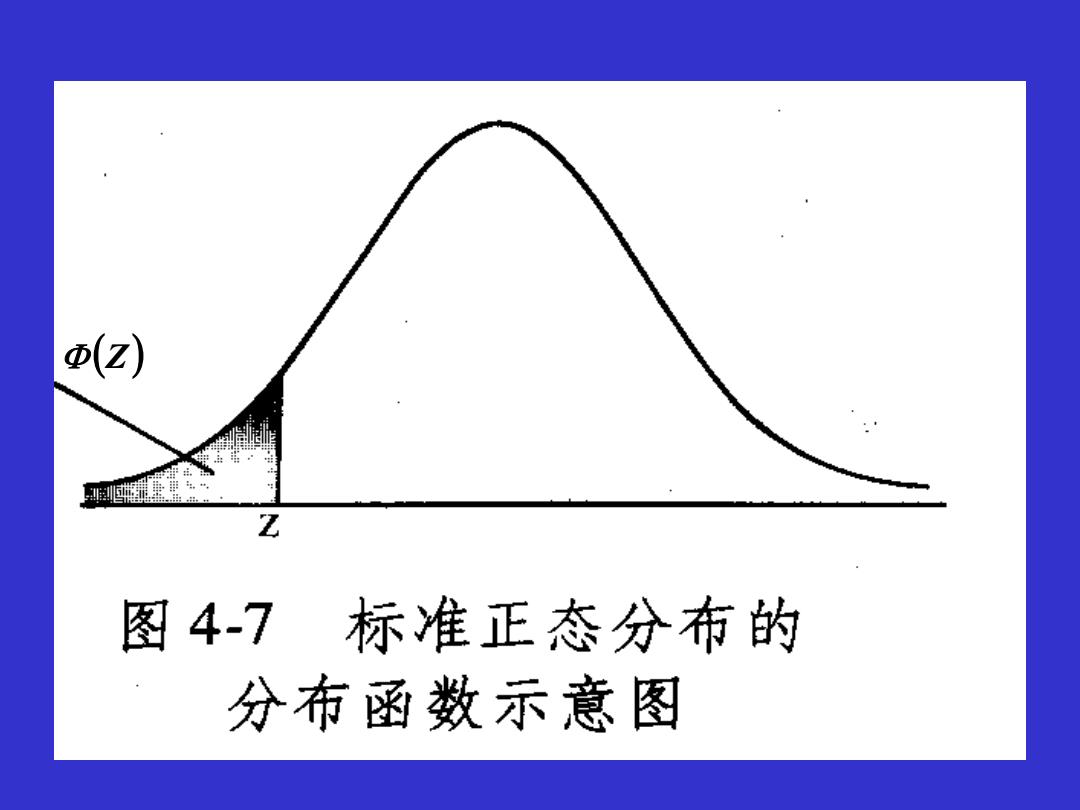
(z) Z 图4-7标准正态分布的 分布函数示意图
(Z)

三、标准正态分布表 在实际工作中为了方便用查表代替计算 1)表中曲线下面积为一∞到Z的面积。 2)当山,σ和X已知时,先求出Z值, z=-) 再用Z值查表,得所求区间占总面积的比例。 当和σ未知时,要用样本均数和样本标准差S来估计Z值。 (X-x 3)曲线下对称于0的区间,面积相等。 4)曲线下横轴上的面积为100%或1
在实际工作中为了方便用查表代替计算 1)表中曲线下面积为-∞到Z的面积。 2)当µ,σ和X已知时,先求出Z值, 再用Z值查表,得所求区间占总面积的比例。 当µ和σ未知时,要用样本均数和样本标准差S来估计Z值。 3)曲线下对称于0的区间,面积相等。 4)曲线下横轴上的面积为100%或1。 ( ) − = X Z ( ) S X X Z − = 三、标准正态分布表