
第十一章 两变量关联性分析 前面章节中讲述了单一数值变量的统计 分析方法,但在医学科学研究中常要分析变 量间的关系,如年龄与血压、药物剂量和动 物死亡率、环境介质中污染物浓度与污染 源距离等,回归与相关就是研究这种关系 的统计方法,属于双变量分析范畴。 第一节 线性相关
第十一章 两变量关联性分析 前面章节中讲述了单一数值变量的统计 分析方法,但在医学科学研究中,常要分析变 量间的关系,如年龄与血压、药物剂量和动 物死亡率、环境介质中污染物浓度与污染 源距离等,回归与相关就是研究这种关系 的统计方法,属于双变量分析范畴。 第一节 线性相关

直线相关的概念及其统计描述 例11-1随机抽取15名健康成人,测 定血液的凝血酶浓度(单位/毫升)及凝固时 间(秒),数据如表11-1所示。 据此资料 如何判断这两项指标间有否相关? 表11-115名健康成人凝血时间与凝血酶浓度测量值记录 受试者号 3 4 67 8910 111213 14 15 凝血酶浓度 1.11.21.00.9 1.2 1.10.9 0.61.0 0.91.1 0.9 1.1 1.0 0.7 凝血时间 1413151513141617141615161415 17
一、直线相关的概念及其统计描述 例11-1 随机抽取15名健康成人,测 定血液的凝血酶浓度(单位/毫升)及凝固时 间(秒),数据如表11-1所示。据此资料 如何判断这两项指标间有否相关? 表11-1 15名健康成人凝血时间与凝血酶浓度测量值记录 受试者号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 凝血酶浓度 1.1 1.2 1.0 0.9 1.2 1.1 0.9 0.6 1.0 0.9 1.1 0.9 1.1 1.0 0.7 凝血时间 14 13 15 15 13 14 16 17 14 16 15 16 14 15 17
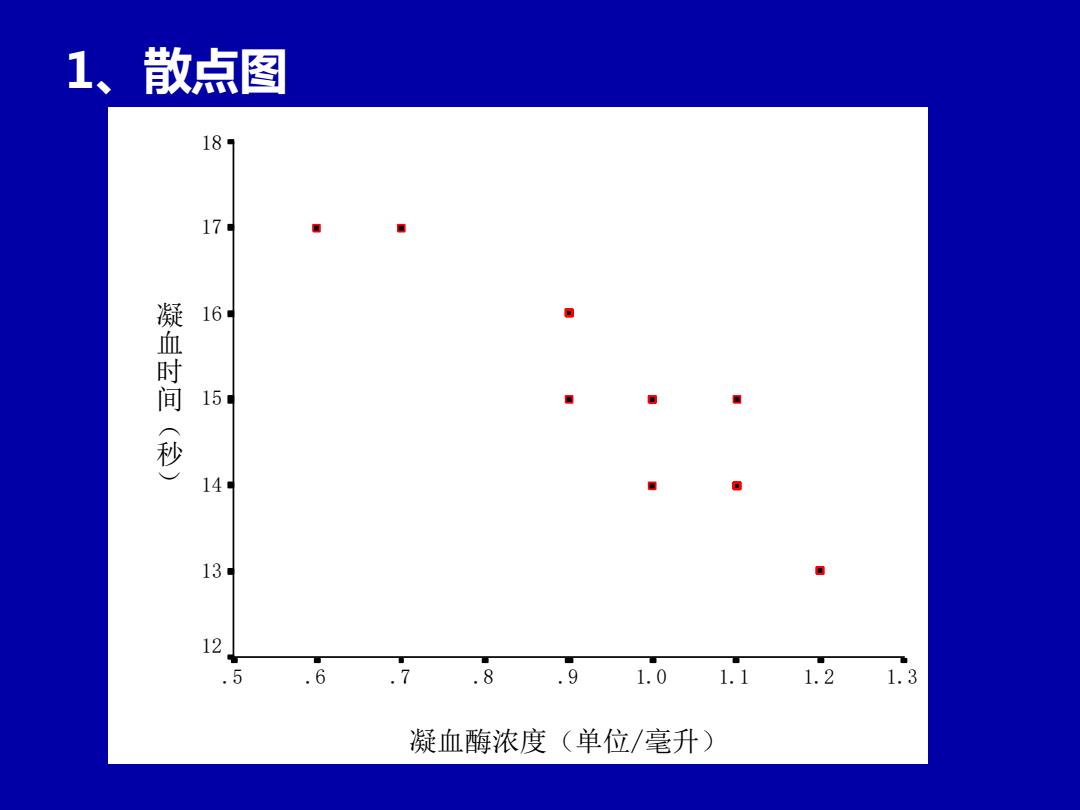
1、散点图 181 17 16 国 凝血时间 15 秒) 14 13 12 .5 .6 .7.8.9 1.0 1.1 1.21.3 凝血酶浓度(单位/毫升)
1、散点图 凝血酶浓度(单位/毫升) .5 .6 .7 .8 .9 1.0 1.1 1.2 1.3 凝 血 时 间 ( 秒 ) 18 17 16 15 14 13 12
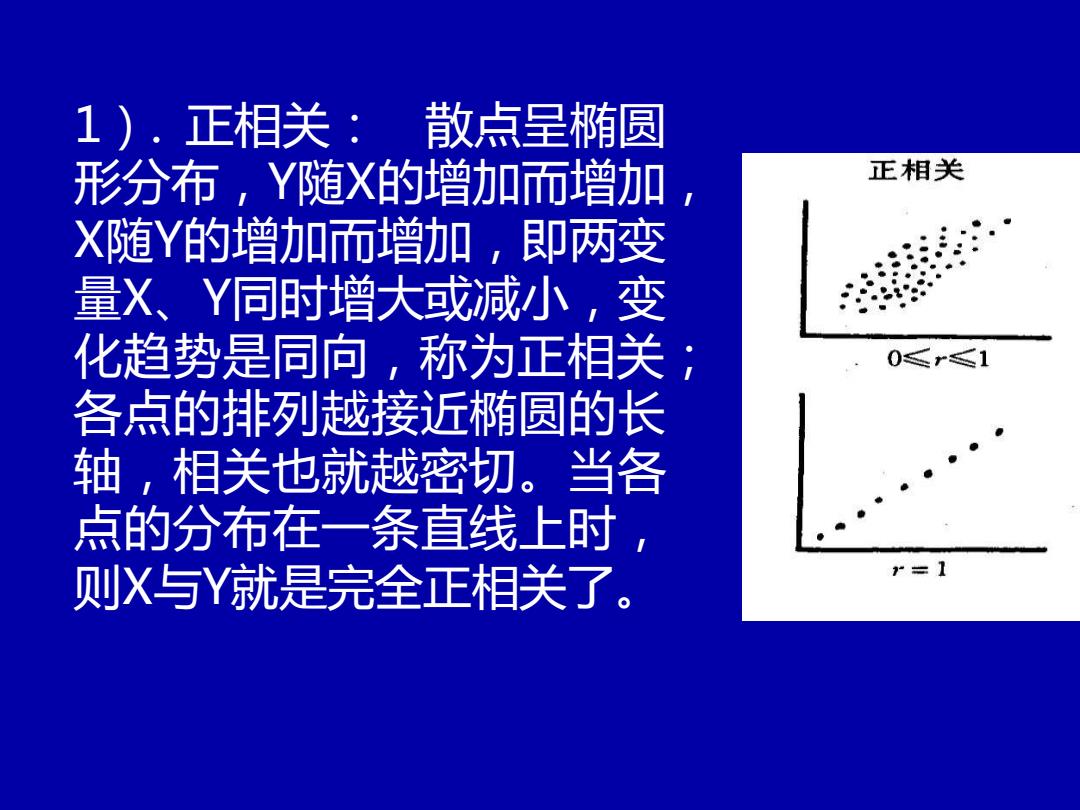
1).正相关:散点呈椭圆 形分布,Y随X的增加而增加 正相关 X随Y的增加而增加,即两变 量X、Y同时增大或减小,变 化趋势是同向,称为正相关 ≤r1 各点的排列越接近椭圆的长 轴,相关也就越密切。当各 点的分布在一条直线上时 则X与Y就是完全正相关了。 r=1
1). 正相关: 散点呈椭圆 形分布,Y随X的增加而增加, X随Y的增加而增加,即两变 量X、Y同时增大或减小,变 化趋势是同向,称为正相关; 各点的排列越接近椭圆的长 轴,相关也就越密切。当各 点的分布在一条直线上时, 则X与Y就是完全正相关了
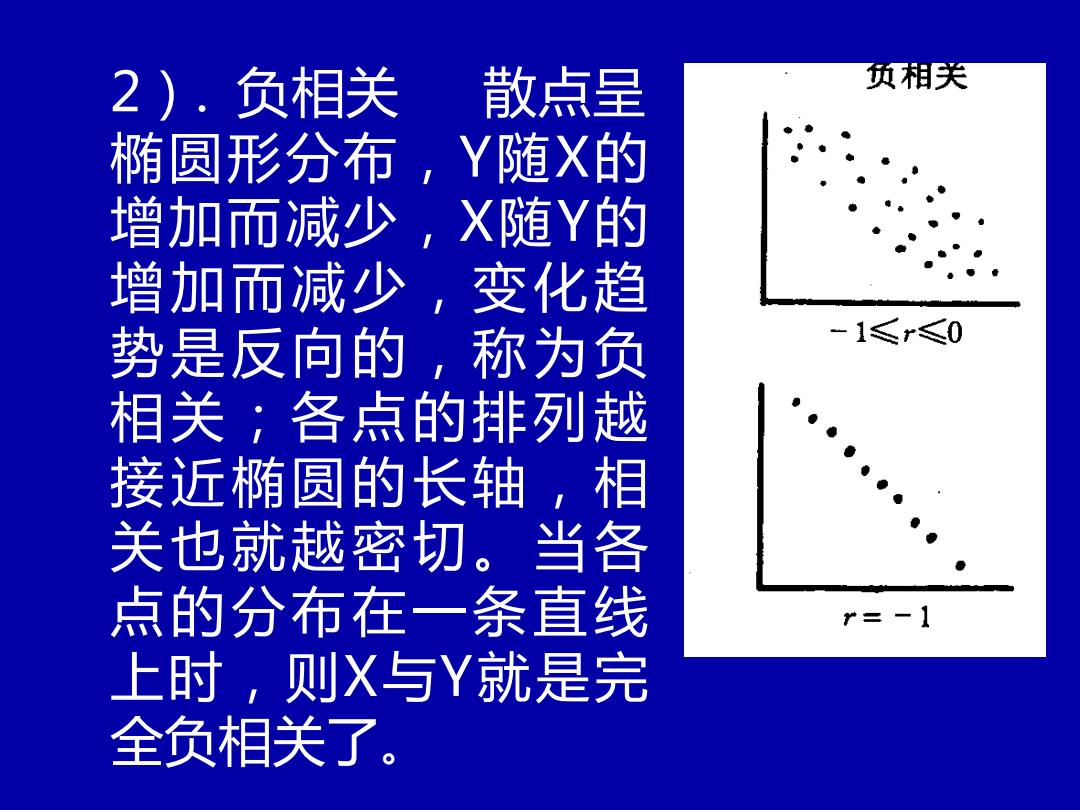
2).负相关 散点呈 预相关 椭圆形分布,Y随X的 增加而减少,X随Y的 增加而减少,变化趋 势是反向的, 称为负 -1≤r≤0 相关;各点的排列越 接近椭圆的长轴, 相 关也就越密切。当各 点的分布在一条直线 r=-1 上时,则X与Y就是完 全负相关了
2). 负相关 散点呈 椭圆形分布,Y随X的 增加而减少,X随Y的 增加而减少,变化趋 势是反向的,称为负 相关;各点的排列越 接近椭圆的长轴,相 关也就越密切。当各 点的分布在一条直线 上时,则X与Y就是完 全负相关了
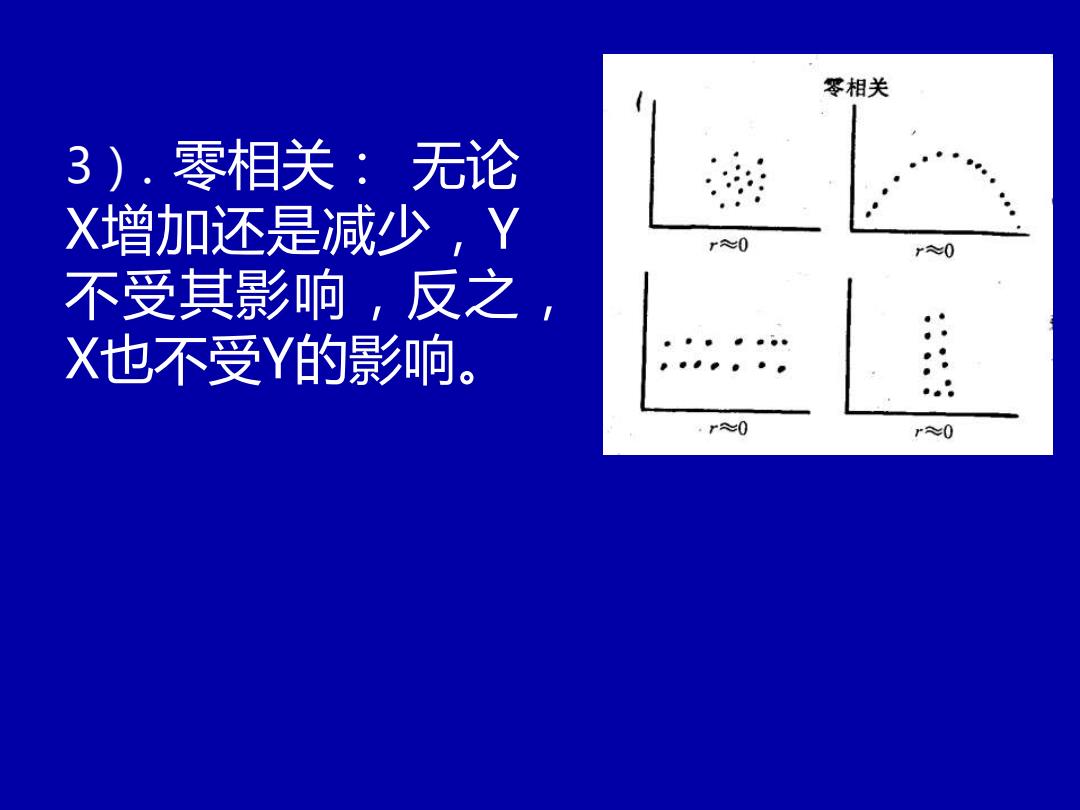
零相关 3).零相关:无论 X增加还是减少,Y r≈0 r≈0 不受其影响,反之 X也不受Y的影响。 r≈0 r≈0
3). 零相关: 无论 X增加还是减少,Y 不受其影响,反之, X也不受Y的影响

2、相关系数 它又称为积差相关系数,以符号r来表 示相关系数: 它是说明两变量间相关关系的密切程度 和相关方向。 X和Y的协方差 相关系数= √(区的方差Y的方差
2、相关系数 它又称为积差相关系数,以符号r 来表 示相关系数。 它是说明两变量间相关关系的密切程度 和相关方向。 ( 的方差)( 的方差) 和 的协方差 相关系数= X Y X Y

现在我们来解释协方差(covariance) 的含义。当样本值为(x1y1),(X2y2)· (xyn)时,x和Y的样本均数分别为和 Σ-) Σ6-列 X的样本方差= y的样本方差 n-1 n-1 ∑(-x0-) X和Y的样本协方差 n-1 ∑(x-y-)
现在我们来解释协方差(covariance) 的含义。当样本值为(x1 ,y1 ), (x2 ,y2 ),… (xn ,yn )时,x和Y的样本均数分别为 ( ) 1 X − − = n x x n 的样本方差 i x和y ( ) 1 y − − = n y y n 的样本方差 i ( )( ) 1 X Y − − − = n x x y y n 和 的样本协方差 i

例11一2 计算例11一1中凝血酶浓度与凝血时间 之间的样本相关系数 由原始出立x=14,7∑x=1481=15 ∑=24∑7=36∑x=2167 216.7-14.7X224 15 481-4.7755368-24735 -2.82 =-0.926 √0.404V22.933

二、 相关系数的假设检验 是样本相关系数,它是总体相关系 数的估计值。要判断X、Y间是否有相关 关系,就要检验是否来自总体相关系数p 为零的总体 对相关系数的假设检验方法有两种: 1、查表法 2、采用t检验 检验统计量为: ,V=n-2 n-2
二、相关系数的假设检验 r是样本相关系数,它是总体相关系 数 的估计值。要判断X、Y间是否 有相关 关系,就要检验r是否来自总体相关系数 为零的总体。 对相关系数的假设检验方法有两种: 1、查表法 2、采用t检验 检验统计量为: